DFS 之 全排列

Posted 2020-08-10 qlyc

题目描述
输出自然数1到n所有不重复的排列，即n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

我们可以模拟出n个盒子和n张卡片，我们需要将n张卡片分别放到n个盒子里，且每个盒子只能放1张卡片，那有多少种方案呢？

我们来模拟一下放卡片。

 

 

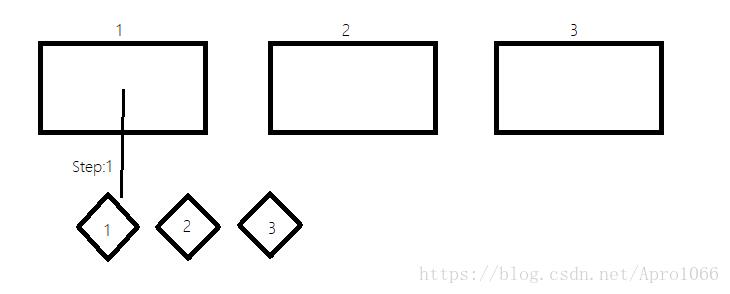
现在放了第1张卡片，接下来亦是如此。

 

产生排列"1 2 3"。

经过综上，已经完成了一种排列。那是不是就结束了呢？显然不是！因为产生了一种排列后需要立即返回，现在我们要把第3张卡片收回。

 

取回了第3张卡片后，发现手里仍然只有第3张卡片，没有别的选择，于是不得不把2号卡片收回。

 

现在手里有2张卡片了，分别是2、3号卡片。现在需要把3号卡片放入第2个盒子里，放好后再把2号卡片放到3号盒子里，产生排列"1 3 2"。

接下来按照上面的程序去模拟，会依次生成所有排列"2 1 3"、"2 3 1"、"3 1 2"、"3 2 1"。

这个模拟的过程，就是dfs的基本操作。

现在请出代码。

考虑2个情况：1是如何往盒子里放卡片，2是放过的卡片就不能放到其他盒子里了，因为一个盒子只能放1个卡片。这里1个for循环和标记判断就能搞定。

for(i=1;i<=n;i++)//从1到n个盒子产生排列 
{
    if(b[i]==0)//如果卡片在手上，b[i]==0表示第i号卡片在手上 
    {
        a[step]=i;//将第i个卡片放入第step个盒子里 
        b[i]=1;//标记第i号卡片不在手上 
    }
}

这里a数组是表示小盒子，b数组是标记卡片是否在手上。step表示正处在第step个盒子上。

OK，现在已经处理掉第step个盒子了，接下来往深处走，处理第step+1个盒子。如何处理step+1个盒子呢？其实和处理第step个盒子是一样的。显然我们需要把刚才处理第step个盒子封装成函数。

inline void dfs(int step)//处理第step个盒子 
{
    for(i=1;i<=n;i++)//从1到n个盒子产生排列 
    {
        if(b[i]==0)//如果卡片在手上，b[i]==0表示第i号卡片在手上 
        {
            a[step]=i;//将第i个卡片放入第step个盒子里 
            b[i]=1;//标记第i号卡片不在手上 
        }
    }
    return;
}

好，写成函数就好办了，在处理完第step个盒子后，就要处理第step+1个盒子，方法就是dfs(step+1)。

inline void dfs(int step)//处理第step个盒子 
{
    for(i=1;i<=n;i++)//从1到n个盒子产生排列 
    {
        if(b[i]==0)//如果卡片在手上，b[i]==0表示第i号卡片在手上 
        {
            a[step]=i;//将第i个卡片放入第step个盒子里 
            b[i]=1;//标记第i号卡片不在手上
            dfs(step+1);//通过递归实现处理下一个盒子
            b[i]=0;//一定要把刚才尝试的卡片收回，才能进行下一次尝试 
        }
    }
    return;
}

上面b[i]=0十分重要，因为在一次摆放尝试结束返回时，如果不把刚才的卡片收回，那将无法进行下一次摆放。

还有一个问题，什么时候才能输出一个满足要求的序列呢？我们再回到那张模拟图。

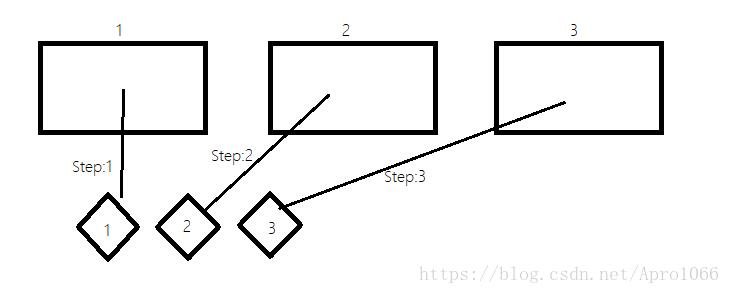
由图可知，当满足条件时应该就是卡片全部都在盒子里。当我们要处理第n+1个盒子时，说明前n个盒子都已经放好卡片了。

inline void dfs(int step)//处理第step个盒子 
{
    if(step==n+1)//如果前面n个盒子已经排列好 
    {
        for(i=1;i<=n;i++)//输出 
        {
            cout<<a[i]<<\' \';
        }
        cout<<endl;
        return;//非常重要！返回之前一步，也就是最近调用一次dfs的地方，否则程序将无止境地调用下去 
    } 
    for(i=1;i<=n;i++)//从1到n个盒子产生排列 
    {
        if(b[i]==0)//如果卡片在手上，b[i]==0表示第i号卡片在手上 
        {
            a[step]=i;//将第i个卡片放入第step个盒子里 
            b[i]=1;//标记第i号卡片不在手上
            dfs(step+1);//通过递归实现处理下一个盒子
            b[i]=0;//一定要把刚才尝试的卡片收回，才能进行下一次尝试 
        }
    }
    return;
}

完整代码如下：

#include <stdio.h>
#include <iostream>
using namespace std;
int a[101],b[101],n;
void print()
{
    int i;
    for(i=1;i<=n;i++)
    {
        cout<<a[i]<<\' \';
    }
    cout<<endl;
}
inline void dfs(int i)//现在是第i层，也可以看成是第i个盒子，把数据放到这个盒子里 
{
    int j;
    if(i==n+1)//如果到达了第n+1层说明已经搜索完成，输出 
    {
        print();//输出方案
        return;//返回上一层（上一个盒子）
    }
    for(j=1;j<=n;j++)//开始放数据 
    {
        if(b[j]==0)//这个数可以放（未标记） 
        {
            a[i]=j;//放这个数 
            b[j]=1;//标记被放过了 
            dfs(i+1);//放第i+1个盒子（层） 
            b[j]=0;//返回之前一步，回溯 
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    dfs(1);//开始深搜 
    return 0;
}

 

通过一个例子我们发现，dfs也就那回事。还是开头那句话：理解深搜的重要关键点是在于解决“现在该怎么做”。至于“接下来该怎么做”和“现在该怎么做”是一样的（这在骗分中十分重要）。比如上述程序的dfs(step)就是当你在第step个盒子前你应该怎么做。通常应该用循环把每一种可能都试一遍，当这步解决后就处理下一步[dfs(step+1)]。

下面是dfs的模版。

inline void dfs(int step)
{
    判断边界
    开始尝试每一种可能
    {
        ...
        dfs(step+1);//继续下一步 
    } 
    return;//返回 
}