用 Basic Mode 的计算器算对数

Posted 2020-07-26 假如你是李华

像这种常见的「普通」计算器，其实啥都能算（有了极限，啥玩意都能变成加减乘除）。其中，自然对数尤其好算，本文将提供一种方法，主要利用的是计算器的开平方功能。

---

众所周知，自然对数有如下展开式：

\\( ln{(1+x)} = x-\\frac{x^{2}}{2}+\\frac{x^{3}}{3}-\\frac{x^{4}}{4}+\\cdots \\;\\; \\left ( |x| < 1 \\right ) \\)

但这玩意对于这种「普通」计算器来说太难算了。所以，条条大路通罗马，在这里我们换一种思路。

回想一下函数 \\( y = a^x (a> 0, a \\neq 1) \\) 的导数是怎么推出来的：

\\( \\frac{\\mathrm{d}}{\\mathrm{d}x}a^x \\)

\\( =\\lim_{\\Delta x\\rightarrow 0}\\frac{a^{x+ \\Delta x} - a^x}{\\Delta x} \\)

\\( =\\lim_{\\Delta x\\rightarrow 0}a^x\\frac{a^{\\Delta x} - 1}{\\Delta x} \\)

\\( =a^x\\lim_{\\Delta x\\rightarrow 0}\\frac{a^{\\Delta x} - 1}{\\Delta x} \\) (1)

可以看出，后面那一坨极限已经跟 \\(x\\) 没关系了，应该等于一个跟 \\(a\\) 有关的常数。那么这个常数到底是多少呢？容易发现，令 \\( x=0 \\) 可得

\\( \\frac{\\mathrm{d}}{\\mathrm{d}x}a^x \\Big|_{x=0} =\\lim_{\\Delta x\\rightarrow 0}\\frac{a^{\\Delta x} - 1}{\\Delta x} \\)

也就是说，这个极限就等于函数在 \\(x=0\\) 处的导数值。根据指数函数的图像，我们「猜测」（这里就不是很严谨了，不过这不是本文的重点）当 \\(a\\) 取到某个值时，\\(x=0\\)处的切线斜率等于 \\(1\\), 即这个极限等于 \\(1\\), 此时函数的导函数恒等于函数本身。设这个值为 \\(e\\)（用 \\(ln{x}\\) 表示以 \\(e\\) 为底 \\(x\\) 的对数），可得

\\( \\frac{\\mathrm{d} }{\\mathrm{d} x} e^x = e^x \\)

所以

\\( \\frac{\\mathrm{d} }{\\mathrm{d} x} a^x \\)

\\(= \\frac{\\mathrm{d} }{\\mathrm{d} x} (e^{ln{a}})^x\\) （代入对数恒等式可得）

\\(= \\frac{\\mathrm{d} }{\\mathrm{d} x} e^{xln{a}} \\)

\\( = \\frac{\\mathrm{d} }{\\mathrm{d} (xln{a})} e^{xln{a}} \\frac{\\mathrm{d} }{\\mathrm{d} x}(xln{a}) \\) （链式法则）

\\( = e^{xln{a}}\\cdot ln{a} \\)

\\( = {(e^{ln{a}})}^x\\cdot ln{a} \\)

\\( = a^x\\cdot ln{a} \\)

跟 (1) 式比较一下，即得

\\( ln{a} = \\lim_{\\Delta x\\rightarrow 0}\\frac{a^{\\Delta x} - 1}{\\Delta x} \\) (2)

---

那么，这个 \\(e\\) 到底等于多少呢？取反函数，得：

\\( e^x = \\lim_{p\\rightarrow +\\infty }{(\\frac{x}{p}+1)}^{p} \\)

\\( e = \\lim_{p\\rightarrow +\\infty }{(\\frac{1}{p}+1)}^{p} \\)

可以算出 \\(e = 2.71828\\cdots\\), 这即是「自然对数的底」，\\( ln{x} \\) 即 \\(x\\) 的「自然对数」。

---

 (2) 式左边是对数，右边是幂，离目标近了一步，不过还是不好算。来点黑科技，把指数式变成根式：

 \\( ln{a} = \\lim_{x\\rightarrow 0}\\frac{a^{x} - 1}{x} \\)

\\( = \\lim_{k\\rightarrow +\\infty }\\frac{a^{(2^{-k})} - 1}{(2^{-k})} \\)

\\( = \\lim_{k\\rightarrow +\\infty }(a^{\\frac{1}{2^{k}} } - 1)\\cdot 2^{k} \\)

\\( = \\lim_{k\\rightarrow +\\infty }(\\sqrt[2^k]{a} - 1)\\cdot 2^{k} \\)

\\( = \\lim_{k\\rightarrow +\\infty }(\\underbrace{\\sqrt{\\cdots\\sqrt{\\sqrt{a}}}}_{k\\times } - 1)\\cdot 2^{k} \\) \\( (k\\in \\mathbb{N}) \\)

这个式子的值就很好算了，只要不断开平方就行了。试着令 \\(k=8\\), 算一下 \\( ln{2} \\):

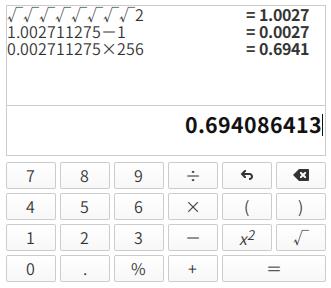
算出的值是 \\( 0.694086413 \\), 事实上 \\( ln{2} \\approx 0.693147 \\), 误差 \\( 0.000939413 \\), 怎么样，够精确吧？再算算 \\( ln{3} \\):

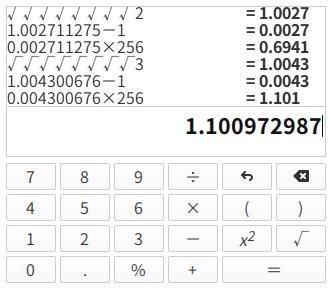
算出的值是 \\( 1.100972987 \\), 事实上 \\( ln{3} \\approx 1.09861 \\), 误差 \\( 0.00236299 \\), 比刚才略大。可以证明，\\( x \\) 越接近 \\( 1 \\), 用这种方法算出的 \\( ln{x} \\) 的近似值跟实际值误差越小。下面是函数 \\( y=ln{x} \\) 和 \\( y=(\\sqrt[256]{x}-1)\\cdot 256 \\) 在同一坐标系内的部分图像。可以看出，拟合得非常好，简直以假乱真：

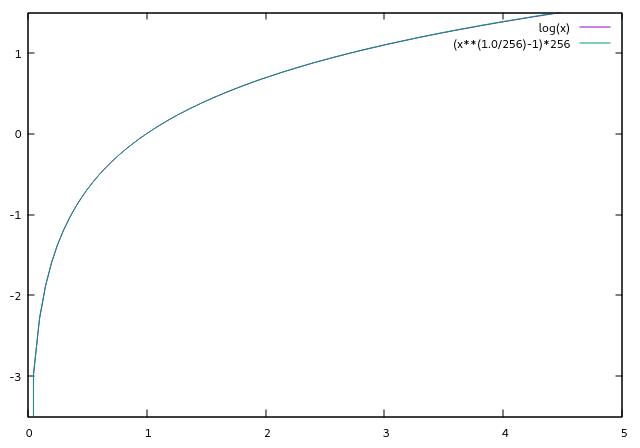
这还只是 \\( k=8 \\) 时的情形, \\(k\\) 更大就更精确了。怎么样，这个方法不错吧？