算法打靶问题求解

Posted 2020-06-12

问题描写叙述：打一枪可能的环数为0~10，求打10枪总环数为90的概率。

这是一道排列组合问题。能够用循环加递归的方法解决。

比方，第一次能够打出0~10环，那么先固定第一次打的环数。然后加上剩下的九次打的环数。就得到总环数。而剩下九次的环数通过递归非常easy求得。代码例如以下：

#include <iostream>

using namespace std;

int cnt = 0;
int target = 90;

void Permutation(int *numbers, int index, int length)
{
	if (index == length)
	{
		int sum = 0;
		for (int i = 0; i < length; i++)
			sum += numbers[i];
		
		if (sum == target)
			cnt++;
	}
	else
	{
		for (int i = 0; i <= 10; i++)
		{
			numbers[index] = i;	// 第index枪环数为i
			Permutation(numbers, index + 1, length);
		}
	}
}


int main()
{
	int numbers[10] = {0};

	Permutation(numbers, 0, 10);
	cout << (cnt / pow(11, 10)) * 100 << endl;

	system("pause");
	return 0;
}

执行这个程序，过了N久都没出结果，悲剧了。。。上面的代码相当于有10层嵌套循环。效率可想而知。

有没有优化的办法呢？事实上是有的。

在下列两种情况下。递归能够提前返回的：

1. 以打环数大于目标环数90
2. 即使剩下的每一枪都打10环也达不到90环

依据上面两种情况，我对代码进行优化：

#include <iostream>

using namespace std;

int cnt = 0;
int target = 90;

void Permutation(int *numbers, int index, int length)
{
	int PartSum = 0;	// 已有环数
	int Left = 0;		// 还须要多少环才干达到90
	for (int i = 0; i < index; i++)
		PartSum += numbers[i];
	Left = target - PartSum;
	if (PartSum > target || (length - index) * 10 < Left)
		return;

	if (index == length)
	{
		int sum = 0;
		for (int i = 0; i < length; i++)
			sum += numbers[i];
		
		if (sum == target)
			cnt++;
	}
	else
	{
		for (int i = 0; i <= 10; i++)
		{
			numbers[index] = i;	// 第index枪环数为i
			Permutation(numbers, index + 1, length);
		}
	}
}


int main()
{
	int numbers[10] = {0};

	Permutation(numbers, 0, 10);
	cout << (cnt / pow(11, 10)) * 100 << endl;

	system("pause");
	return 0;
}

执行结果：

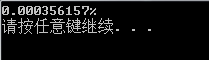
最终出结果了。经过优化后的代码。效率不知道高到哪里去了！

这个问题和八皇后问题很相似。先求出全部的情况，然后剔除不符合要求的情况或者记录符合要求的情况。