HDOJ-ACM1015(JAVA) 运用 组合全排列实现
Posted xiezie
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HDOJ-ACM1015(JAVA) 运用 组合全排列实现相关的知识,希望对你有一定的参考价值。
转载声明:原文转自:http://www.cnblogs.com/xiezie/p/5573934.html
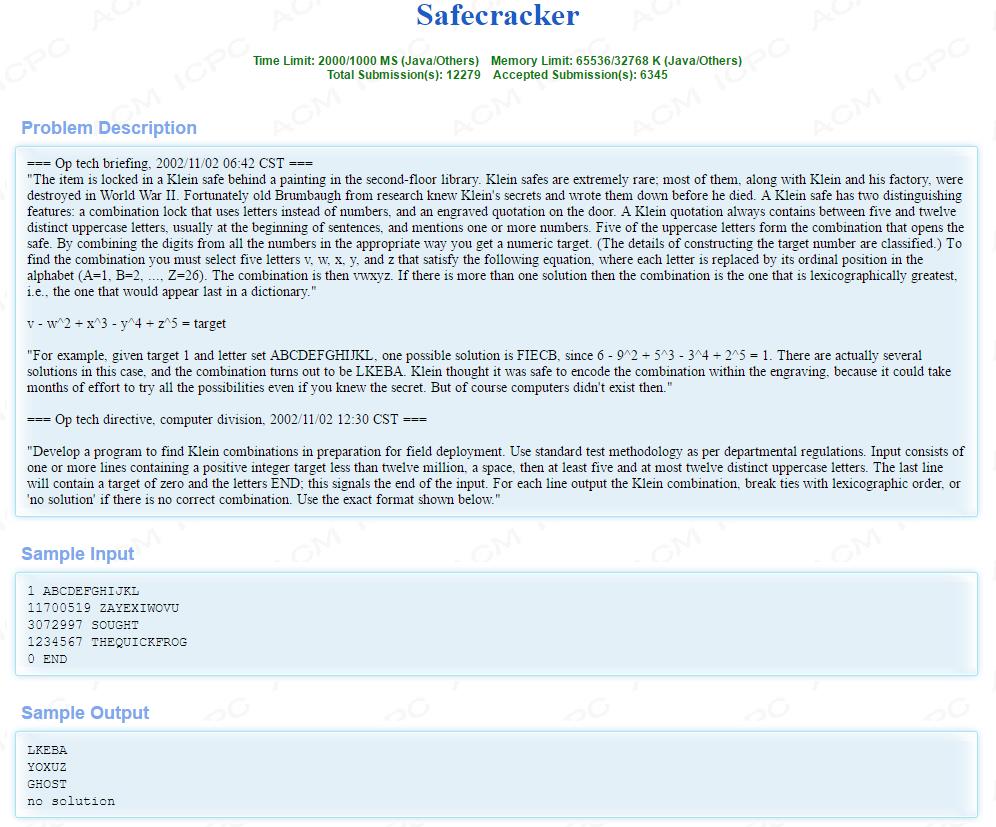
这个题目的题意:(自己结合百度翻译,简单的翻译了一下)
“这个项目是在一个在二楼图书馆一幅画的背后的克莱因的保险箱里。克莱因的保险柜是极为罕见的;他们中的大多数都随着克莱因和他的工厂在二战中被摧毁。幸运的是,老布伦博在他死之前研究发现了克莱因的秘密并写下来了。一个克莱因保险箱有两个特点是:一个使用字母而不是数字的组合锁,和一个刻在门上的引用。克莱因的引用总是包含五个和十二个不同的大写字母之间,通常在句首,并提到了一个或多个数字。五种大写字母的形成了打开保险柜的密码。通过把所有的数字与适当的方式相结合,你将得到一个数字目标。(构造目标密码的细节)要找到组合,你必须选择五个字母,v, w, x, y, 和 z 并满足下面的方程,其中每一个字母被替换的顺序位置在字母组中(a= 1,b= 2,…,z= 26)。组合是vwxyz。如果有一个以上的解决方案则选择字典最大的组合,即,组合会出现在字典上的最后一个。”
v - w^2 + x^3 - y^4 + z^5 = target
例如,给定的目标1和字母abcdefghijkl,一个可能的解决方案是fiecb,6 - 9 ^ 2 + 5 ^ 3 - 3 ^ 4 + 2 ^ 5 = 1。其实在这种情况下的几种解决方案,但最终组合是lkeba。克莱因认为雕刻的编码组合是安全的,因为它可能需要几个月的努力,尝试所有的可能性,即使你知道这个秘密。当然,电脑那时不存在了。”
“开发一个程序,以寻找克莱因组合,以准备现场部署。按部门规定使用标准测试方法。输入包含一个或多个包含一个正整数目标低于一千二百万,并且至少五个最多十二个不同的大写字母。最后一行将包含一个零和字母的组合码 END 意味着输入结束。每行输出的克莱因组合是乱序的,如果没有正确的组合输出\'no solution\'。使用下面显示的精确格式。”
简单的题意是:
从输入的字符串中,找出五个字母代替v、w、x、y、z,符合v - w^2 + x^3 - y^4 + z^5 = target 的所有答案中,输出最大的字符串。
我是思路是:获取长度为5的组合数,进行全排列并判断是否符合目标函数。
因为做这道题,我把全组合和全排列算法实现了一遍。http://www.cnblogs.com/xiezie/p/5574516.html
注意:我偷了个懒,这道题我下面的代码可以优化,不过思路一样。
可以不将结果存储起来,只需要实现字典序全排列,输出最后一个结果即可(将结果保存起来用字符串保存起来,一旦遇到下一个合适的字符串则替换)
以下是java实现:
import java.util.*; import java.io.*; public class Main1015{ public static void main(String[] arg){ Scanner scan = new Scanner(new BufferedInputStream(System.in)); int target; String inputStr; ArrayList<String> answers = new ArrayList<>(); ArrayList<String> combinations = new ArrayList<>(); ArrayList<Character> com = new ArrayList<>(5); while(true){ target = scan.nextInt(); inputStr = scan.next(); if(target ==0 && inputStr.contentEquals("END")){ break; } answers.clear(); combinations.clear(); com.clear(); //获取所有的组合 getCombinations(combinations,inputStr.toCharArray(),0,5,com); //获取全排列 for(int i = 0 ; i != combinations.size() ; i ++ ){ ArrayList<String> permutations = new ArrayList<>(); getAllPermutations(permutations,combinations.get(i).toCharArray(),0,combinations.get(i).length()); //判断是否符合target函数,符合则放入answer for(int j = 0 ; j != permutations.size() ; j ++){ if(target(permutations.get(j), target)){ answers.add(permutations.get(j)); } } } String answerCode = "" ; for(int i = 0 ; i != answers.size() ; i ++ ){ if(answers.get(i).compareTo(answerCode)>=1){ answerCode = answers.get(i); } } if(answerCode.equals("")){ System.out.println("no solution"); }else{ System.out.println(answerCode); } } scan.close(); } static boolean target(String s,int target){ char[] cs = s.toCharArray(); return (cs[0]-\'A\'+1)-Math.pow(cs[1]-\'A\'+1,2)+Math.pow(cs[2]-\'A\'+1,3)-Math.pow(cs[3]-\'A\'+1,4)+Math.pow(cs[4]-\'A\'+1,5)==target; } static void getAllPermutations(ArrayList<String> answers,char[] cs,int start,int len){ if(start == len ){ answers.add(String.valueOf(cs)); return; } for(int i = start ; i != len ; i ++){ swap(cs,i,start); getAllPermutations(answers,cs,start+1,len); swap(cs,i,start); } } static void getCombinations(ArrayList<String> list ,char[] cs, int start,int len,ArrayList<Character> com){//len为组合的长度 if(len == 0){ String s = ""; for(int i = 0 ; i != com.size() ; i ++){ s = s.concat(com.get(i).toString()); } list.add(s); return; } if(start==cs.length){ return; } com.add(cs[start]); getCombinations(list,cs,start+1,len-1,com); com.remove(com.size()-1); getCombinations(list,cs,start+1,len,com); } static void swap(char[] cs , int i , int j){ char t; t = cs[i]; cs[i] = cs[j]; cs[j] = t; } }
以上是关于HDOJ-ACM1015(JAVA) 运用 组合全排列实现的主要内容,如果未能解决你的问题,请参考以下文章