poj2046
Posted 神犇(shenben)
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了poj2046相关的知识,希望对你有一定的参考价值。
Gap
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 1829 | Accepted: 829 |
Description
Let‘s play a card game called Gap.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.
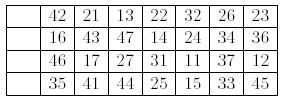
Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.
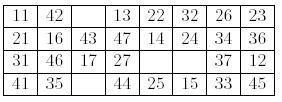
At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.
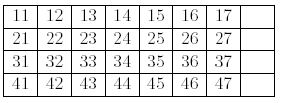
Your task is to find the minimum number of moves to reach the goal layout.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.

Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.

At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.

Your task is to find the minimum number of moves to reach the goal layout.
Input
The input starts with a line containing the number of initial layouts that follow.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Output
For each initial layout, produce a line with the minimum number of moves to reach the goal layout. Note that this number should not include the initial four moves of the cards of value 1. If there is no move sequence from the initial layout to the goal layout, produce "-1".
Sample Input
4 12 13 14 15 16 17 21 22 23 24 25 26 27 31 32 33 34 35 36 37 41 42 43 44 45 46 47 11 26 31 13 44 21 24 42 17 45 23 25 41 36 11 46 34 14 12 37 32 47 16 43 27 35 22 33 15 17 12 16 13 15 14 11 27 22 26 23 25 24 21 37 32 36 33 35 34 31 47 42 46 43 45 44 41 27 14 22 35 32 46 33 13 17 36 24 44 21 15 43 16 45 47 23 11 26 25 37 41 34 42 12 31
Sample Output
0 33 60 -1
Source
Japan 2003,Aizu
题意:如题目中图片2所示,每次从表中选择一个数字填入四个空格中的其中一个(能填入该空格的条件是即将填入该空格的数字=该空格左边的数+1)。
问最少需要几次操作,达到图片3的状态
问最少需要几次操作,达到图片3的状态
代码:
#include<cstdio> #include<cstring> using namespace std; const int M=1000007; struct data { char s[32],e[4],p[48]; int ans; }w[500000]; int id[M],ans; inline int BKDRHash(char *str) { int hash=0,q=0; while(++q<33)hash=hash*7+(*str++); return((hash&0x7FFFFFFF)%M); } inline void insert(char *c,int i) { int x=BKDRHash(c); while(id[x]>=0) { x+=7; if(x>=M)x%=M; } id[x]=i; } inline bool cmp(char *p,char *q) { for(int i=0;i<32;++i,++p,++q) if(*p!=*q)return 1; return 0; } inline int find(char *c) { int x=BKDRHash(c); while(id[x]>=0&&cmp(c,w[id[x]].s)) { x+=7; if(x>=M)x%=M; } return id[x]; } inline void get(char &a) { char ch=getchar(); while (ch<‘0‘||ch>‘9‘)ch=getchar(); for(a=0;ch>=‘0‘&&ch<=‘9‘;ch=getchar())a=a*10+ch-48; if((a==11)||(a==21)||(a==31)||(a==41))a=0; } inline void cpy(char *p,char *q,int n) { for(int i=0;i<n;++i,++p,++q)*p=*q; } inline int bfs() { int l=0,r=1,rr=2,i,k,s,p,e; do { cpy(w[rr].s,w[++l].s,32); for(i=0;i<4;++i) if(w[l].s[(e=w[l].e[i])-1]%10<7&&w[l].s[e-1]>0) { w[rr].s[e]=s=w[l].s[e-1]+1,w[rr].s[p=w[l].p[s]]=0; if((k=find(w[rr].s))<0) { ++r,++rr,cpy(w[r].e,w[l].e,4),cpy(w[r].p,w[l].p,48); w[r].e[i]=p,w[r].p[s]=e,w[r].ans=w[l].ans+1; insert(w[r].s,r); cpy(w[rr].s,w[l].s,32); } else w[rr].s[p]=s,w[rr].s[e]=0; if(!k)return w[l].ans+1; } }while(l<r); return -1; } int main() { int n,i,j,k; for(i=0;i<25;i+=8) for(j=0;j<7;++j)w[0].s[i+j]=(i/8+1)*10+j+1; scanf("%d",&n); while(n--) { memset(id,-1,sizeof(id)); insert(w[0].s,0); for(i=0;i<25;i+=8) for(w[1].s[i]=(i/8+1)*10+1,j=1;j<8;++j)get(w[1].s[i+j]),w[1].p[w[1].s[i+j]]=i+j; if(!find(w[1].s))printf("0\n"); else { for(k=i=0;i<25;i+=8) for(j=0;j<8;++j) if(!w[1].s[i+j])w[1].e[k++]=i+j; w[1].ans=0; insert(w[1].s,1); printf("%d\n",bfs()); } } return 0; }
以上是关于poj2046的主要内容,如果未能解决你的问题,请参考以下文章