POJ 2986 A Triangle and a Circle

Posted 2020-07-24 GFY

题意:给定一个三角形，以及一个圆的圆心坐标和半径，求圆和三角形的相交面积。

思路：

用三角剖分，三角形上每个线段都变成这个线段与圆心的三角形，然后算出每个三角形与圆的相交面积，然后根据有向面积的正负累加到答案中即可。

分为5种情况:

(1)两个点到圆心距离都小于R

 

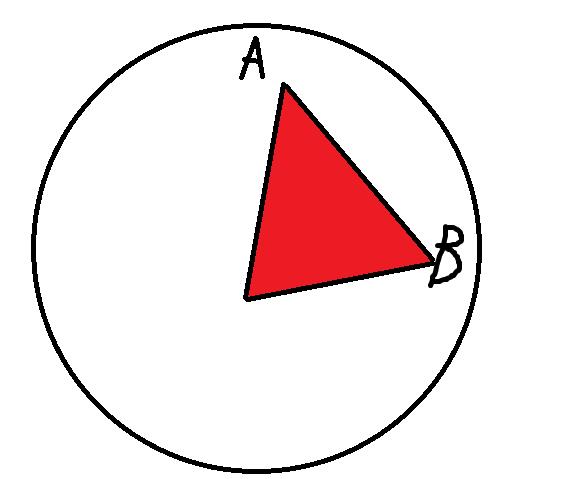
此时只要计算三角形的有向面积即可。

(2)两个点距离都大于R，且两点连线距离大于R

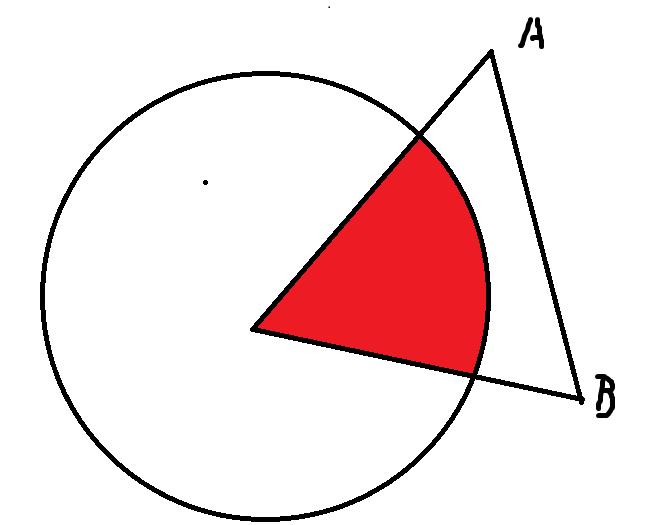
此时只需要计算这个扇形面积即可

(3)两点到圆心距离都大于R，但两点连线到圆心距离小于R，且这两点所在角有一个钝角。

 

 

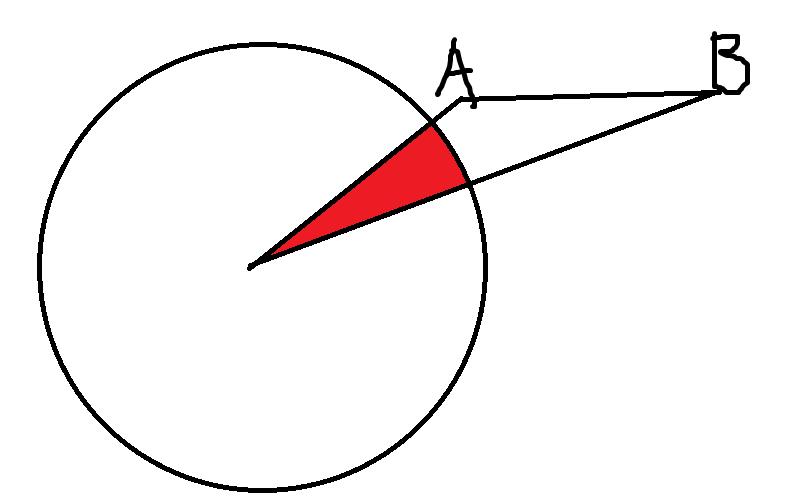
此时也是计算扇形面积

(4)两点到圆心距离都大于R，两点连线到圆心距离小于R,且两点所在角都是锐角。

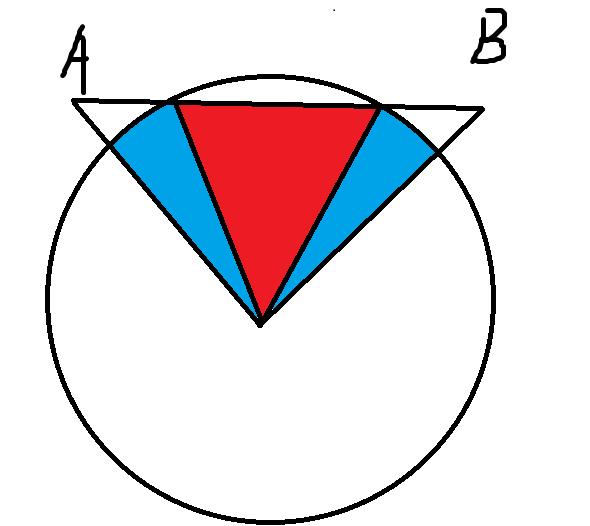
此时需要计算中间三角形有向面积，以及蓝色部分扇形有向面积.

(5)只有一点到圆心距离大于R

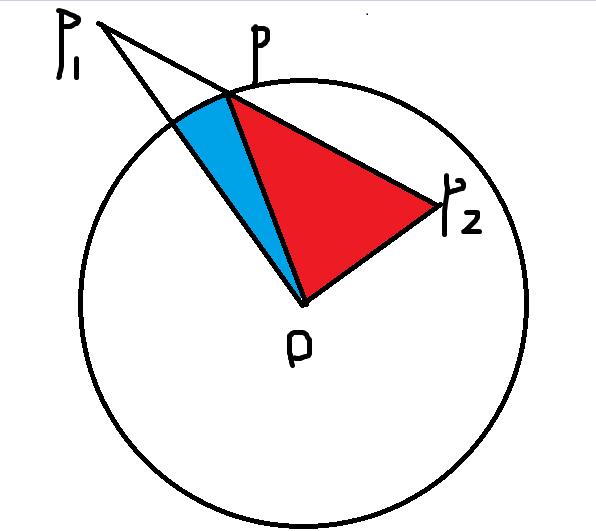
此时只需要其中一个三角形有向面积，和另一个扇形的有向面积.

代码:

  1 #include<algorithm>
  2 #include<cstdio>
  3 #include<cmath>
  4 #include<cstring>
  5 #include<iostream>
  6 struct Point{
  7     double x,y;
  8     Point(){}
  9     Point(double x0,double y0):x(x0),y(y0){}
 10 }p[200005],a[5],O;
 11 struct Line{
 12     Point s,e;
 13     Line(){}
 14     Line(Point s0,Point e0):s(s0),e(e0){}
 15 };
 16 int n;
 17 double R;
 18 const double eps=1e-8;
 19 const double Pi=acos(-1);
 20 double sgn(double x){
 21     if (x>eps) return 1.0;
 22     if (x<-eps) return -1.0;
 23     return 0;
 24 }
 25 Point operator *(Point p1,double x){
 26     return Point(p1.x*x,p1.y*x);
 27 }
 28 Point operator /(Point p1,double x){
 29     return Point(p1.x/x,p1.y/x);
 30 }
 31 double operator /(Point p1,Point p2){
 32     return p1.x*p2.x+p1.y*p2.y;
 33 }
 34 double operator *(Point p1,Point p2){
 35     return p1.x*p2.y-p1.y*p2.x;
 36 }
 37 Point operator +(Point p1,Point p2){
 38     return Point(p1.x+p2.x,p1.y+p2.y);
 39 }
 40 Point operator -(Point p1,Point p2){
 41     return Point(p1.x-p2.x,p1.y-p2.y);
 42 }
 43 double dis(Point p1){
 44     return sqrt(p1.x*p1.x+p1.y*p1.y);
 45 }
 46 double dis(Point p1,Point p2){
 47     return dis(Point(p1.x-p2.x,p1.y-p2.y));
 48 }
 49 double sqr(double x){
 50     return x*x;
 51 }
 52 double dist_line(Line p){
 53     double A,B,C,dist;
 54     A=p.s.y-p.e.y;
 55     B=p.s.x-p.e.x;
 56     C=p.s.x*p.e.y-p.s.y*p.e.x;
 57     dist=fabs(C)/sqrt(sqr(A)+sqr(B));
 58     return dist;
 59 }
 60 double get_cos(double a,double b,double c){
 61     return (b*b+c*c-a*a)/(2*b*c);
 62 }
 63 double get_angle(Point p1,Point p2){
 64     if (!sgn(dis(p1))||!sgn(dis(p2))) return 0.0;
 65     double A,B,C;
 66     A=dis(p1);
 67     B=dis(p2);
 68     C=dis(p1,p2);
 69     if (C<=eps) return 0.0;
 70     return acos(get_cos(C,A,B));
 71 }
 72 Point get_point(Point p){
 73     double T=sqr(p.x)+sqr(p.y);
 74     return Point(sgn(p.x)*sqrt(sqr(p.x)/T),sgn(p.y)*sqrt(sqr(p.y)/T));
 75 }
 76 double S(Point p1,Point p2,Point p3){
 77     return fabs((p2-p1)*(p3-p1))/2;
 78 }
 79 double work(Point p1,Point p2){
 80     double f=sgn(p1*p2),res=0;
 81     if (!sgn(f)||!sgn(dis(p1))||!sgn(dis(p2))) return 0.0;
 82     double l=dist_line(Line(p1,p2));
 83     double a=dis(p1);
 84     double b=dis(p2);
 85     double c=dis(p1,p2);
 86     if (a<=R&&b<=R){
 87         return fabs(p1*p2)/2.0*f;
 88     }
 89     if (a>=R&&b>=R&&l>=R){
 90         double ang=get_angle(p1,p2);
 91         return fabs((ang/(2.0))*(R*R))*f;
 92     }
 93     if (a>=R&&b>=R&&l<=R&&(get_cos(a,b,c)<=0||get_cos(b,a,c)<=0)){
 94         double ang=get_angle(p1,p2);
 95         return fabs((ang/(2.0))*(R*R))*f;
 96     }
 97     if (a>=R&&b>=R&&l<=R&&(get_cos(a,b,c)>0&&get_cos(b,a,c)>0)){
 98         double dist=dist_line(Line(p1,p2));
 99         double len=sqrt(sqr(R)-sqr(dist))*2.0;
100         double ang1=get_angle(p1,p2);
101         double cos2=get_cos(len,R,R);
102         res+=fabs(len*dist/2.0);
103         double ang2=ang1-acos(cos2);
104         res+=fabs((ang2/(2))*(R*R));
105         return res*f;
106     }
107     if ((a>=R&&b<R)||(a<R&&b>=R)){
108         if (b>a) std::swap(a,b),std::swap(p1,p2);
109         double T=sqr(p1.x-p2.x)+sqr(p1.y-p2.y);
110         Point u=Point(sgn(p1.x-p2.x)*sqrt(sqr(p1.x-p2.x)/T),sgn(p1.y-p2.y)*sqrt(sqr(p1.y-p2.y)/T));
111         double dist=dist_line(Line(p1,p2));
112         double len=sqrt(R*R-dist*dist);
113         double len2=sqrt(sqr(dis(p2))-sqr(dist));
114         if (fabs(dis(p2+u*len2)-dist)<=eps) len+=len2;
115         else len-=len2;
116         Point p=p2+u*len;
117         res+=S(O,p2,p);
118         double ang=get_angle(p1,p);
119         res+=fabs((ang/2.0)*R*R);
120         return res*f;
121     }
122     return 0;
123 }
124 int main(){
125     O=Point(0,0);
126     while (scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf",&p[1].x,&p[1].y,&p[2].x,&p[2].y,&p[3].x,&p[3].y,&O.x,&O.y,&R)!=EOF){
127         n=3;
128         p[n+1]=p[1];
129         for (int i=1;i<=4;i++)
130          p[i].x-=O.x,p[i].y-=O.y;
131         O.x=0;O.y=0; 
132         double ans=0;
133         for (int i=1;i<=n;i++)
134          ans+=work(p[i],p[i+1]);
135         ans=fabs(ans);  
136         printf("%.2f\\n",ans); 
137     }
138 }