数据结构一栈和队列

Posted 2020-07-24 My_Blog_Days

1、两个栈实现一个队列，实现在队列尾部插入节点，在队列头部删除节点。

        若为入队列则进stack1，若要出队列可分2种情况：a、若stack2为空，根据栈先进后出的特性应该先将stack1的元素pop出，进stack2。b、若 stack2不为空，可以说明stack2是前几次操作由stack1出栈的元素，符合队列先进先出的原则，则出队列操作可以直接使stack2中的栈顶元素出栈就可以了。如下图：

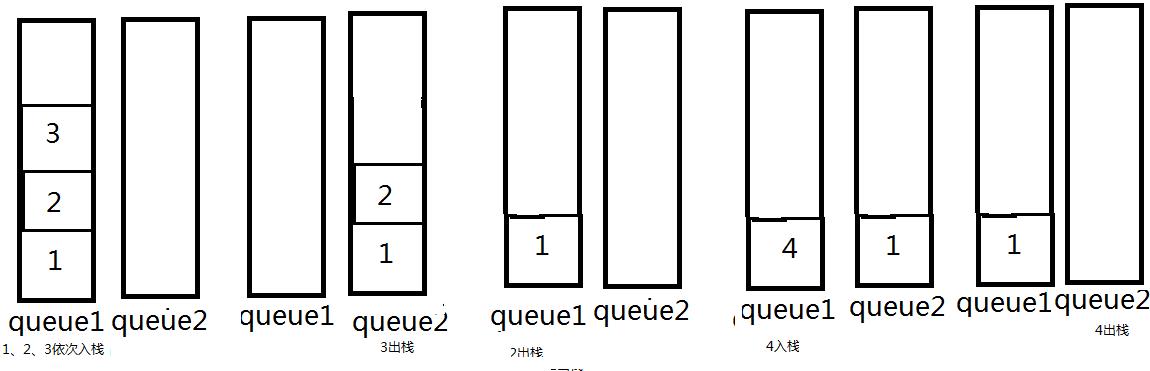
若有3个元素1,2,3依次入队列:

第一种情况：stack1和stack2都为空，入队列为进stack1，若要出队列，则将stack1中的元素依次出栈，push到 stack2 中，pop出stack2的栈顶元素则  为出队列.

第二种情况：此时stack2不为空若元素4要入队列则进stack1，若要出队列，此时stack2不为空则可以直接pop出栈顶元素2即可

 

 代码如下：

#include<stack>
template<class T>
class Queue
{public:
    Queue()
    {}
    ~Queue()
    {}
    void PushTail(const T&x)
    {
        stack1.push(x);
    }
    void PopHead()
    {
        if (stack2.size()<=0)
        {
            while (stack1.size() > 0)
            {
                T &a = stack1.top();
                stack1.pop();
                stack2.push(a);
            }
        }
        if (stack2.size() == 0)
            return;
        stack2.pop();
    }
private:
    stack<T> stack1;
    stack<T> stack2;

};

2、两个队列实现一个栈

代码如下：

#include<queue>
template<class T>
class Stack
{
public:
    Stack()
    {}
    ~Stack()
    {}
    void PushHead(const T&x)
    {
        queue1.push(x);
    }
    void PopTail()
    {
        assert(queue1.size()>0 || queue2.size()>0)
        if (queue2.size() <= 0)
        {
            while (queue.size() > 0)
            {
                T &a = queue1.front();
                queue1.pop();
                queue2.push(a);
            }
            queue2.pop();
        }
        if (queue1.size() <= 0)
        {
            while (queue2.size() > 0)
            {
                T &a = queue2.front();
                queue2.pop();
                queue1.push(a);
            }

            queue1.pop();

            }
        } 

private:
 queue<T> queue1;
 queue<T> queue2; 
};

3、定义栈的数据结构，实现一个可以找到栈的最小元素的min函数，调用min、pop、push的时间复杂度为O(1);

分析：若每次新元素入栈时，排序让最小的元素在栈顶，这样可以实现min函数的时间复杂度为O(1)，但一旦换了位置就不能满足栈先进后出的特点。

         若在栈中设置一个变量，存放当前栈中最小元素，但是一旦最小元素pop出后则无法得到现在的最小元素。

         可以设置一个辅助栈，每次数据入栈时，进入辅助栈的元素可以设置成（新入栈元素与以前入栈元素的最小值中的较小值）

代码如下：其中MinDate为存放数据的栈，Min为辅助栈

#include<stack>
template<class T>
class MinOfStack

{

public：

   void push(const T&x)

    {
      if (Min.size() == 0 || x < Min.top())
     {
          Min.push(x)
     }
     else Min.push(Min.top());

  }
  void pop(const T&x)
  {
     assert(Min.size()>0 && MinData.size() > 0)
     MinData.pop();
     Min.pop();
  }

 T& min()const
{
   assert(Min.size() > 0 && MinData.size() > 0)
   return Min.pop();
}
private:
   stack<T> Min;
   stack<T> MinData;
};

 4、输入两个序列第一个表示栈的压入顺序，判断第二个序列是否为该该栈的弹出顺序。

分析:若下一个要弹出的刚好是栈顶元素则直接弹出，若要弹出的不是栈顶元素则将压栈序列中没有压入的数压入栈直到下一个需要弹出的元素压入栈顶，如果所有元素都压入栈还没有找到下一个要弹出的元素，那该序列不可能是一个弹出序列。

代码如下：

#include<stack>
bool IsPopOrder(const int*pPush, const int*pPop, int Length)
{
    //合法条件
    if (pPush != NULL&&pPop != NULL&&Length > 0)
    {
        const int*pNextPop = pPush;
        const int*pNextPush = pPush;
        stack<int> PopStack;
        while (pNextPop - pPop > Length)
        {
            while (PopStack.empty() || PopStack.top() != *pPop)
            {
                if (pNextPush - pPush == Length)//输入序列走完
                    break;
                PopStack.push(*pNextPush);
                pNextPush++;
            }
            if (PopStack.top() != *pPop)
                break;
            pNextPop++;//PopStack.top()== *pPop
        }
        if (pNextPop - pPop == Length&&PopStack.empty())
            return true;
    }
    return false;
}