hdu 3870 最小割转化为最短路径2

Posted 2020-07-24 iEdson

Catch the Theves

Problem Description

A group of thieves is approaching a museum in the country of zjsxzy,now they are in city A,and the museum is in city B,where keeps many broken legs of zjsxzy.Luckily,GW learned the conspiracy when he is watching stars and told it to zjsxzy.
Zjsxzy decided to caught these thieves,and he let the police to do this,the police try to catch them on their way from A to B. Although the thieves might travel this way by more than one group, zjsxzy\'s excellent police has already gather the statistics that the cost needed on each road to guard it. 
Now ,zjsxzy\'s conutry can be described as a N*N matrix A,Aij indicates the city(i,j) have bidirectionals road to city(i+1,j) and city(i,j+1),gurad anyone of them costs Aij.
Now give you the map,help zjsxzy to calculate the minimium cost.We assume thieves may travel in any way,and we will catch all passing thieves on a road if we guard it.

 

 

Input

The first line is an integer T,followed by T test cases.
In each test case,the first line contains a number N(1<N<=400).
The following N lines,each line is N numbers,the jth number of the ith line is Aij.
The city A is always located on (1,1) and the city B is always located on (n,n).
Of course,the city (i,j) at the last row or last line won\'t have road to (i,j+1) or (i+1,j).

 

 

Output

For each case,print a line with a number indicating the minimium cost to arrest all thieves.

 

 

Sample Input

1

3

10 5 5

6 6 20

4 7 9

 

 

Sample Output

18

 

hint 

The map is like this:

---

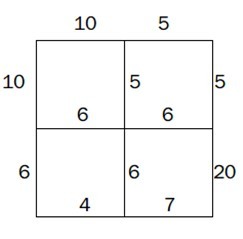
思路:和上一题http://www.cnblogs.com/EdsonLin/p/5574033.html差不多，不过这一题直接给了点权，所以逻辑上感觉好理解一点吧

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#include <vector>
#include <algorithm>
#include <ctime>
using namespace std;

//#define EdsonLin

#ifdef EdsonLin
#define debug(...) fprintf(stderr,__VA_ARGS__)
#else
#define debug(...)
#endif //EdsonLin

typedef long long ll;
typedef double db;
const int inf = 0x3f3f3f;
const int MAXN = 410;
const int MAXNN = 160000;
const int MAXM = 1e6;
//const int MAXM = 3e4+100;
const int MOD = 1000000007;
const db eps = 1e-3;
#define PB push_back

struct dij{
    int n,m;
    int first[MAXNN];
    struct edge{
        int st,to,next,dist;
    };
    vector<edge>e;
    int top;
    int d[MAXNN]; //s到各节点的距离
    int done[MAXNN]; //是否已经被永久标记
    int p[MAXNN]; //记录上一条边
    struct heapnode{
        int st;
        int dist;
        bool operator < (const heapnode& rhs) const {
            return dist>rhs.dist;
        }
    };
    void init(int n){
        this->n = n;
        memset(first,-1,sizeof(first));
        top = 0;
        e.clear();
    }
    void addedge(int u,int v,int dist){
        /*e[top].st = u;
        e[top].to = v;
        e[top].dist = dist;
        e[top].next = first[u];
        first[u] = top++;*/
        edge a;
        a.st = u;
        a.to = v;
        a.dist = dist;
        a.next  = first[u];
        e.PB(a);
        first[u] = top++;
        //cout<<first[u]<<endl;
        //cout<<top<<endl;
    }

    void pqdij(int s){
        priority_queue<heapnode>Q;
        heapnode a;
        for(int i=0;i<n;i++)
            d[i] = inf;
        d[s] = 0;
        memset(done,0,sizeof(done));
        a.dist = 0;
        a.st = s;
        Q.push(a);
        while(!Q.empty()){
            heapnode x = Q.top();
            Q.pop();
            int u = x.st;
            if(done[u])continue;
            done[u] = 1;
            for(int i=first[u];i!=-1;i=e[i].next){
                if(d[e[i].to]>d[u]+e[i].dist){
                    d[e[i].to] = d[u] + e[i].dist;
                    p[e[i].to] = i;
                    a.dist = d[e[i].to];
                    a.st = e[i].to;
                    Q.push(a);
                }
            }
        }
    }
}solver;


int readint(){int x;scanf("%d",&x);return x;}

int main()
{
    #ifdef EdsonLin
        //freopen("1.in","r",stdin);
        //freopen("1.out","w",stdout);
        int _time_ed = clock();
    #endif //EdsonLin

    int T;
    scanf("%d",&T);
    int mc=0,grid[MAXN][MAXN];
    while(mc++<T){
        int n,st,ed;
        cin>>n;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++)
                grid[i][j] = readint();
        }
        st = 0;ed = (n-1)*(n-1)+1;
        solver.init(ed+1);
        for(int i=1;i<n;i++){
            for(int j=1;j<n;j++){
                int cur = (i-1)*(n-1)+j;
                if(i==1){
                    solver.addedge(cur,ed,grid[i][j]);
                    solver.addedge(ed,cur,grid[i][j]);
                }
                if(i!=n-1){
                    solver.addedge(cur,cur+n-1,grid[i+1][j]);
                    solver.addedge(cur+n-1,cur,grid[i+1][j]);
                }
                if(i==n-1){
                    solver.addedge(st,cur,grid[i+1][j]);
                    solver.addedge(cur,st,grid[i+1][j]);
                }
                if(j==1){
                    solver.addedge(st,cur,grid[i][j]);
                    solver.addedge(cur,st,grid[i][j]);
                }
                if(j!=n-1){
                    solver.addedge(cur,cur+1,grid[i][j+1]);
                    solver.addedge(cur+1,cur,grid[i][j+1]);
                }
                if(j==n-1){
                    solver.addedge(cur,ed,grid[i][j+1]);
                    solver.addedge(ed,cur,grid[i][j+1]);
                }
            }
        }
        solver.pqdij(st);
        printf("%d\\n",solver.d[ed]);
    }

    #ifdef EdsonLin
        debug("time: %d\\n",int(clock()-_time_ed));
    #endif //EdsonLin
   // cout << "Hello world!" << endl;
    return 0;
}

View Code