算法练习：最小生成树 (Minimum Spanning Tree)

Posted 2020-07-22

（注：此贴是为了回答同事提出的一个问题而匆匆写就，算法代码只求得出答案为目的，效率方面还有很大的改进空间）

 

最小生成树是指对于给定的带权无向图，需要生成一个总权重最小的连通图。
其问题描述及算法可以详见：https://en.wikipedia.org/wiki/Minimum_spanning_tree
以下我选用其中一个简单的算法描述，编写 Python 代码尝试解决此问题。

下面是同事提出的问题的原图：

 

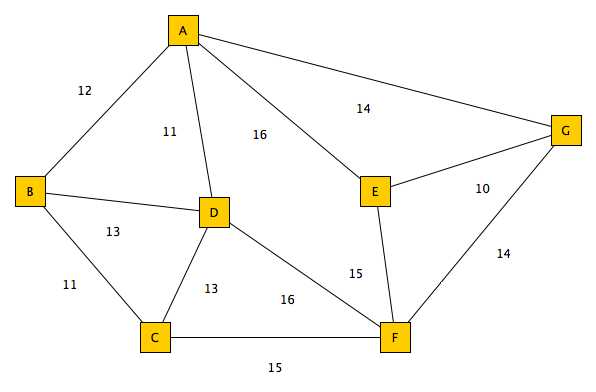
程序：

 1 # coding: utf-8
 2 
 3 from sets import Set
 4 
 5 def edge_name(v1, v2):
 6     if v1 < v2:
 7         return v1 + v2
 8     return v2 + v1
 9 
10 
11 # Prim algorithm
12 def mst(vectors, costs, vectors_in_g, edges_in_g):
13     if len(vectors) == len(vectors_in_g):
14         return (vectors_in_g, edges_in_g)
15 
16     min_cost = max(costs.values()) + 1
17     remaining_vectors = vectors.difference(vectors_in_g)
18     next_vector = ‘‘
19     next_edge = ‘‘
20 
21     for x in vectors_in_g:
22         for y in remaining_vectors:
23             ename = edge_name(x, y)
24             if ename not in costs:
25                 continue
26             cost = costs[ename]
27             if cost < min_cost:
28                 next_vector = y
29                 next_edge = ename
30                 min_cost = cost
31 
32     if next_vector <> ‘‘ and next_edge <> ‘‘:
33         new_vectors_in_g = vectors_in_g.copy()
34         new_edges_in_g = edges_in_g[:]
35         new_vectors_in_g.add(next_vector)
36         new_edges_in_g.append(next_edge)
37 
38         return mst(vectors, costs, new_vectors_in_g, new_edges_in_g)
39     else:
40         raise Exception("The MST can not be found.")
41 
42 my_vectors = Set([‘a‘, ‘b‘, ‘c‘, ‘d‘, ‘e‘, ‘f‘, ‘g‘])
43 my_costs = {
44     ‘ab‘: 12,
45     ‘ad‘: 11,
46     ‘ae‘: 16,
47     ‘ag‘: 14,
48     ‘bc‘: 11,
49     ‘bd‘: 13,
50     ‘cd‘: 13,
51     ‘cf‘: 15,
52     ‘df‘: 16,
53     ‘ef‘: 15,
54     ‘eg‘: 10,
55     ‘fg‘: 14
56 }
57 
58 vs, es = mst(my_vectors, my_costs, Set(list(my_vectors)[0]), [])
59 
60 print vs
61 print es
62 
63 total_cost = 0
64 for e in es:
65     total_cost += my_costs[e]
66 
67 print total_cost

 

程序输出如下：

Set([‘a‘, ‘c‘, ‘b‘, ‘e‘, ‘d‘, ‘g‘, ‘f‘])
[‘ad‘, ‘ab‘, ‘bc‘, ‘ag‘, ‘eg‘, ‘fg‘]
72

 

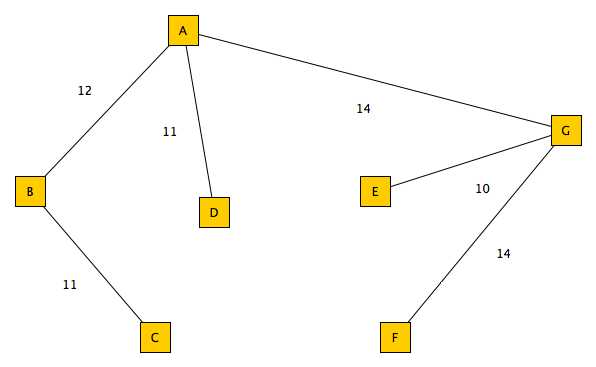
从输出结果可知最优解的总权重72. 图示如下：