一个小demo的开发日记
Posted Betairy linkzeldagg
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一个小demo的开发日记相关的知识,希望对你有一定的参考价值。
时间倒退回2016年4月10日,这个工程刚开始的时候 ——
就不说做这个的原因和为什么要做个这个了。嗯…感觉好蠢。
一上来什么都没有。我决定把注意力先放到重点 —— 场景最中间那棵树上面。
在这个时候,我手里有一份Ogre(另一个游戏引擎,开源,无GUI)上的分形树。至于分形树是个啥,就先当成一个可以画出三维的树的程序好了。
然而我觉得用Unity能让我更快的完成这个东西,毕竟时间紧迫,离deadline只剩12天了。而现在我手上什么都没有,而且对Unity一无所知,简直…太糟了w
所以第一件事是把之前Ogre上的demo移植到Unity上来,并尝试改进一下。原来Ogre里的那份demo的效果实在是不敢恭维,尤其是加上树叶之后简直没法看。
上几张图你们感受一下:


(我要澄清一下我这个坑还在填!没有坑!虽然感觉没人会在意这个hh)
总之根本没法看,树叶很丑,整个树枝的结构也比较生硬。
但是先不管,先把这个东西移植到Unity上来吧?然后再改。毕竟当时我觉得这种方法是可以画出来像样的树(包括树叶)的,后来事实也证明确实如此。
好,先停一下。
上图中的树是怎么画出来的?
上一期里说过,3D模型是由顶点构成的面来描述的,市面上常见的建模软件(3dmax, maya…)最后保存出的文件里就包含有这些顶点的信息;但我们同样也可以不依靠于模型文件,自己通过代码来生成这些顶点信息。
但就算如此,首先,我们需要用程序来描述出一棵树的形状,有着丰富的细节,有着美观的轮廓,有着…
一个个往里输顶点坐标乱七八糟的不是要疯掉。
但好在1967年,Mandelbrot在《科学》杂志上发表了分形理论。
它所描述的是一种结构 —— 不一定是形状 —— 这种结构的局部特征和整体特征相似,以一种"迭代"的方式去产生细节(虽然这么说并不好),这使得这种结构具有着无穷精细的结构…

来举个例子。
比如我定义一种方法:
一根还没有分过叉的线段会在顶端分出左右45度的两条新线段。
或许在最开始是这样的(图中线比较短):

使用一次上述的规则:

再来一次:

…:



是不是有点像一棵树了?
同时,这种结构非常方便用程序(数学)语言来描述。我只需要知道一条线段怎么画,然后我有这个结构,我就可以用这个结构里每条线段的位置、长度、角度等信息来画不同的许许多多的线段出来,它们组成一个完整图形。
说白了,我们只需要确定一个线段的"顶点"位置,然后把这些位置复制好多份,每份都做不同的旋转缩放平移,再一起组成一个大数组;同时这种旋转缩放平移可以用递归的方法完成。
看起来工作量是不是小了很多。
不过,慢着。平移,缩放还好说;
我们真的知道要如何计算三维空间中点A绕轴B旋转C度产生的点D的坐标吗?
…不知道。所以我们没法继续。(就算知道也请当做不知道ww)
好,毫无头绪。那来把情况简化一下,看看二维空间中的情况。
二维空间中旋转轴只能垂直于"纸面"。
再简化一下,这个轴过原点。
(不过原点的可以视为平移和绕过原点的轴旋转两个操作的组合。)
来试着描述一下这个点,比如…(1,0)好了(不要在意图有多丑Orz)
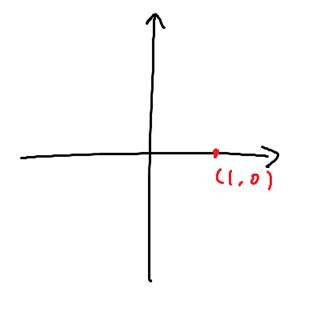
现在我们把它绕原点逆时针旋转90度,它变成了(0,1):

不好办。
不过二维平面中的旋转,高中的数学老师应该多少是会提一下的。
嗯对。就是复数。
来把这个平面想象成复平面,(1,0)就是1,(0,1)就是i。
复数相乘,幅角相加,模长相乘。所以想要把1+0i逆时针旋转90度,需要把它乘上幅角90度的复数0+1i。
我还想再转45度,,注意这里乘数模长一定为1:

看起来能行。
那么把情况放到三维空间中呢?
三维空间中的情形与二维平面中的复数十分相似。只不过这里不再是复数,而是一种被称为"四元数"的数,它的基本形式是这样:
用这样一个数和三维空间中的坐标相乘可以得到这个坐标绕某个轴旋转了某度后的坐标点。同时,它还可以连乘,Q1 * Q2表示一个先做了Q2再做Q1的旋转。
四元数Q中的x,y,z,w四个参量就代表了某种特定的旋转方式。
但有一点是需要注意的,四元数的乘法并不满足交换律,所以在计算上要多加注意。
事实上,四元数和旋转矩阵之间大概是等价的(望纠正ww),矩阵只是把四元数写开了而已。
那么我们如何根据我们想做的旋转得到x,y,z,w的值呢?这牵扯到一堆数学计算,没办法展开说,有兴趣可以去网上搜搜。然而Unity给我们提供了一系列方法来简化这些计算。
实际上,它们真的很方便。
Unity中代表四元数的类是Quaternion,它有许多成员函数,比如:
public static Quaternion AngleAxis(float angle, Vector3 axis)
这个函数产生一个可以描述"绕轴axis旋转angle度"的四元数。然后我们只需要将其和Vector3直接乘起来就行了。比如:
1 Quaternion q = Quaternion.AngleAxis(50.0f, new Vector3(0, 1, 0)); 2 Vector3 v = new Vector3(1, 1, 1); 3 Vector3 result = q * v;
现在,我们已经有了可以旋转的方法;
那如何在Unity中用代码生成顶点数组并让它成为一个模型呢?
Unity中有个组件叫做MeshFilter,更改它就可以改变gameObject的外观。
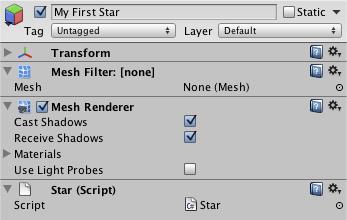
比如这样:
1 public void RenderMesh() 2 { 3 mFilter = gameObject.GetComponent<MeshFilter>(); 4 FractalRenderState state; 5 state.centerPos = new Vector3(0, 0, 0); 6 state.rotation = Quaternion.identity; 7 8 RenderNodeRec(state, startNode); 9 10 Debug.Log("Render summary: Vertices count = " + verticesCount + " Indices count = " + indicesCount + " (" + fractalType.ToString() + ")"); 11 12 Mesh mesh = new Mesh(); 13 mesh.hideFlags = HideFlags.DontSave; 14 mesh.vertices = vertices; 15 mesh.triangles = indices; 16 17 if (renderNormals) { mesh.normals = normals; } 18 if (renderUV1s) { /*mesh.uv = uv1s;*/ } 19 if (renderUV2s) { /*mesh.uv2 = uv2s;*/ } 20 if (renderTangents) { /*mesh.tangents = tangents*/ } 21 22 mFilter.mesh = mesh; 23 }
这里vertices和indices都是数组,它们存放了之前提到的顶点数组和顶点索引(顺序)。
如果在Start的时候调用RenderMesh,就可以更换模型。
Update的时候调用的话,可以任性的每帧都换一个模型。当然,会卡。
这里有个网上的更加直观的例子:
1 public void RenderMesh() 2 { 3 mFilter = gameObject.GetComponent<MeshFilter>(); 4 Mesh mesh = new Mesh(); 5 6 //顶点坐标 7 Vector3[] vertices = new Vector3[] 8 { 9 new Vector3( 1, 0, 1), 10 new Vector3( 1, 0, -1), 11 new Vector3(-1, 0, 1), 12 new Vector3(-1, 0, -1), 13 }; 14 15 //UV坐标 16 Vector2[] uv = new Vector2[] 17 { 18 new Vector2(1, 1), 19 new Vector2(1, 0), 20 new Vector2(0, 1), 21 new Vector2(0, 0), 22 }; 23 24 //三角形索引 25 int[] triangles = new int[] 26 { 27 0, 1, 2, 28 2, 1, 3, 29 }; 30 31 mesh.vertices = vertices; 32 mesh.uv = uv; 33 mesh.triangles = triangles; 34 35 mFilter.mesh = mesh; 36 }
UV坐标即纹理坐标。它创建了一个简单的有纹理的正方形,可以试着在纸上画一下。
Mesh还有其它的属性可以被设置,除了vertices, uv, triangles之类还有uv2,uv3,tangent等等。这样我们就可以用代码来创建一个3D物体了。
回到最开始的问题上来:我们要做的,是渲染一个构成树的最基本的元素,然后用无数个它进行位移、旋转等变换组成一棵树:
比如一根棍(长方体),就像之前图中的线段一样。
可以稍微对顶点位置啥的打打草稿,之后我们就可以把它封入一个函数中了。
在我的demo里这个函数的参数比较多。
1 public override void Express( 2 Vector3[] vertices, 3 ref int verticesCount, 4 int[] indices, 5 ref int indicesCount, 6 Vector3[] normals, 7 ref int normalsCount, 8 Vector2[] uvs, 9 ref int uvsCount, 10 Vector2[] uv2s, 11 ref int uv2sCount, 12 Vector4[] tangents, 13 ref int tangentsCount, 14 ref FractalRenderState state 15 ) 16 { 17 /* 18 z 19 y -+ 20 /|\\ /| Normals: +0 +8 +16 21 | (7)--------(6) (0) (-1, -1, -1) -Z -X -Y 22 | / | / / | (1) ( 1, -1, -1) -Z +X -Y 23 |/ / / | (2) ( 1, -1, 1) +X +Z -Y 24 (4)--+-----(5) | (3) (-1, -1, 1) +Z -X -Y 25 | (3) - - + -(2) (4) (-1, 1, -1) -Z -X +Y 26 | / | / (5) ( 1, 1, -1) -Z +X +Y 27 |/ | / (6) ( 1, 1, 1) +X +Z +Y 28 ----(0)--------(1)-----> x (7) (-1, 1, 1) +Z -X +Y 29 /| 30 / | 31 / | 32 33 0154 015 054 0 5 1 0 4 5 34 1265 126 165 9 6 2 9 13 6 35 2376 237 276 10 7 3 10 14 7 36 0473 047 073 8 15 12 8 11 15 37 4567 456 467 20 22 21 20 23 22 38 0321 032 021 16 18 19 16 17 18 39 */ 40 float lenth = 0.05f, width = 0.05f, height = 1.0f;//X, Z, Y 41 //float lenth = 0.05f * (Mathf.Log(growRate, 2.0f) - 4f), width = 0.05f * (Mathf.Log(growRate, 2.0f) - 4f), height = 1.0f;//X, Z, Y 42 43 #region Vertices 44 45 vertices[verticesCount + 0] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 46 vertices[verticesCount + 1] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 47 vertices[verticesCount + 2] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 48 vertices[verticesCount + 3] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 49 vertices[verticesCount + 4] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 50 vertices[verticesCount + 5] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 51 vertices[verticesCount + 6] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 52 vertices[verticesCount + 7] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 53 54 vertices[verticesCount + 0 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 55 vertices[verticesCount + 1 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 56 vertices[verticesCount + 2 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 57 vertices[verticesCount + 3 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 58 vertices[verticesCount + 4 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 59 vertices[verticesCount + 5 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 60 vertices[verticesCount + 6 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 61 vertices[verticesCount + 7 + 8] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 62 63 vertices[verticesCount + 0 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 64 vertices[verticesCount + 1 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, -width / 2.0f) * growRate) + centerPos); 65 vertices[verticesCount + 2 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 66 vertices[verticesCount + 3 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, 0, +width / 2.0f) * growRate) + centerPos); 67 vertices[verticesCount + 4 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 68 vertices[verticesCount + 5 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, -width / 2.0f) * growRate) + centerPos); 69 vertices[verticesCount + 6 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(+lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 70 vertices[verticesCount + 7 + 16] = state.centerPos + state.rotation * (rotation * (new Vector3(-lenth / 2.0f, height, +width / 2.0f) * growRate) + centerPos); 71 72 #endregion 73 74 #region Normals 75 //-Z 76 normals[normalsCount + 0] = state.rotation * rotation * Vector3.back; 77 normals[normalsCount + 1] = state.rotation * rotation * Vector3.back; 78 normals[normalsCount + 4] = state.rotation * rotation * Vector3.back; 79 normals[normalsCount + 5] = state.rotation * rotation * Vector3.back; 80 81 //+Z 82 normals[normalsCount + 10] = state.rotation * rotation * Vector3.forward; 83 normals[normalsCount + 3] = state.rotation * rotation * Vector3.forward; 84 normals[normalsCount + 7] = state.rotation * rotation * Vector3.forward; 85 normals[normalsCount + 14] = state.rotation * rotation * Vector3.forward; 86 87 //-X 88 normals[normalsCount + 8] = state.rotation * rotation * Vector3.left; 89 normals[normalsCount + 11] = state.rotation * rotation * Vector3.left; 90 normals[normalsCount + 12] = state.rotation * rotation * Vector3.left; 91 normals[normalsCount + 15] = state.rotation * rotation * Vector3.left; 92 93 //+X 94 normals[normalsCount + 9] = state.rotation * rotation * Vector3.right; 95 normals[normalsCount + 2] = state.rotation * rotation * Vector3.right; 96 normals[normalsCount + 13] = state.rotation * rotation * Vector3.right; 97 normals[normalsCount + 6] = state.rotation * rotation * Vector3.right; 98 99 //-Y 100 normals[normalsCount + 16] = state.rotation * rotation * Vector3.down; 101 normals[normalsCount + 17] = state.rotation * rotation * Vector3.down; 102 normals[normalsCount + 18] = state.rotation * rotation * Vector3.down; 103 normals[normalsCount + 19] = state.rotation * rotation * Vector3.down; 104 105 //+Y 106 normals[normalsCount + 20] = state.rotation * rotation * Vector3.up; 107 normals[normalsCount + 21] = state.rotation * rotation * Vector3.up; 108 normals[normalsCount + 22] = state.rotation * rotation * Vector3.up; 109 normals[normalsCount + 23] = state.rotation * rotation * Vector3.up; 110 111 #endregion 112 113 #region Indices 114 115 int[] tmpIndices = new int[36] { 116 verticesCount + 0, 117 verticesCount + 5, 118 verticesCount + 1, 119 verticesCount + 0, 120 verticesCount + 4, 121 verticesCount + 5, 122 verticesCount + 9, 123 verticesCount + 6, 124 verticesCount + 2, 125 verticesCount + 9, 126 verticesCount + 13, 127 verticesCount + 6, 128 verticesCount + 10, 129 verticesCount + 7, 130 verticesCount + 3, 131 verticesCount + 10, 132 verticesCount + 14, 133 verticesCount + 7, 134 verticesCount + 8, 135 verticesCount + 15, 136 verticesCount + 12, 137 verticesCount + 8, 138 verticesCount + 11, 139 verticesCount + 15, 140 verticesCount + 20, 141 verticesCount + 22, 142 verticesCount + 21, 143 verticesCount + 20, 144 verticesCount + 23, 145 verticesCount + 22, 146 verticesCount + 16, 147 verticesCount + 18, 148 verticesCount + 19, 149 verticesCount + 16, 150 verticesCount + 17, 151 verticesCount + 18 }; 152 tmpIndices.CopyTo(indices, indicesCount); 153 154 #endregion 155 156 verticesCount += 24; 157 indicesCount += 36; 158 normalsCount += 24; 159 160 state.centerPos += state.rotation * (rotation * new Vector3(0, 1, 0) * growRate + centerPos); 161 state.rotation = rotation * state.rotation; 162 }
(为什么有24个顶点呢,是因为某个顶点根据三个所属面的不同,会有三条不同的法线。所以我把它们拆开了。
并且事实上只需要有verticesCount和indicesCount就行了,normalsCount,uvCount啥的不需要,它们实际上一定等于顶点数。不知道当时我在想什么hh)
这是一个类的成员函数,这个类代表分形结构中的某一个元素(线段,或者说是棍)。
(同时这个类是派生自一个"分型元素结点"的抽象基类)
而state中包含了当前的位置、旋转信息;对象的成员变量growRate代表了棍的大小。至于为什么这些参数要一部分放在state里一部分放在growRate里另有原因,不过之后就全放在对象的成员变量中了。
接下来我们来看一下它的基类。我们想要做的是一个分形系统,所以要能"产生细节"——即根据当前的细节产生下一级的细节。
这明显是一个树形结构,所以每个这种分型元素都有自己子节点(下一级细节)的指针,比如某个树枝上长出来的树杈。
1 abstract public class FractalSystemNode 2 { 3 public List<FractalSystemNode> child = new List<FractalSystemNode>(); 4 5 public