笔试题73. LeetCode OJ (60)

Posted 2020-07-20 _从未止步

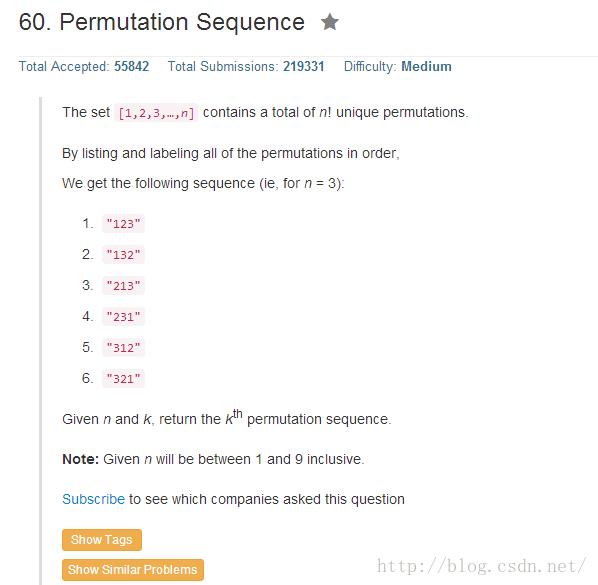
    Permutation Sequence

    这个题是求1~n (n[1~9]) 的数字的全排列的第K个序列。

    一般思路是：使用一个计数器，递归去找全排列序列，找到一个计数器加一，一直到第k个。

但是加若 n = 9 我要找的是第 （9! -1 ）个数，那么上述办法的时间是多少，多半会超时的（没试过，但是我敢保证一定会超时的，因为这样的思路不可取），想一想我们只需要一个序列，并不必要把全部的序列都找出来吧。下面我给出一种解题方案，我个人感觉是可取的。

    我们是学过数学的人，要我们求全排列的第 k 个序列，那么我们其实可以推测它的大致分布在那个范围（不是用眼睛看，而是推导出来的）。这个方法是这样的：

    假设 n = 3，那么 1~3 组成的全排列以及相应的第K个序列氛围如下：

k	n[1,3]
1	1  2  3
2	1  3  2
3	2  1  3
4	2  3  1
5	3  1  2
6	3  2  1

    首先说明一下像这种无重复数字的全排列规律：

    n = 1 时，全排列个数为： 1!

    n = 2 时，全排列个数为： 2!

    n = 3 时，全排列个数为： 3!

       .....

       基于这种规律我们是不是可以大致推测k的范围，推测的方法是去找一个数 m，时 m! > k，这样可以说明k的大致位置，画个图说一下思路吧。

     上面所说的解题方法确实不好描述清楚，因为它是数字规律，我是通过过滤一些位置来不断缩小k的值，当缩小到 k = 1的时候所对应的序列就是我们要找的序列，如果还没看懂的话那就是我没有描述好的问题了。所以我教一个方法：

例如：

当：n = 2

      1 2

      2 1

      那么我们交换1和2的位置(交换第一位和第二位的位置)，就相当于过滤掉一个序列了，k的值也就减小 1

当：n = 3

      1 2 3

      1 3 2

      2 1 3

      2 3 1

      3 1 2

      3 2 1

    所以当我们交换1和2的位置，我们就过滤了2个序列，相应的k的值也就减少了2，问题缩小为在两个数的全排列中寻找第k个序列

   当我们交换1与3的位置，我们就过滤掉了4个序列，相应的k的值也就减少了 4，问题也缩小为在两个数的全排列中寻找第k个虚列

   .... 所以这样就可以推导到 n = 4，5，6，7...，问题也就会不断缩小，最终缩小为1，问题解决，代码如下，可参考代码理解。

class Solution {
public:
	string getPermutation(int n, int k)
	{ //1~n 的全排列的 第k个数
		string ret;
		ret.clear();
		if (n == 1 && k != 1 || k > factorial(n))
		{
			return ret;
		}

		vector<int> v;
		v.clear();
		for (int i = 1; i <= n; ++i)
		{
			v.push_back(i);
		}

		int begin = 0;
		int pos = 0;

		while (k > 0)
		{
			begin = 1;
			int offset = 0;
			int nums = 0;

			while ((nums = factorial(begin)) < k)
			{ //k分布在第begin位之后
				++ begin;
			}
			nums /= begin;
			pos = n - begin;  //第pos位可能需要交换

			if (begin > n+1)
			{ //不存在，其实是越界了，意思是k比 n！还大，不存在
				return ret;
			}

			int temp = 0;
			int jump = 0;  //去找
			while (temp+nums < k)
			{ //去找需要和那一位交换位置
				temp += nums;
				++jump; //jump指明了该位置的相对距离
			}

			if (jump > 0)
			{
				swap(v[pos], v[pos+jump]);
				//交换位置后需要对后面的序列排序
				sort(v.begin() + pos + 1, v.end());
			}
            //交换后，k的相对位置发生变化
			k -= jump*nums;
		
			if (k <= 1)
			{ //这种情况说明此时就是要找的序列
				for (int i=0;i<n;++i)
				{
					ret.push_back(v[i] + '0');
				}
				return ret;
			}
		}
		return ret;
	}

	int factorial(int n)
	{ //求阶乘
		int ret = 1;
		for (int i = 2; i <= n; ++i)
		{
			ret *= i;
		}

		return ret;
	}	
};

结果如下：