排队理论解释TCP/IP网络拥塞是如何影响TCP的RTT的波动

Posted 2020-07-20 dog250

部门团建，大家都去长隆了，也有去澳门广西的...我去了梦里...本来我也报了名的，想单独带着女儿独处两天，不光为了培养跟女儿的感情，也是想让老婆歇两天...只可惜女儿最近生病，去不了了，六一儿童节的表演也由于生病被拒绝了，很是失落，更失落的是我，于是带着失落和愤怒，又有些许对不公道的无能的宣泄，我半夜爬起来，把这一切都诉诸给TCP/IP吧！
        就像上学时一样，大家临考前还在打牌，就我一个人在看书，结果他们就说我装，我就承认我装，但问题是，他们说完我装以后不到半小时，都去看书去了！我希望每个人都TMD装起来，气氛搞起来！周末全部用于学习和工作！即使下班回到家里也要支起摊子，学习和工作！永远别去旅游！永远不参加集体活动，99%的时间留给学习和工作！死的时候，嘴里喊着TCP/ip！忘掉女儿吧，忘掉家人吧，忘掉世界吧，从另一个维度观察这个令人XX的世界吧！

奇妙的世界

世界上很多事务都可以描述为正态分布，不管你信不信，事实就是如此，如果将这些事务细分，对于很多的离散的事件，均可以描述为泊松分布，不管你信不信，事实就是如此。不要试图去问“为什么世界上很多事实符合正态分布或者泊松分布？”，因为本来就是这个样子，在没有人出现之前就是这样，正态分布也好，泊松分布也好，正是人们找到的一种描述这种本质的一个“形容词”而已。

TCP发送端测量RTT的困惑

TCP的RTT到底可用吗？可用！只是很难发现规律而已。
人们天生有一种拔毛刺的习惯，脸上长个粉刺就要想法抠掉它，痣上长根毛也要拔掉它，看见谁爱出风头耍个性，就想千方百计整死他...如果看到测量的RTT波动很大，就非要想个算法把高值和低值去掉从而不看见它们，

Gaius Julius Caesar

不是说过吗， 人们总希望看到自己想看到的，那我就给他们！拿破仑也说过， 你不是个子高吗，我削除这个差别！都是带点血腥的，但是同时意味着只有少数人才能看到真相。
        根本就不该对RTT做任何假设，不但要关心它的稳定趋势，还要关心它的所谓毛刺！我相信波动的叠加，干涉，衍射是一个普遍的真理，任何事务都是有多个波叠加而成的，这些波具有不同的频率，波长，以及其它特性，我们需要做的就是分解它而不是试图湮没它。所以我从来不蔑视精神分裂患者，也不蔑视精神病人，因为这才是本质的，其它的都是装的，湮没过的。要想理解RTT的特点，要分两方面，一个是因，一个是果，原因呢，就是网络的行为，结果呢，自然就是发送端的行为了。

网络的行为

我们先来看一下网络上的数据包分组的行为，这是这种行为影响了TCP端到端的拥塞控制决策，网络行为是因，拥塞控制是果。

脆弱的队列

想当然的，我们会觉得路由器，交换机这种中间设备的队列(或者你可以直接认为是缓冲区)是一个缓解拥塞的有利设施，它可以缓解拥塞造成的后果。这么理解是对的，然而只对了一方面，如果我们直视问题，那么“拥塞”这个词是在有了“队列”这个设施以后才这么叫的，问题的本质在于“冲突”！两个数据包同时经由一个路由器，必然发生冲突，这意味着输掉的一方必须被丢弃，或者更惨烈的，两败俱伤。如果你对早期半双工总线以太网的CSMA/CD模型有足够深入的理解，就会明白这个事实。
        然而对于IP互联网，不能采用CSMA/CD这种机制，因为代价太高了，整个网络是如此之大，以至于即便使用不可超越的光速，冲突检测的时延也是不可忍受的，另一方面，节点是如此之多，以至于可以预想的冲突是多么地激烈！因此，互联网采用了另外一种措施，即冲突前仲裁，也就是引入了队列的概念，把自由争抢资源变成了有序复用资源。现实世界到处存在这种事实，比如两个人打架，随时开打，但是放眼到整个世界，就会有很多的规则。
        但是，这个队列是不稳定的，它不会像你想象的那样会优雅的为你提供冲突时的容身之地，而是会随着流量的增加随时崩溃，这就意味着端到端协议必须发现排队现象，以便采取措施缓解队列。对于路由器而言，它能采取的措施只有一个，就是丢弃数据包！
        在继续定量化分析之前，我们有必要来点排队论的知识，但一点点就够了。

排队理论

排队论是分组交换的核心，正是它使得分组交换替代电路交换成了可能。事实证明，分组交换的统计复用要比电路交换的固定X分复用(比如TDM)更加有效，也许，统计复用的背后可能就是见缝插针，然而排队现象的本质却不是见缝插针的结果，而是到达过程和服务过程的不均衡！到达过程是统计的，然而服务过程不能是统计的，它必须由到达过程来驱动，换句话说，到达的事件在受到服务可以排队但不能丢弃，而服务者宁可空转而不抢单！我后面会从一个悖论来详细说这个问题，最终的结论先给出：服务的效率必须高于到达率才能避免队列变成无限长！

        然而，现实世界更加复杂，我们国家总是看到服务部门效率远小于到达率，然而并没有看到永久队列...TMD不到下午4点就下班了，第二天再来吧！从而消除了队列！其实你问下随便排队的一个人，问他们排几天了，他们的回答会让你理解排队论。另外，即使你不能理解计算机内部的排队现象，那么去一下火车站售票口也行，或者，看看高峰期的大城市快速路高架桥...为什么队列没有永久加深，那是因为队列的清空是强制的。

       然而，为了讨论简单，我不谈现实，只谈理论情形，因此我不会引入任何路由器排队策略方面的东西。

泊松分布与指数分布

我们直接给出结论，数据包的到达过程中单位时间内到达数据包的数量是符合泊松分布的，由此可以推导出相邻数据包的到达间隔是符合指数分布的，这是自然界中奇妙统计规律的体现。
        如果直观地理解这两个分布，非常简单，统计学中有个中心极限法则，意思是每个事务都有一个中心，即平均点，越偏离中心的概率越低，比如人类的平均身高是1.75cm，这意味着你将很难找到2.5cm或者0.5cm的人。对于指数分布，可以这样理解，如果你去一家公司面试，过了一天没有给你打电话，过了三天还是没有给你电话，那么你此后接到电话的几率将迅速降低，这是合理的，一般而言，对于如意的人，招聘方会在很短的时间通知你的。

M/M/1排队模型

排队论非常复杂，本文的目的仅仅是为了帮助理解TCP在拥塞时RTT的变化情况以及发送端的反应，因此并不准备深入排队论内部，这部分内容在研究路由器行为时显得更加重要(写到这里...又让我想起了去年的事，想起了华为...)。
M/M/1模型属于排队论里描述普遍情况的最简单的一种，第一个M代表到达过程服从泊松分布，第二个M代表服务过程符合负指数分布(由到达过程驱动，前后被服务对象无关联)，第三个1表示只有一个服务者。整体的过程逻辑上如下图所示：

到达过程
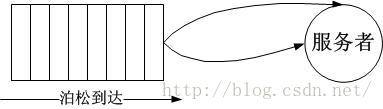
按照时间序列展开，到达过程可以直观地描述成下面的样子：

我们设到达率##，意味着##只是一个“平均数”，只是说这个到达过程中单位时间到达##的可能性很大，但偶尔也会在单位时间内到达多于##或者少于##，这个务必要记住，因为这是引起排队的比较重要的原因。
服务过程
服务过程比较简单，说它是一个指数分布是因为它是受到到达过程驱动的，由泊松分布的理论我们知道到达过程中两件事到达的时间间隔符合指数分布，对于服务过程来讲，它服务的正是到达的事件，因此服务的间隔就是到达的间隔，所以它是符合指数分布的。
        你可以把服务过程看作是一个不停轮转的传送带上的一个机械手臂，它没有智能，只会不停地试图抓取传送带上的物品，如果没有物品，就空抓一次，有的话就抓取到旁边的框子里。它抓到物品的时间间隔符合指数分布。理解了这一点，有助于理解我后面给出的一个悖论的解释。

排队分析

我们直接给出根据M/M/1排队模型得到的结论，并没有任何关于这个结论的推导过程，这不是本文的核心，事实上推导非常简单。

(1).排队数据包的数量

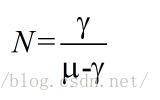
(2).排队数据包的等待时延

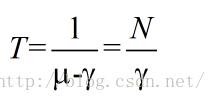
(3).每一个数据包的等待时延

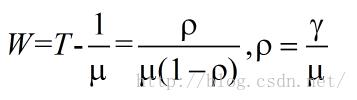
(4).平均队列长度

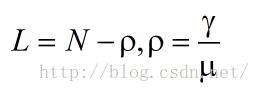
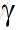通过上述的(1)可以看出，如果 和 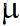的比值小于接近1，N将会趋向于无穷大，这意味着若不想让队列无限制挤压，服务率必须大于到达率才可以，我们再看另一个极端，N为1的时候，也就是说仅仅有自己排队(可以近似为没有队列)的情形，算出来服务率必须是到达率的2倍！也就是 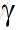和 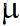的比值为1/2，我们看一下(1)关于N和 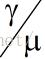比值的图像：

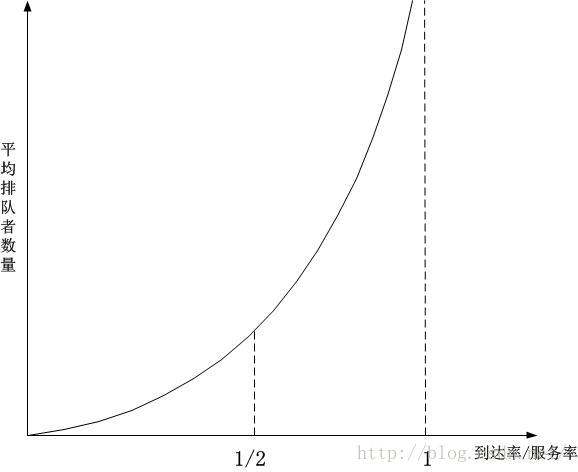
发现上述比值在1/2和1之间的时候，曲线逐渐抖上去了，这意味着，只要到达率稍微增加一丁点，排队者的数量将迅速增加(对比(4))，如果此时发送方再不降低速率甚至增加速率，队列将无限制增加，网络将崩溃。

        于此同时，我们看一下(3)，随着到达率的增加，和排队者一样，队列中数据包的排队时延也将迅速增加！这就是为什么TCP数据采集到RTT波动特别大的原因，RTT并不会无缘无故地波动，原因几乎都是发生了拥塞，而波动的幅度和持续时间，受到了路由器的排队策略的影响，这意味着何时缓解拥塞将决定RTT的波动曲线！

        至于说路由的队列管理，并不是本文的内容范围，可以简单说一下，路由器可以简单的进行尾部丢弃，也可以进行随机丢弃，可以基于数据包特征进行优先级排队，更复杂的内容可以自行google关于“主动队列管理(Active Queue Management，AQM)”的内容。
        正是由于存在路由器的队列管理，现实世界中，网络才不至于崩溃，因为路由器不允许队列无限长。在发现有队列即将暴涨的预兆之后，路由器就会采取措施了，这种措施的结果会反馈到数据包的发送端，由该发送端自行决策如何反应，在接着这部分之前，我们先来看一个好玩的悖论。

一个悖论

我想通过一个悖论来描述一下以上排队分析这背后的原因，仅从数学上看，它确实如此，但这并不意味着真正的理解，理解了背后的原因后，你可能不一定需要数学工具就能解释这一切，我相信任何复杂的理论背后都有一个不需要数学来解释的原因。
        在前面的讨论中，我们知道数据包的到达率和服务率之比为1的时候，队列长度将无限大！这不符合常理啊，如果说到达率为a，服务率也是a，这不正是守恒吗？来一个处理一个，怎么可能挤压呢？另外，到达率和服务率之比的这个1/2是怎么来的呢？
在我想阐释这个悖论前，和以往一样，先看看有没有现成的解释，于是发了一个知乎上不错的解释，也就省了我打字画图的时间了，链接如下《 poisson到达的一个悖论怎么解释？》。看明白了吗？
        我这里再给出另外一个解释，我这里基于令牌守恒的原理来解释，希望能有所帮助。

附：令牌守恒解释排队论的悖论

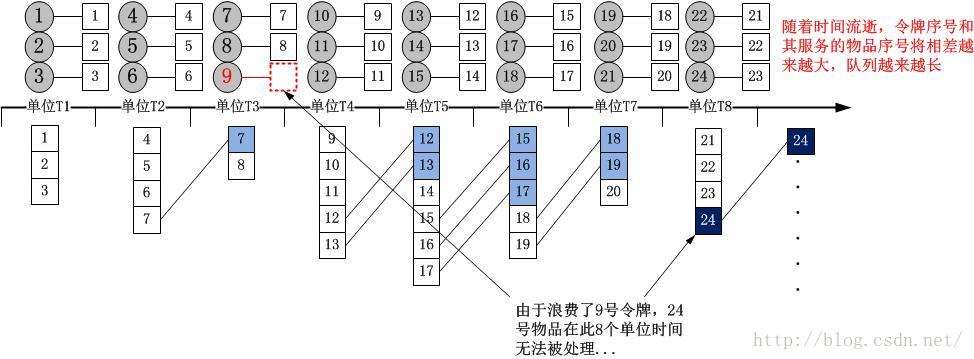
我将到达过程和服务过程想象成物品的涌入过程以及令牌的发放和回收过程：
到达过程--物品按照速率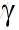到达一个时间序列，单位时间到达的物品量符合泊松分布。
服务过程--服务者按照固定速率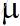在时间序列上发放令牌，如果该点上有物品(不管多少个)，则最多带走一个物品(因为只放一个令牌)，如果没有物品，则空放一个令牌。
我用一个图来举一个例子吧！把足够长的时间缩短到一个有限的时间，假设到达率为3，服务率也是3，到达率符合离散的正态分布(泊松分布也是一样的结果，这里强调的只是，到达过程是统计的，而不是匀速的)，时间段为8个单位时间，有了以上的假设，我们知道这段时间服务者会匀速放出3*8=24个令牌：

随着时间流逝，队列会越来越长，造成这种现象的原因在于，队列的积压和排空是不对称的，服务方比到达方要强势的多！对于到达方而言，如果恰好没有服务方，就要安静地排队，而对于服务方而言，如果没有到达方，它只是空转，要知道，空转是需要能量的！这是因为，到达的事件必须要被服务。(其实，在银行大厅，你会发现不管有没有客户，总有服务台有办事员等待，他们是要领工资的...这就是排队的本质，到达方和服务方不对等！！)
        这就是所谓的统计波动。有时候，这种效应可以跟短板效应(木桶)等价起来，这个在艾利.高德拉特的《 目标》一书中也有阐述，意思是最慢的环节决定总体进度，我的理解就是：一步错，步步错！功不抵过！哈哈。
        从这个悖论的分析可以看出网络节点的队列确实很脆弱，一不小心就排队了，而且这个队列在持续恒定到达率下几乎不会被清空，反而会增长，这可能不太符合常识，但是统计学表明确实如此，要想清空队列，必须减小到达率，或者动态增加服务率，也就是增加处理的功率。
        结论是什么呢？结论就是，排队很容易发生，然而队列的清空却很难！在M/M/1模型中，可以证明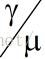， 的值大于0.8的时候，队列就会快速增长到一个很长的稳定值。

        好了，目前为止，我们对网络中间的行为的已经理解得很透彻了，虽然只用了简单化的M/M/1模型进行了分析，而事实上真实网络上的模型要复杂的多，然而这对于理解问题的本质已经够了。接下来我们要分析TCP发送端的反应了。这个反应非常重要，因为队列的清空也就是拥塞的缓解，几乎完全依赖与这种发送端的反应！

TCP端到端的行为

我们可以把TCP的拥塞控制机制看作是对上述网络行为反馈的反应。反应或许可以分为三种，要么激进，要么保守，要么无视之，但不管怎样，TCP总是要对自己的反应付出代价，或者取得收益。
        要知道的是，TCP的发送端对网络现状的了解总是有一些滞后性，就像CSMA/CD一样，网络拥塞信号传递到发送端最少要经过半个RTT的时间，经常会更久，我们知道，TCP发送端的数据发送是靠接收端的ACK来驱动的，即便在接收端附近发生了拥塞，数据包发生了排队现象，从排队开始到排队结束的时间(假设没有发生丢包)，加上ACK返回发送端的半个RTT时间，总的拥塞信号反馈时间就是半个RTT加上排队时间，而排队时间我们可以从上一节排队论分析中的公式(3)平均等待时延中得到，这个过程的时延将决定性地取决与排队时延！如下图所示：

对于TCP发送端而言，它会发现RTT变长了，事实上这个变长就是因为排队引发的。发送端会根据这个RTT的反馈信号调整自己的行为，为了更加精确的反省(我没有用预测这个词，因为此时拥塞已经发生了)网络中到底发生了什么，对RTT测量值的统计是必要的，这就是我们接下来的内容。

抖动与噪点

如果观察TCP发送端采集到RTT分布，会发现其波动性特别大，有时候RTT会异常升高，好像魔法一样...如果理解了排队时延公式的含义，就会很容易理解这个现象了，因为拥塞发生的时候，即便稍微增加一点流量(这意味着到达率的升高或者仅仅意味着路由器端口的服务率不是到达率的2倍，造成恒定的平均队列长度的在均值上下波动)，也会造成瞬时的排队时延增加。如何从这些采样值中看出一些端倪呢？比如说这些采样值的抖动是持续拥塞导致还是偶尔的突发流量造成的时延噪点呢？就需要从这些采样值中规划出某种趋势。在持续拥塞时，RTT表现为持续保持高值或者随着队列长度的加长而快速升高，然而在面对突发流量造成的排队拥塞时，这些RTT表现为某些高值噪点。我们总不能用肉眼来观察这些海量数据，因此需要某种计数来将这些表现归纳到某个数值代表的趋势中，这就涉及到了低通滤波器的运用。

低通滤波

所谓的低通滤波的目的就是消除噪点震荡，在模拟电路中，我们可以采用一个电感来实现，而对于高通滤波，则使用电容可以实现。这个在统计趋势的时候怎么做到呢？无外乎就是做到以下两点：
1).如果这是一个持续的高值或低值，积累它；
2).如果这是一个偶尔的高值或低值，平滑它；
为了表达一种趋势，这个滤波器必然是一个有状态的设施，它可以将历史值加权累加到当前值之上，以表达历史的的趋势。如今，应用比较广泛的一个低通滤波器就是加权指数平均值，也叫做移动指数平均值。

移动指数平均的意义

首先给出公式：
V=(1-a)*V+(a)*Vnew
这实际上是一个递推得来的式子，起初，V0是一个初始值x
V0=new0
V1=(1-a)*V0+a*new1=(1-a)*new0+new1
V2=(1-a)*V1+a*new2=(1-a)^2*new0+(1-a)*new1+a*new2
V3=(1-a)*V2+a*new3=(1-a)^3*new0+(1-a)^2*new1+(1-a)*new2+a*new3
V4=(1-a)*V3+a*new4=(1-a)^4*new0+(1-a)^3*new1+(1-a)^2*new2+(1-a)*new3+a*new4
V5=(1-a)*V4+a*new5=(1-a)^5*new0+(1-a)^4*new1+(1-a)^3*new2+(1-a)^2*new3+(1-a)*new4+a*new5
....
V[n]=(1-a)*V[n-1]+a*Vnew=(1-a)^n*new0+(1-a)^[n-1]*new1+(1-a)^[n-2]*new2+(1-a)^[n-3]*new3...a*Vnew[n]
可以看到，某次的瞬时值Vnew[n]的作用随着时间的推荐指数级递减，然而另一方面，它的递减值确实是积累性的，这就既可以平滑掉瞬时值的作用，又可以将该瞬时值成为历史值后做累加，最终的结果就保证低通滤波器要求的那两点。
        可以看出，关键在于系数a的选择，这个a越大，表明瞬时值的影响越大(即便再大，也会被时间所遗忘)。a的取值一方面靠分析，一方面靠经验和运气！

RTT和RTO的计算

有了上面的利器，我们可以应付抖动的RTT了，当前主流的TCP实现中，均采用了上述的移动指数平均来计算RTT和RTO，RTT具体的算法就不说了，至于说瞬时RTT采样的权值为什么是1/8，应该是调得一手好参数的经验值吧。
        重点是RTO的计算，我们知道，RTO要比RTT略长一点，那么到底长多少呢？早期的算法很简单，就是RTT乘以一个大于1的系数，但是即便是平滑过的RTT反映了正常的拥塞排队情况，也无法反映是瞬时突发队列还是长期竞流导致的拥塞队列，因为这涉及到一个动态的过程。这是为什么呢？为什么无法反映呢？
        因为我们自己在计算RTT的时候用移动平均算法将这种动态特征过滤掉了！这就是所谓“低通”的含义！！低意味着频率低，也就是稳定的意思，而高则意味着频率高，也就是抖动的含义。RTT到底该不该平滑掉动态特性呢？这要分两个方面说：
对于指导窗口的调整：应该平滑掉动态特征
对于设置RTO：恰好要利用其动态高频特征
RTO不能设置的比合理值大，这样会降低性能，也不能比合理值小，这样会增加不必要的重传，恰恰用以下的原则来指导，如果RTT波动大，则设置的要大一点，如果波动小，就要设置的小一点。
        这就正如除法得商取余数一样美妙，什么也不浪费，即使平滑掉了RTT的抖动，也可以再为其抖动特征求个标准差！
        求RTT瞬时采样值和移动指数平均的RTT做差，然后对此差值做移动指数平均作为设置RTO的标准。几乎任何讲网络的书上都有这个，我不再重复书上的内容了。

FAST TCP对RTT的合理化优化

虽然我们知道，RTT在做移动指数平均的时候，1/8是一个奇妙的数字，“不知道怎么来的，但是就是可以工作的很好！”，然而还是受到了挑战。FAST TCP并不认为1/8是一个永恒的系数，它有其自己的算法，在一个草案《FAST TCP for High-Speed Long-Distance Networkshttps://tools.ietf.org/html/draft-jin-wei-low-tcp-fast-00》中，它给出了：
4.2 avgRTT Computation

   In [VJ88], the average weight for Exponential Weighted Moving Average
   (EWMA) is 1/8. For high-speed long-distance network, smaller average
   weight is recommended since, with a large window, successive RTT
   samples capture congestion information over a timescale that is much
   smaller than a RTT.  Average RTT values should capture the state of a
   network during the last window.   We suggest an average weight that
   is proportional to the reciprocal of cwnd:

      weight = min{ 3/cwnd, 1/8 }

   The average RTT is updated on the receipt of a new RTT sample,
   as follows:

      avgRTT_new = (1-weight)*avgRTT_old + weight*RTT
      
因此可以看到，它不光把RTT作为了网络拥塞判断的指标，还把窗口因素也算进去了，某种意义上，由于窗口在很短的时间间隔内不会陡升陡降，可以代表着上一次发送时的网络情况，将这个和历史的avgRTT_old就行加权是一个很好的想法，因为这里面有一种Bloom Filter的意思。
        如果一个判断无法判断出一个趋势，那就找几个正交的判断一起来吧，如果这些判断同时或者起码绝大多数结果都反映了同一个趋势，那就说明这个趋势是一个必然的趋势！

回到开始

我们回到开始Gaius Julius Caesar和拿破仑的话，我们看看 真实的RTT和 人们想看到的RTT：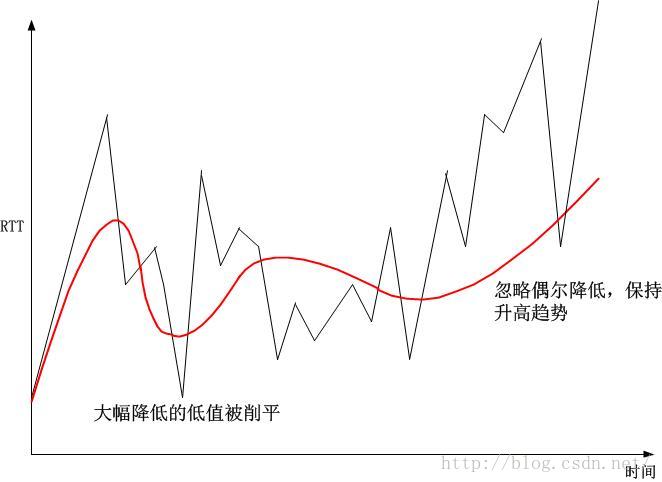

                            --------------------------------------------- 矛盾！虚伪！贪婪！欺骗！好强！无奈！简单！善变！孤独！气愤！得意！伤感！怀恨！报复！专横！责难！

                                                                                                                                                           公元2016年6月4日，上午 10点05分！儒略历（有误，没时间仔细研究）