LintCode数组题总结
Posted 月光下的夜曲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LintCode数组题总结相关的知识,希望对你有一定的参考价值。
做算法题的时候,几乎不可避免要跟数组打交道。在LintCode上数组那一章有这么一些题目:
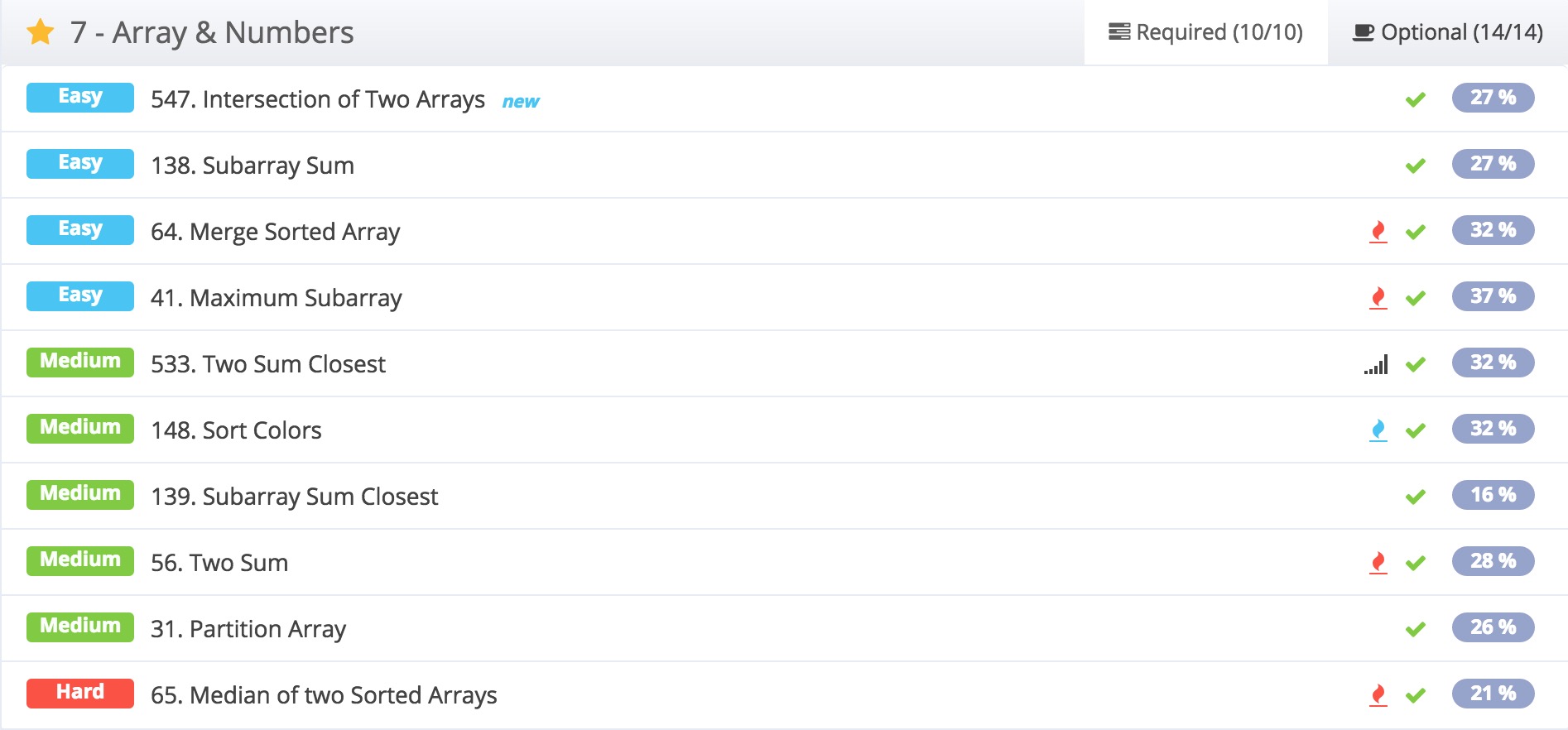
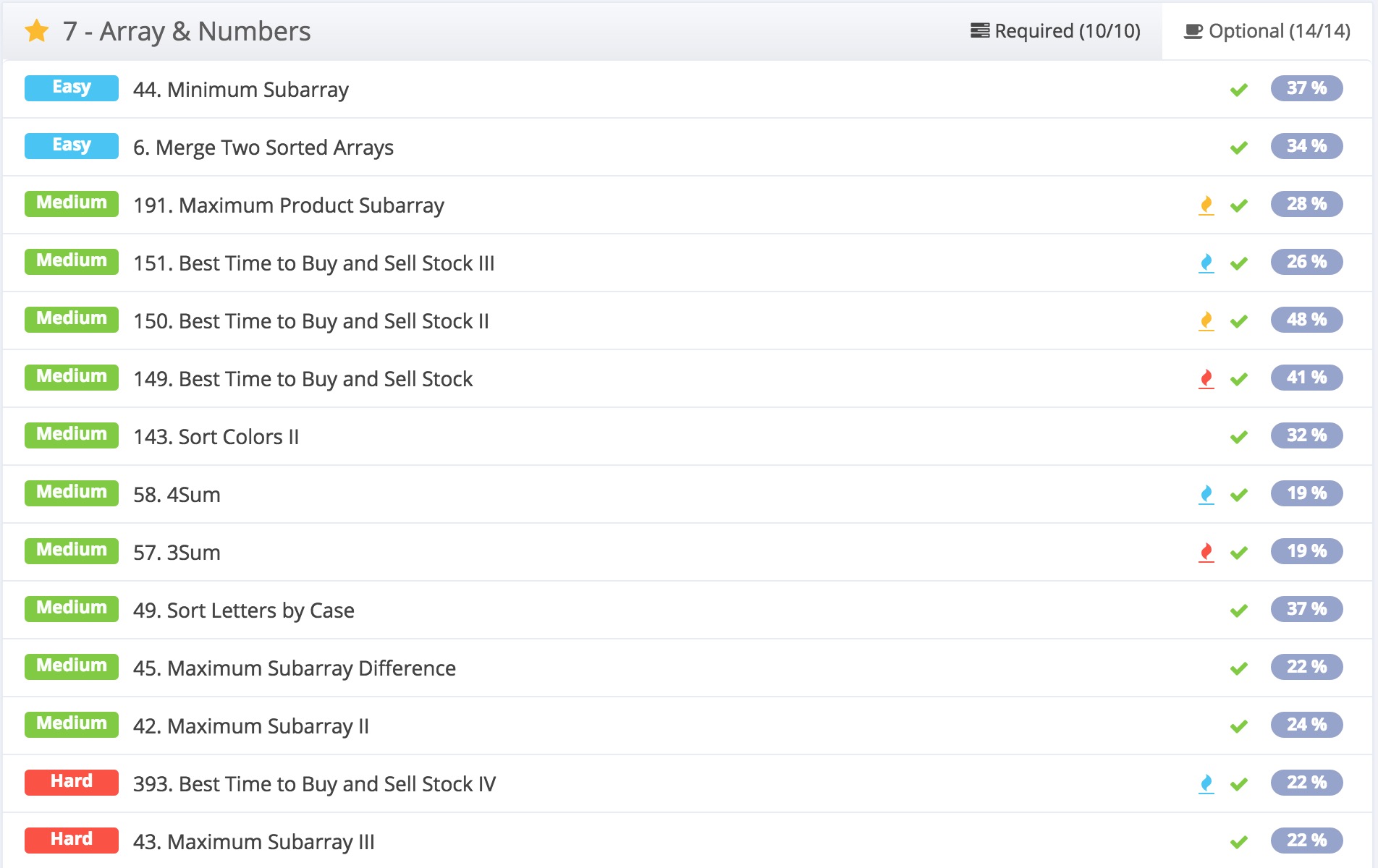
1)547. Intersection of Two Arrays
比较简单。要求找到2个数组的交集,简单点的方法就是用2个hashSet,第一个HashSet存第一个数组的元素。然后扫描第二个数组,如果第二个数组中的元素在第一个HashSet中出现了,那么就把它加到第二个HashSet中。最后第二个HashSet就是两个数组的交集了。
比较简单。对两个数组进行merge,新开一个数组,从后往前扫描。两两比较,较大的加到尾部。最后如果2个数组有剩余,则把剩余的元素也加进去。
3) 64. Merge Sorted Array
比较简单。对2个有序数组A和B进行合并,要求把B合并进A,因为A数组尾部有足够的空间可以容纳B。建议从后往前扫描,这样的代码更加简洁。扫描完了后看B数组有没有剩余,若有剩余则把剩余的元素也添加到A数组头部。代码如下:
public void mergeSortedArray(int[] A, int m, int[] B, int n) {
while (m >= 1 && n >= 1) {
if (A[m - 1] >= B[n - 1]) {
A[m + n - 1] = A[m - 1];
m--;
} else {
A[m + n - 1] = B[n - 1];
n--;
}
}
while (n > 0) {
A[m + n - 1] = B[n - 1];
n--;
}
return;
}
数组中的元素只有0、1、2这三个类型的数字,要求对他排序。Given [1, 0, 1, 2], sort it in-place to [0, 1, 1, 2]。官网提示了一种naive的做法:A rather straight forward solution is a two-pass algorithm using counting sort. First, iterate the array counting number of 0's, 1's, and 2's, then overwrite array with total number of 0's, then 1's and followed by 2's. Could you come up with an one-pass algorithm using only constant space?
但是得循环2次,有没有办法只用一次循环搞定呢?那就得用双指针法了。
从数组两端向中间遍历,前面放0,后面放2。把前面出现的2放到后面,后面出现的0放到前面,这样中间剩下的就是1
我的解法是定义指针start = 0,指针end = n - 1;一次遍历,如果遇到0,交换给start,遇到2,交换给end,遇到1别管。代码如下:
public void sortColors(int[] nums) {
int start = 0, end = nums.length - 1;
int index = 0;
while (index <= end) {
if (nums[index] == 0) {
swap(nums, index, start);
index++;
start++;
} else if (nums[index] == 1) {
index++;
} else {
swap(nums, index, end);
end--;
}
}
}
private void swap(int[] nums, int a, int b) {
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}算法的关键在于,当从前往后扫描数组的时候,把0往最左边放,把2往最右边放。
当index对应的元素是0时,就把它和start交换,往前面放。因为是从左往右扫描的,所以每次遇到0都往左边放,这样能够保证左边都是0。
当index对应的元素是1时,直接继续扫描,不用管它。(因为在之后的扫描会把这个1变为0或者维持1不变)
当index对应的元素是2时,我们把它与end交换后,只需要把end指针往左边挪一位,而不用给index++。但是当index对应的元素是0时,我们却要给index++。这是为啥呢。
原因在于,index对应的值为2时,end对应的值也可能为2,在这种情况下,交换完了之后,index自己还是2,所以不行,index还的继续留在这个位置;
新开一个数组,用于记录1到k出现的次数,然后再根据出现的次数把这些数字写回原数组。时间复杂度为O(n)。以空间换时间。
public void sortColors2(int[] colors, int k) {
int[] kArray = new int[k + 1];
for (int i = 0; i < colors.length; i++) {
kArray[colors[i]]++;
}
int index = 0;
for (int i = 1; i < kArray.length; i++) {
while (kArray[i] > 0) {
colors[index++] = i;
kArray[i]--;
}
}
}给定一个target,要求在数组中找到两个数之和等于target,并返回这两个数的下标。最简单的是2层循环嵌套暴力求解O(n^2),稍微好一点的解法是先排序,然后再在排好序的数组中从两边往中间扫描,如果找到2个数之和等于target,就在原数组中扫描找到它们原来的下标并返回,时间复杂度是O(nlog(n)),代码如下:
public int[] twoSum(int[] nums, int target) {
int[] res = new int[]{-1, -1};
int[] oldNums = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
oldNums[i] = nums[i];
}
Arrays.sort(nums);
int left = 0, right = nums.length - 1;
while (left < right) {
if (target - nums[left] == nums[right]) {
res[0] = nums[left];
res[1] = nums[right];
break;
} else if (target - nums[left] < nums[right]) {
right--;
} else {
left++;
}
}
int[] toReturn = new int[2];
for (int i = 0; i < oldNums.length; i++) {
if (oldNums[i] == res[0]) {
toReturn[0] = i + 1;
break;
}
}
for (int i = 0; i < oldNums.length; i++) {
if (oldNums[i] == res[1] && i != toReturn[0] - 1) {
toReturn[1] = i + 1;
break;
}
}
Arrays.sort(toReturn);
return toReturn;
}
我的目标是要找到a+b=target中的a和b,从左往右扫描数组,每次都把target-a加进map中,同时每次都在map中寻找看target-a存不存在:
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; i++) {
if (map.get(nums[i]) != null) {
res[0] = map.get(nums[i]) + 1;
res[1] = i + 1;
}
map.put(target - nums[i], i);
}
return res;
}以上是关于LintCode数组题总结的主要内容,如果未能解决你的问题,请参考以下文章