对”堆”的理解

Posted 2020-07-20 Liberal-man

对”堆”的理解

• 向下调整
• 向上调整
  堆是一种特殊的完全二叉树，至于什么是完全二叉树自己搜吧，这里就不讲了，看图：
  

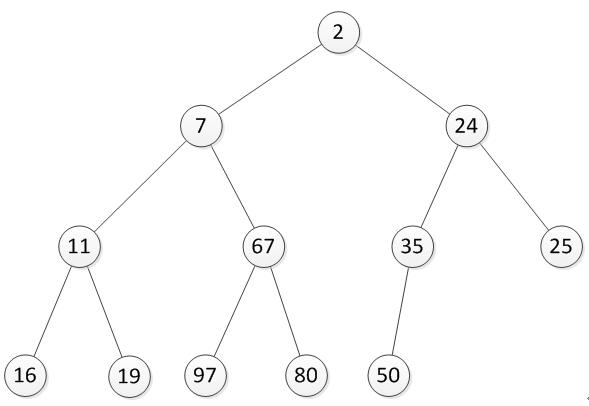
如上，所有父结点都比子结点要小，符合这样特点的完全二叉树我们称为小顶堆。反之，如果所有父结点都比子结点要大，这样的完全二叉树称为大顶堆。那这一特性的实际意义是做什么呢？
假如有12个数分别是80、7、35、24、19、50、11、2、16、25、67、97，要找出这12个数中最小的数，请问怎么办呢？最简单的方法就是将这12个数从头到尾依次扫一遍，用一个循环就可以解决。这种方法的时间复杂度是O(12)也就是O(N)，如下，灰色部分就是相关算法：
如下，灰色部分就是相关算法：

#include <stdio.h>
#include <limits.h>
int main(){
    int A[] = { 80, 7, 35, 24, 19, 50, 11, 2, 16, 25, 67, 97};
    int i = 0, min = INT_MAX; // INT_MAX 表示无穷大
    for (i = 0; i < sizeof(A)/sizeof(int); i++){
        if (A[i] < min)
            min = A[i];
    }
    printf("%d\\n", min);
    return 0;
}

输出结果：2
现在我们需要删除其中最小的数2，然后增加一个新数17，再次找这12个数中最小的一个数。请问该怎么办呢？按上一步的方法，扫描所有的数，找到新的最小的数，这个时间复杂度也是O(N)。假如现在有12次这样的操作（删除最小的数后并添加一个新数）。那么整个时间复杂度就是$12*O(12)=O(144)$即$O(N^2)$。那有没有更好的方法呢？堆这个特殊的结构恰好能够很好地解决这个问题。
首先我们先把这个12个数按照最小堆的要求放入一棵完全二叉树：

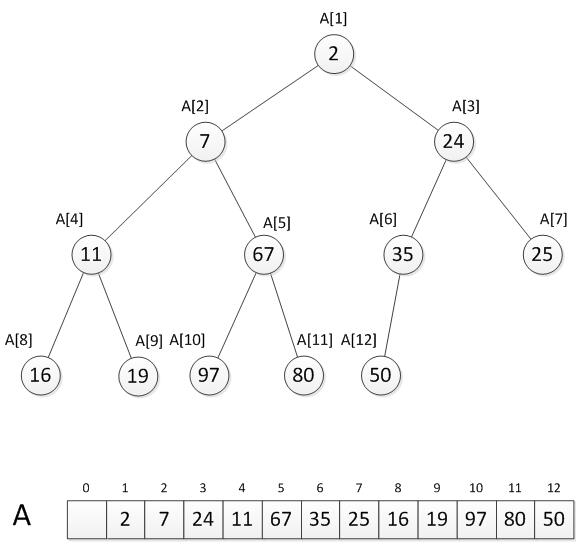
注意：我们这里，堆在程序中的保存方式，是用一个线性数组来存储的，比如数组A[N]。实际存储数据的时候，我们数据的排列起点是从A[1]开始的，A[0]没有使用，置空，主要是为了便于直观理解算法，降低复杂度。A[1]就是堆顶，A[i*2]就是其左孩子，A[i*2+1]就是其右孩子(i=1)。

很显然最小的数就是堆顶A[1]位置的2。接下来，我们将堆顶的数替换为17。新数已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。那如何调整呢？

向下调整

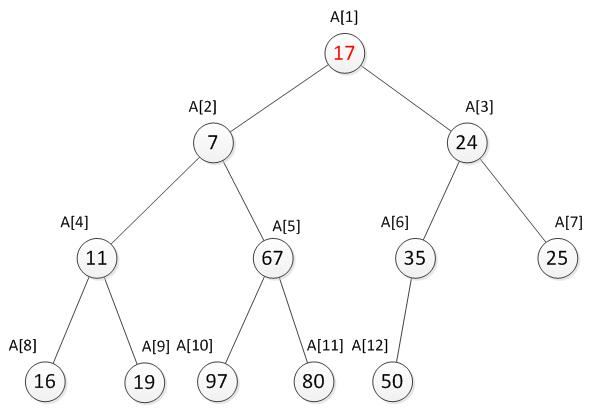
我们需要将17与它的两个儿子7和24比较，并选择较小一个与它交换，交换之后如下。

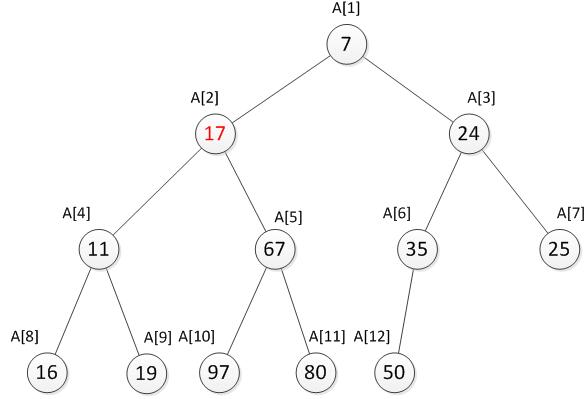
我们发现此时还是不符合最小堆的特性，因此还需要继续向下调整。于是继续将17与它的两个儿子11和67比较，并选择较小一个交换，交换之后如下。

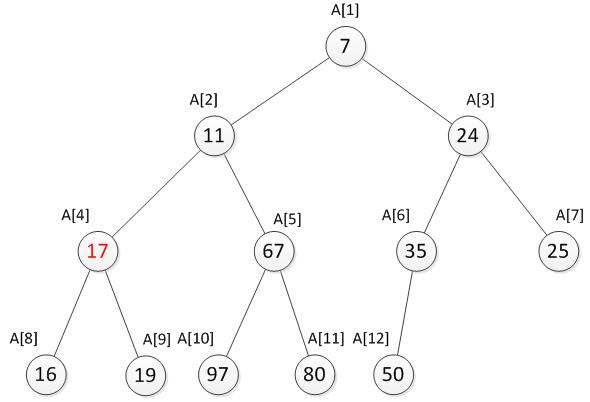
到此，还是不符合最小堆的特性，仍需要继续向下调整直到符合最小堆的特性为止。

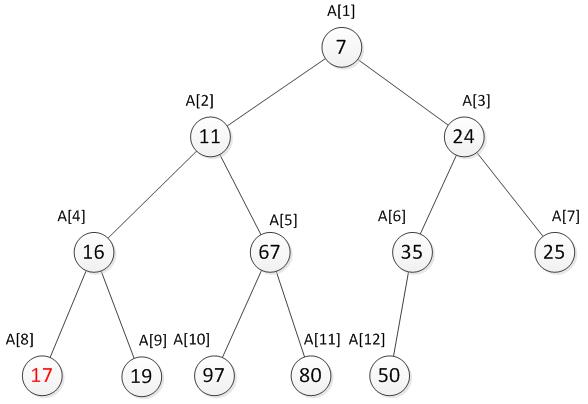
我们发现现在已经符合最小堆的特性了。综上所述，当新增加一个数被放置到堆顶时，如果此时不符合最小堆的特性，则将需要将这个数向下调整，直到找到合适的位置为止，使其重新符合最小堆的特性。

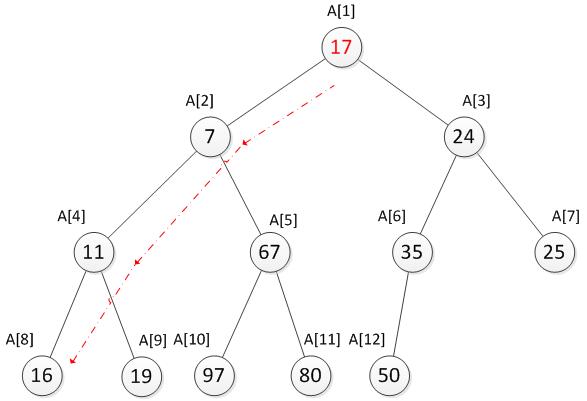
向下调整的代码如下，godown函数是调整的实现：

#include <stdio.h>
#define N 12
void printHeap(int A[]){
    printf("            -----------%d-----------\\n", A[1]);
    printf("           /                       \\\\\\n");
    printf("      ----%d----               ----%d----\\n", A[2], A[3]);
    printf("     /          \\\\             /          \\\\\\n");
    printf("  --%d--     ---%d---     ---%d          %d\\n", A[4], A[5], A[6], A[7]);
    printf(" /      \\\\   /        \\\\   /\\n");
    printf("%d      %d %d        %d %d\\n", A[8], A[9], A[10], A[11] , A[12]);
}
void swap(int A[], int t, int i){
    A[t] = A[t] ^ A[i];
    A[i] = A[t] ^ A[i];
    A[t] = A[i] ^ A[t];
}
/* 向下调整。
 * @param A 堆的线性存储方式，数组
 * @param n 节点总数
 * @param i 需要向下调整的节点编号
 */
void godown(int A[], int n, int i) //传入一个需要向下调整的结点编号i，这里传入1，即从堆的顶点开始向下调整 
{
    int t,flag=0,count=0;//flag用来标记是否需要继续向下调整 
    //当i结点有儿子的时候（其实是至少有左儿子的情况下）并且有需要继续调整的时候循环窒执行
    while( i*2<=n && flag==0 )
    {        
        //首先判断他和他左儿子的关系，并用t记录值较小的结点编号 
        if( A[i] > A[i*2] )
            t=i*2;
        else
            t=i; 
        //如果他有右儿子的情况下，再对右儿子进行讨论 
        if(i*2+1 <= n)
        {
            //如果右儿子的值更小，更新较小的结点编号  
            if(A[t] > A[i*2+1])
                t=i*2+1;
        }
        //如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的  
        if(t!=i)
        {
            swap(A, t, i);//交换
            i=t;//更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整
            printf("\\n\\n第 %d 次调整堆：\\n", ++count);
            printHeap(A);
        }
        else
            flag=1;//则否说明当前的父结点已经比两个子结点都要小了，不需要在进行调整了,退出
    }
}

int main(){
    int A[N+1] = { 0, 2, 7, 24, 11, 67, 35, 25, 16, 19, 97, 80, 50}; // 这里为了直接展示调整堆算法，直接给出已经建好堆的数组，免去建堆这一步，A[0]是不使用的，堆从A[1]开始。
    printf("初始化堆:\\n");
    printHeap(A);
    A[1] = 17; // 测试，修改堆顶值
    printf("\\n\\n修改堆顶值为17:\\n");
    printHeap(A);
    godown(A, N, 1);
    return 0;
}

我们刚才在对17进行调整的时候，竟然只进行了3次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶为7。之前那种从头到尾扫描的方法需要12次比较，现在只需要3次就够了。现在每次删除最小的数并新增一个数，并求当前最小数的时间复杂度是O(3)，这恰好是$O(log_2 12)$即$O(log_2 N)$简写为$O(log N)$。假如现在有10000个数，进行1万次替换最小数的操作，使用原来扫描的方法计算机需要运行大约10000*10000=1亿次；而现在只需要$N*log N$次(N=10000)，即14*10000次=14万次(214=16384，所以$log 10000$的对数值大概是14)。从亿到几万的量级跨度，可是跌了不少啊，那么算下节省了 (1亿次/14万次) 约是7百多倍的计算量，这可是巨大的优化啊。
看下上面程序的运行结果：

向上调整

说到这里，如果只是想新增一个值，而不是替换或者删除最小值又该如何操作呢？即如何在原有的堆上直接插入一个新元素呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为N（即有N个元素），那么插入一个新元素所需要的时间也是$O(log N)$。例如我们现在要新增一个数15。

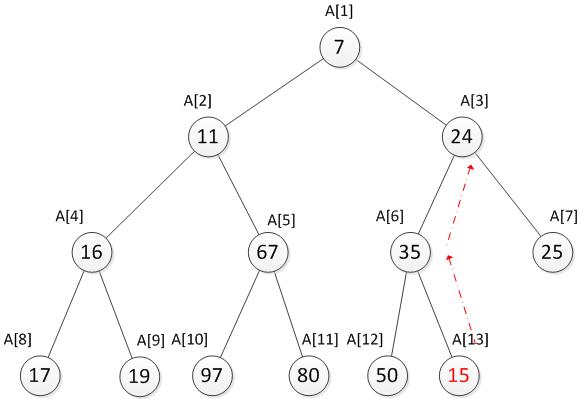
先将15与它的父结点35比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点24小，因此需要再次与父结点交换。至此又重新满足了最小堆的特性。向上调整完毕后如下。

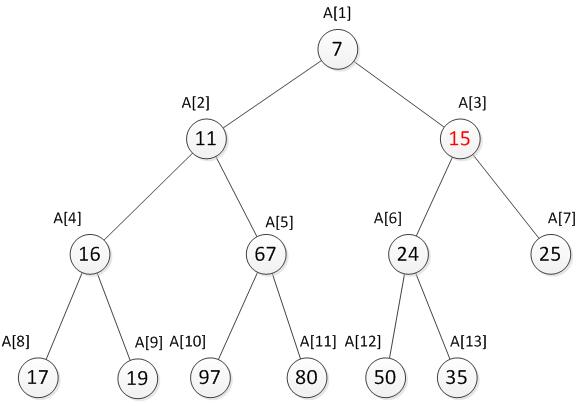
向上调整的代码goup函数如下。：

#include <stdio.h>
#define N 13
void printHeap(int A[]){
    printf("            -----------%d-----------\\n", A[1]);
    printf("           /                       \\\\\\n");
    printf("      ----%d-----               ----%d----\\n", A[2], A[3]);
    printf("     /          \\\\             /          \\\\\\n");
    printf("  --%d--     ---%d---     ---%d          %d\\n", A[4], A[5], A[6], A[7]);
    printf(" /      \\\\   /        \\\\   /\\n");
    printf("%d      %d %d        %d %d\\n", A[8], A[9], A[10], A[11] , A[12]);
}
void printHeap1(int A[]){
    printf("            -----------%d-----------\\n", A[1]);
    printf("           /                       \\\\\\n");
    printf("      ----%d-----               ----%d----\\n", A[2], A[3]);
    printf("     /          \\\\             /          \\\\\\n");
    printf("  --%d--     ---%d---     ---%d---       %d\\n", A[4], A[5], A[6], A[7]);
    printf(" /      \\\\   /        \\\\   /        \\\\\\n");
    printf("%d      %d %d        %d %d        %d\\n", A[8], A[9], A[10], A[11] , A[12], A[13]);
}
void swap(int A[], int t, int i){
    A[t] = A[t] ^ A[i];
    A[i] = A[t] ^ A[i];
    A[t] = A[i] ^ A[t];
}
/* 向上调整。
 * @param A 堆的线性存储方式，数组
 * @param n 节点总数
 * @param i 需要向上调整的节点编号
 */
void goup(int A[], int n, int i) //传入一个需要向上调整的结点编号i
{
    int flag=0, count = 0; // flag用来标记是否需要继续向上调整
    if(1 == i)  return; //如果是堆顶，就返回，不需要调整了    
    //不在堆顶 并且 当前结点i的值比父结点小的时候继续向上调整 
    while(i!=1 && flag==0)
    {
        //判断是否比父结点的小 
        if (A[i]<A[i/2]) {
            swap(A, i, i/2);//交换和父节点的位置
            printf("\\n\\n第 %d 次调整堆：\\n", ++count);
            printHeap1(A);
        }
        else
            flag=1;//表示已经不需要调整了，当前结点的值比父结点的值要大 
        i=i/2; //更新编号i为它父结点的编号，从而便于下一次继续向上调整 
    }
}


int main(){
    int A[N+1] = { 0, 2, 7, 24, 11, 67, 35, 25, 16, 19, 97, 80, 50}; // 这里为了直接展示调整堆算法，直接给出已经建好堆的数组，免去建堆这一步，A[0]是不使用的，堆从A[1]开始。
    printf("初始化堆:\\n");
    printHeap(A);
    A[13] = 15; // 测试，堆尾增加值
    printf("\\n\\n堆尾增加一个15:\\n");
    printHeap1(A);
    goup(A, N, 13);
    return 0;
}

运行结果：

---

始于2009-05-26，西理工科协；更新至2016-06-02，杭州。