题目链接
题意:给一张无向图和\\(M\\)个询问,问\\(u,v\\)之间的路径的必经之点的个数。
对图建出圆方树,然后必经之点就是两点路径经过的原点个数,用\\((dep[u]+dep[v]-dep[LCA]*2)/2+1\\)即可算出。
什么你不知道圆方树(说的跟我知道一样)
\\(APIO2018\\)出来的黑科技,详见\\(APIO2018\\)铁人两项。
就是对每个点双新建一个点,然后让点双里所有点都对这个点连边。
看图。
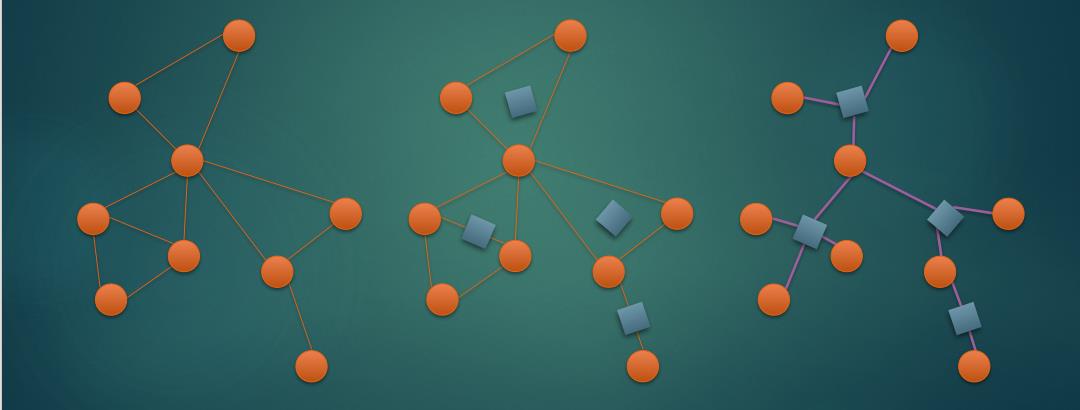
#include <cstdio>
const int MAXN = 500010;
const int MAXM = 1000010;
namespace IO{
int xjc; char ch;
inline int read(){
xjc = 0; ch = getchar();
while(ch < \'0\' || ch > \'9\') ch = getchar();
while(ch >= \'0\' && ch <= \'9\'){ xjc = xjc * 10 + ch - \'0\'; ch = getchar(); }
return xjc;
}
}using namespace IO;
inline int min(int a, int b){
return a > b ? b : a;
}
inline void swap(int &a, int &b){
xjc = a; a = b; b = xjc;
}
int n, m, k, a, b, cha;
struct Edge{
int next, to;
};
struct Graph{
int head[MAXN << 1], num;
Edge e[MAXM << 1];
inline void Add(int from, int to){
e[++num].to = to; e[num].next = head[from]; head[from] = num;
e[++num].to = from; e[num].next = head[to]; head[to] = num;
}
}G, T;
int dfn[MAXN], low[MAXN], vis[MAXN], stack[MAXN], f[MAXN << 1][20], dep[MAXN << 1], top, id, cnt;
void Tarjan(int u){
dfn[u] = low[u] = ++id; stack[++top] = u;
for(int i = G.head[u]; i; i = G.e[i].next)
if(!dfn[G.e[i].to]){
Tarjan(G.e[i].to);
low[u] = min(low[u], low[G.e[i].to]);
if(low[G.e[i].to] >= dfn[u]){
T.Add(u, ++cnt);
do T.Add(stack[top], cnt);
while(stack[top--] != G.e[i].to);
}
}
else low[u] = min(low[u], dfn[G.e[i].to]);
}
void getDF(int u, int fa){
f[u][0] = fa; dep[u] = dep[fa] + 1;
for(int i = T. head[u]; i; i = T.e[i].next)
if(T.e[i].to != fa)
getDF(T.e[i].to, u);
}
void make_ST(){
for(int j = 1; j <= 19; ++j)
for(int i = 1; i <= cnt; ++i)
f[i][j] = f[f[i][j - 1]][j - 1];
}
inline int LCA(int u, int v){
if(dep[u] < dep[v]) swap(u, v);
cha = dep[u] - dep[v];
if(cha)
for(int i = 0; i <= 19; ++i)
if(cha & (1 << i))
u = f[u][i];
if(u == v) return u;
for(int i = 19; ~i; --i)
if(f[u][i] != f[v][i])
u = f[u][i], v = f[v][i];
return f[u][0];
}
int main(){
cnt = n = read(); m = read();
for(int i = 1; i <= m; ++i)
G.Add(read(), read());
Tarjan(1);
getDF(1, 0);
make_ST();
k = read();
while(k--){
a = read(); b = read();
printf("%d\\n", ((dep[a] + dep[b] - (dep[LCA(a, b)] << 1)) >> 1) + 1);
}
return 0;
}