Opencv2.4.9源码分析——Random Trees
Posted zhaocj
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Opencv2.4.9源码分析——Random Trees相关的知识，希望对你有一定的参考价值。
一、原理
随机森林（Random Forest）的思想最早是由Ho于1995年首次提出，后来Breiman完整系统的发展了该算法，并命名为随机森林，而且他和他的博士学生兼同事Cutler把Random Forest注册成了商标，这可能也是Opencv把该算法命名为Random Trees的原因吧。
一片森林是由许多棵树木组成，森林中的每棵树可以说是彼此不相关，也就是说每棵树木的生长完全是由自身条件决定的，只有保持森林的多样性，森林才能更好的生长下去。随机森林算法与真实的森林相类似，它是由许多决策树组成，每棵决策树之间是不相关的。而随机森林算法的独特性就体现在“随机”这两个字上：通过随机抽取得到不同的样本来构建每棵决策树；决策树每个节点的最佳分叉属性是从由随机得到的特征属性集合中选取。下面就详细介绍这两次随机过程。
虽然在生成每棵决策树的时候，使用的是相同的参数，但使用的是不同的训练集合，这些训练集合是从全体训练样本中随机得到的，这一过程称之为bootstrap过程，得到的随机子集称之为bootstrap集合，而在bootstrap集合的基础上聚集得到的学习模型的过程称之为Bagging (Bootstrap aggregating)，那些不在bootstrap集合中的样本称之为OOB（Out Of Bag）。Bootstrap过程为：从全部N个样本中，有放回的随机抽取S次（在Opencv中，S=N），由于是有放回的抽取，所以肯定会出现同一个样本被抽取多次的现象，因此即使S=N，也会存在OOB。我们可以计算OOB样本所占比率：每个样本被抽取的概率为1/N，未被抽取的概率为(1－1/N)，抽取S次仍然没有被抽到的概率就为(1－1/N)S，如果S和N都趋于无穷大，则(1－1/N)S≈e－1＝0.368，即OOB样本所占全部样本约为36.8%，被抽取到的样本为63.2%。随机森林中的每棵决策树的bootstrap集合是不完全相同的，因此每棵决策树的OOB集合也是不完全相同的，所以对于训练集合中的某个样本来说，它可能属于决策树Ti的bootstrap集合，而属于决策树Tj的OOB集合。
因为在生成每棵决策树之前，都要进行bootstrap过程，而每次bootstrap过程所得到的bootstrap集合都会不同，所以保证了每棵决策树的不相关以及不相同。
为了进一步保证决策树的多样性，Breiman又提出了第二个随机性。一般的决策树是在全部特征属性中进行计算，从而得到最佳分叉属性，决策树的节点依据该属性进行分叉。而随机森林的决策树的最佳分叉属性是在一个特征属性随机子集内进行计算得到的。在全部p个特征属性中，随机选择q个特征属性，对于分类问题，q可以为p的平方根，对于回归问题，q可以为p的三分之一。对于随机森林中的所有决策树，随机子集内的特征属性的数量q是固定不变的，但不同的决策树，这q个特征属性是不同，而对于同一棵决策树，它的全部节点应用的是同一个随机子集。另外由于q远小于p，所以构建决策树时无需剪枝。
以上内容是在训练过程中，随机森林与其他基于决策树算法的不同之处。而在预测过程中，方法基本相同，预测样本作用于所有的决策树，对于分类问题，利用投票的方式，最多得票数的分类结果即为预测样本的分类，对于回归问题，所有决策树结果的平均值即为预测值。
再回到前面的训练过程中，为什么我们要使用Bagging方法？这是因为使用Bagging方法可以减小训练过程中的噪声和偏差，并且更重要的是，它还可以评估预测的误差和衡量特征属性的重要程度。
常用的评估机器学习算法的预测误差方法是交叉验证法，但该方法费时。而Bagging方法不需要交叉验证法，我们可以计算OOB误差，即利用那些36.8%的OOB样本来评估预测误差。已经得到证明，OOB误差是可以代替bootstrap集合误差的，并且其结果近似于交叉验证。OOB误差的另一个特点是它的计算是在训练的过程中同步得到的，即每得到一棵决策树，我们就可以根据该决策树来调整由前面的决策树得到的OOB误差。对于分类问题，它的OOB误差计算的方法和步骤为：
◆构建生成了决策树Tk，k=1, 2, …, K
①用Tk预测Tk的OOB样本的分类结果
②更新所有训练样本的OOB预测分类结果的次数（如样本xi是T1的OOB样本，则它有一个预测结果，而它是T2的bootstrap集合内的样本，则此时它没有预测结果）
③对所有样本，把每个样本的预测次数最多的分类作为该样本在Tk时的预测结果
④统计所有训练样本中预测错误的数量
⑤该数量除以Tk的OOB样本的数量作为Tk时的OOB误差
对于回归问题，它的OOB误差计算的方法和步骤为：
◆构建生成了决策树Tk，k=1, 2, …, K
①用Tk预测Tk的OOB样本的回归值
②累加所有训练样本中的OOB样本的预测值
③对所有样本，计算Tk时的每个样本的平均预测值，即预测累加值除以被预测的次数
④累加每个训练样本平均预测值与真实响应值之差的平方
⑤该平方累加和除以Tk的OOB样本的数量作为Tk时的OOB误差
很显然，随着决策树的增多，OOB误差会趋于缩小，因此我们可以设置一个精度ε，当Tk的OOB误差小于ε时，我们可以提前终止迭代过程，即不必再生成Tk+1及以后的决策树了。
不仅能够预测样本，而且还能够得到样本的哪个特征属性对预测起到决定作用，即特征属性的重要性，也是机器学习的一项主要任务，并且在实际应用中越来越重要。Bagging方法在随机森林中的另一个作用就是可以计算特征属性的重要程度。目前有两种主要的方法用于计算特征属性的重要性：Gini法和置换法。Gini法依据的是不纯度减小的原则，在这里我们重点介绍置换法。
置换法依据的原则是：样本的某个特征属性越重要，那么改变该特征属性的值，则该样本的预测值就越容易出现错误。置换法是通过置换两个样本的相同特征属性的值来改变特征属性的，它的具体方法是：在决策树Tk的OOB集合中随机选择两个样本xi=(xi,1,xi,2,…,xi,p)和xj=(xj,1,xj,2,…,xj,p)，每个样本具有p个特征属性，这两个样本的响应值分别为yi和yj，而用Tk对这两个样本的预测值分别为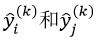
，设该OOB集合中一共有mk个样本。我们衡量第q个特征属性的重要性，则置换xi和xj中的xi,q和xj,q，置换后的样本为xi,jq=(xi,1,…,xj,q,…,xi,p)和xj,iq=(xj,1,…,xi,q,…,xj,p)。依据该方法，对OOB集合共置换mk次，则最终xi置换的结果为xi,πq=(xi,1,…,xπi,q,…,xi,p)。用Tk对xi,πq的预测值为
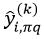。对于分类问题，如果
=yi，说明改变第q个特征属性的值，并不改变最终的响应值，也就是第q个特征属性对Tk来说不是很重要，而如果≠yi，说明改变第q个特征属性的值会改变最终的响应值，因此该特征属性重要。下式则为这种重要程度的量化形式：
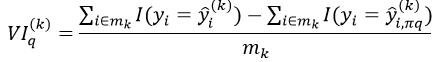（1）
式中，分子中的第一项表示对OOB中，预测正确的样本的数量，而分子中的第二项表示置换后预测正确的样本数量。而对于回归问题，它的重要程度的量化形式为：
（2）
式中，
（3）
如果第q个特征属性不属于Tk，VIq(k)＝0。对随机森林中的所有决策树都应用式1或式2计算第q个特征属性的重要性，则取平均得到整个随机森林对第q个特征属性的重要程度的量化形式为
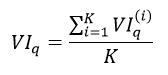（4）
最后，我们对所有的特征属性的重要程度进行归一化处理，则第q个特征属性的归一化为：
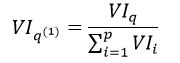（5）
至从随机森林提出以来，该算法已成为一种流行的被广泛使用的非参数回归应用的工具。Breiman对该算法总结了以下一些特点：
●在目前所有的机器学习算法中，具有无法比拟的预测精度
●能够有效的处理大型数据库
●不需要任何的特征属性的删减，就能够处理具有上千种特征属性的样本
●能够给出特征属性的重要程度
●在随机森林的构建过程中，就可以得到泛化误差的内部无偏估计
●即使包含一定比例的缺失特征属性的样本，也能够得到准确的预测
●在样本种群不均衡的数据库中，也能够平衡这种情况
●构建好的随机森林可以被保存下来，用于以后的其他数据的使用
二、源码分析
我们先给出表示随机森林参数的类的一个构造函数：
CvRTParams::CvRTParams( int _max_depth, int _min_sample_count,
float _regression_accuracy, bool _use_surrogates,
int _max_categories, const float* _priors, bool _calc_var_importance,
int _nactive_vars, int max_num_of_trees_in_the_forest,
float forest_accuracy, int termcrit_type ) :
CvDTreeParams( _max_depth, _min_sample_count, _regression_accuracy,
_use_surrogates, _max_categories, 0,
false, false, _priors ),
calc_var_importance(_calc_var_importance),
nactive_vars(_nactive_vars)
{
term_crit = cvTermCriteria(termcrit_type,
max_num_of_trees_in_the_forest, forest_accuracy);
}
_max_depth表示决策树的深度，该值的大小严重影响拟合的效果
_min_sample_count表示决策树节点的最小样本数，如果节点的样本数小于该值，则该节点不再分叉，一般该值为样本总数的1%
_regression_accuracy表示终止构建回归树的一个条件，回归树的响应值的精度如果达到了该值，则无需再分叉。该值不能小于0，否则报错
_use_surrogates表示是否使用替代分叉节点
_max_categories表示特征属性为类的形式的最大的类的数量
_priors表示决策树的特征属性的先验概率
以上几个参数是用于构建决策树时的参数CvDTreeParams，其中0表示不使用交叉验证方法，两个false分别表示不应用1SE规则和不移除被剪掉的节点。
_calc_var_importance表示是否计算特征属性的重要程度
_nactive_vars表示用于寻找最佳分叉属性的每个节点的随机特征属性的数量，如果该值设置为0，则表示该值为样本的全部特征属性的平方根
max_num_of_trees_in_the_forest表示森林中决策树的最大数量，也就是最大迭代次数，因为每迭代一次就会得到一棵决策树。通常来说，决策树越多，预测越准确，但决策树的数量达到一定程度后，准确度的增长会减小甚至趋于不变，另一方面，预测时间是与决策树的数量呈线性关系的
forest_accuracy表示OOB误差的精度要求
termcrit_type表示随机森林构建的终止准则，CV_TERMCRIT_ITER以决策树达到max_num_of_trees_in_the_forest为终止条件；CV_TERMCRIT_EPS以精度到达forest_accuracy为终止条件；CV_TERMCRIT_ITER | CV_TERMCRIT_EPS为任一条件达到即终止
缺省的CvRTParams构造函数为：
CvRTParams::CvRTParams() : CvDTreeParams( 5, 10, 0, false, 10, 0, false, false, 0 ),
calc_var_importance(false), nactive_vars(0)
{
term_crit = cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 50, 0.1 );
}
CvRTrees::CvRTrees()
{
nclasses = 0; //表示分类类别数量
oob_error = 0; //表示OOB误差
ntrees = 0; //表示决策树的数量
trees = NULL; //表示决策树
data = NULL; //表示用于构建决策树的样本数据
active_var_mask = NULL; //表示随机特征属性的掩码
var_importance = NULL; //表示特征属性的重要性
rng = &cv::theRNG(); //实例化rng，表示随机数
default_model_name = "my_random_trees";
}
bool CvRTrees::train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx,
const CvMat* _sample_idx, const CvMat* _var_type,
const CvMat* _missing_mask, CvRTParams params )
//_train_data训练样本数据，必须为32FC1类型的矩阵形式
//_tflag训练数据的特征属性类型，如果为CV_ROW_SAMPLE，表示样本是以行的形式储存的，即_train_data矩阵的每一行为一个样本；如果为CV_COL_SAMPLE，表示样本是以列的形式储存的
//_responses样本的结果，即响应值，该值必须是32SC1或32FC1类型的一维矩阵（即矢量）的形式，并且元素的数量必须与训练样本数据_train_data的样本数一致
//_var_idx标识感兴趣的特征属性，即真正用于训练的那些特征属性，该值的形式与_sample_idx变量相似
//_sample_idx标识感兴趣的样本，即真正用于训练的样本，该值必须是一维矩阵的形式，即矢量的形式，并且类型必须是8UC1、8SU1或者32SC1。如果为8UC1或8SU1，则该值的含义是用掩码的形式表示对应的样本，即0表示不感兴趣的样本，其他数为感兴趣的样本，因此矢量的元素数量必须与训练样本数据_train_data的样本数一致；如果为32SC1，则该值的含义是那些感兴趣的样本的索引，而不感兴趣的样本的索引不在该矢量中出现，因此该矢量的元素数量可以小于或等于_train_data的样本数
//_var_type特征属性的形式，是类的形式还是数值的形式，用掩码的形式表现对应特征属性的形式，0表示为数值的形式，1表示为类的形式。该值必须是一维矩阵，并且元素的数量必须是真正用于训练的那些特征属性的数量加1，多余的一个元素表示的是响应值的形式，即是分类树还是回归树
//_missing_mask缺失的特征属性，用掩码的形式表现对应的特征属性，0表示没有缺失，而且必须与_train_data的矩阵尺寸大小一致
//params为构建随机森林的参数
{
clear(); //清空一些全局变量
//得到用于构建决策树的参数
CvDTreeParams tree_params( params.max_depth, params.min_sample_count,
params.regression_accuracy, params.use_surrogates, params.max_categories,
params.cv_folds, params.use_1se_rule, false, params.priors );
data = new CvDTreeTrainData(); //实例化data
//得到用于构建决策树的样本数据
data->set_data( _train_data, _tflag, _responses, _var_idx,
_sample_idx, _var_type, _missing_mask, tree_params, true);
int var_count = data->var_count; //表示特征属性的数量
//随机特征属性的数量nactive_vars一定不能大于全部特征属性的数量var_count
if( params.nactive_vars > var_count )
params.nactive_vars = var_count;
//如果nactive_vars为0，则nactive_vars重新赋值为var_count的平方根
else if( params.nactive_vars == 0 )
params.nactive_vars = (int)sqrt((double)var_count);
else if( params.nactive_vars < 0 ) //如果nactive_vars小于0，则报错
CV_Error( CV_StsBadArg, "<nactive_vars> must be non-negative" );
// Create mask of active variables at the tree nodes
//创建一个用于特征属性掩码的变量
active_var_mask = cvCreateMat( 1, var_count, CV_8UC1 );
//如果calc_var_importance为true，则创建一个用于表示特征属性重要性的变量
if( params.calc_var_importance )
{
var_importance = cvCreateMat( 1, var_count, CV_32FC1 );
cvZero(var_importance); //初始化为0
}
{ // initialize active variables mask
CvMat submask1, submask2;
//确保全部特征属性的数量不能小于1，随机特征属性的数量不能小于0，并且前者不能小于后者
CV_Assert( (active_var_mask->cols >= 1) && (params.nactive_vars > 0) && (params.nactive_vars <= active_var_mask->cols) );
//对于active_var_mask矩阵，前nactive_vars列的所有元素赋值为1，其余的赋值为0
cvGetCols( active_var_mask, &submask1, 0, params.nactive_vars );
cvSet( &submask1, cvScalar(1) );
if( params.nactive_vars < active_var_mask->cols )
{
cvGetCols( active_var_mask, &submask2, params.nactive_vars, var_count );
cvZero( &submask2 );
}
}
//调用grow_forest函数，由决策树构建森林
return grow_forest( params.term_crit );
}
bool CvRTrees::grow_forest( const CvTermCriteria term_crit )
{
//表示用于构建单棵决策树的随机样本的掩码，抽取到的样本掩码为0xFF，否则为0
CvMat* sample_idx_mask_for_tree = 0;
//表示用于构建单棵决策树的随机样本，该矩阵存储的是这些样本在全部样本中的索引值
CvMat* sample_idx_for_tree = 0;
const int max_ntrees = term_crit.max_iter; //得到最大迭代次数
const double max_oob_err = term_crit.epsilon; //得到OOB误差精度
const int dims = data->var_count; //得到样本的特征属性的数量
float maximal_response = 0; //表示最大的响应值，即式3中的参数A
//表示OOB样本的响应值的投票结果，用于分类问题
CvMat* oob_sample_votes = 0;
CvMat* oob_responses = 0; //OOB样本的响应值，用于回归问题
float* oob_samples_perm_ptr= 0; //OOB样本的置换指针
float* samples_ptr = 0; //表示样本矩阵的首地址指针
uchar* missing_ptr = 0; //表示缺失特征属性矩阵的首地址指针
float* true_resp_ptr = 0; //表示样本响应值矩阵的首地址指针
//该标识变量表示应用OOB误差精度或需要计算特征属性重要程度
bool is_oob_or_vimportance = (max_oob_err > 0 && term_crit.type != CV_TERMCRIT_ITER) || var_importance;
// oob_predictions_sum[i] = sum of predicted values for the i-th sample
// oob_num_of_predictions[i] = number of summands
// (number of predictions for the i-th sample)
// initialize these variable to avoid warning C4701
// oob_predictions_sum表示某个训练样本在所有决策树OOB集合中的预测值累加和
CvMat oob_predictions_sum = cvMat( 1, 1, CV_32FC1 );
// oob_num_of_predictions表示某个训练样本在所有决策树OOB集合中的被预测数量
CvMat oob_num_of_predictions = cvMat( 1, 1, CV_32FC1 );
nsamples = data->sample_count; //表示样本的全体数量
nclasses = data->get_num_classes(); //表示分类问题的样本分类类别数量
if ( is_oob_or_vimportance ) //该变量为真
{
if( data->is_classifier ) //分类问题
{
//创建oob_sample_votes变量，矩阵大小为样本总数×分类类别数
oob_sample_votes = cvCreateMat( nsamples, nclasses, CV_32SC1 );
cvZero(oob_sample_votes); //初始化为0
}
else //回归问题
{
// oob_responses[0,i] = oob_predictions_sum[i]
// = sum of predicted values for the i-th sample
// oob_responses[1,i] = oob_num_of_predictions[i]
// = number of summands (number of predictions for the i-th sample)
//创建oob_responses变量，矩阵大小为2×样本总数，其中oob_responses[0,i] = oob_predictions_sum[i]，oob_responses[1,i] = oob_num_of_predictions[i]
oob_responses = cvCreateMat( 2, nsamples, CV_32FC1 );
cvZero(oob_responses); //初始化为0
// oob_predictions_sum指向矩阵oob_responses的第0行
cvGetRow( oob_responses, &oob_predictions_sum, 0 );
// oob_num_of_predictions指向矩阵oob_responses的第1行
cvGetRow( oob_responses, &oob_num_of_predictions, 1 );
}
//分配空间给下面4个变量
oob_samples_perm_ptr = (float*)cvAlloc( sizeof(float)*nsamples*dims );
samples_ptr = (float*)cvAlloc( sizeof(float)*nsamples*dims );
missing_ptr = (uchar*)cvAlloc( sizeof(uchar)*nsamples*dims );
true_resp_ptr = (float*)cvAlloc( sizeof(float)*nsamples );
//从样本数据中得到指针samples_ptr、missing_ptr和true_resp_ptr
data->get_vectors( 0, samples_ptr, missing_ptr, true_resp_ptr );
double minval, maxval;
//定义并得到样本的响应值
CvMat responses = cvMat(1, nsamples, CV_32FC1, true_resp_ptr);
//得到响应值中的最大值maxval和最小值minval，minval有可能是负数
cvMinMaxLoc( &responses, &minval, &maxval );
//式3
maximal_response = (float)MAX( MAX( fabs(minval), fabs(maxval) ), 0 );
}
//为trees分配内存空间
trees = (CvForestTree**)cvAlloc( sizeof(trees[0])*max_ntrees );
memset( trees, 0, sizeof(trees[0])*max_ntrees ); //决策树trees初始化为0
//创建下面两个变量
sample_idx_mask_for_tree = cvCreateMat( 1, nsamples, CV_8UC1 );
sample_idx_for_tree = cvCreateMat( 1, nsamples, CV_32SC1 );
ntrees = 0; //决策树的索引值，先初始化为0
//进入构建随机森林的循环体中
while( ntrees < max_ntrees ) //满足最大迭代次数时，结束迭代
{
// oob_samples_count用于OOB样本计数
int i, oob_samples_count = 0;
//分类问题，该值表示式1中分子的第一项；回归问题，为式2中的分子第一项
double ncorrect_responses = 0; // used for estimation of variable importance
CvForestTree* tree = 0; //实例化CvForestTree类，表示当前要构建的决策树
cvZero( sample_idx_mask_for_tree ); //初始化0
//遍历所有样本，得到用于构建决策树的样本
for(i = 0; i < nsamples; i++ ) //form sample for creation one tree
{
//在全体样本中，有放回的随机抽取一个样本，一共抽取nsamples次
//idx为一个不大于nsamples的随机整数，该语句的含义是随机抽取某个样本，idx表示该样本的索引值
int idx = (*rng)(nsamples);
sample_idx_for_tree->data.i[i] = idx; //赋值样本的索引值
sample_idx_mask_for_tree->data.ptr[idx] = 0xFF; //该样本的掩码
}
trees[ntrees] = new CvForestTree(); //实例化随机森林
tree = trees[ntrees]; //决策树赋值
//训练单棵决策树，它首先调用CvForestTree类中的train虚函数，而最终调用的是CvDTree类的do_train函数，该函数的详细讲解请看我的关于决策树那篇文章。但这里在执行do_train函数时，会调用CvForestTree类中的find_best_split函数，该函数在后面给此详细的介绍
tree->train( data, sample_idx_for_tree, this );
if ( is_oob_or_vimportance ) //如果该变量为true
{
// sample表示当前样本，missing表示缺失的特征属性
CvMat sample, missing;
// form array of OOB samples indices and get these samples
sample = cvMat( 1, dims, CV_32FC1, samples_ptr );
missing = cvMat( 1, dims, CV_8UC1, missing_ptr );
oob_error = 0; //初始化为0
for( i = 0; i < nsamples; i++,
sample.data.fl += dims, missing.data.ptr += dims ) //遍历所有样本
{
CvDTreeNode* predicted_node = 0; //表示预测结果的叶节点
// check if the sample is OOB
//判断当前的样本是否用于构建当前决策树，如果是则遍历下一个样本
if( sample_idx_mask_for_tree->data.ptr[i] )
continue;
// predict oob samples
//得到当前OOB样本的预测结果的叶节点
if( !predicted_node )
predicted_node = tree->predict(&sample, &missing, true);
if( !data->is_classifier ) //regression回归问题
{
//resp为当前样本的预测值，avg_resp为响应值的平均值
double avg_resp, resp = predicted_node->value;
// OOB误差步骤的第②步，第i个样本的预测值的累加和
oob_predictions_sum.data.fl[i] += (float)resp;
oob_num_of_predictions.data.fl[i] += 1; //第i个样本被预测的次数
// compute oob error
// OOB误差步骤的第③步，计算平均预测值
avg_resp = oob_predictions_sum.data.fl[i]/oob_num_of_predictions.data.fl[i];
//样本平均预测值与真实响应值之差
avg_resp -= true_resp_ptr[i];
// OOB误差步骤的第④步
oob_error += avg_resp*avg_resp;
//式2中分子第一项中的e的指数部分
resp = (resp - true_resp_ptr[i])/maximal_response;
//式2中分子第一项内容
ncorrect_responses += exp( -resp*resp );
}
else //classification分类问题
{
double prdct_resp; //表示预测结果
CvPoint max_loc; //表示最多得票值的位置
CvMat votes; //表示投票结果
//votes为oob_sample_votes矩阵的第i行，即当前样本的分类
cvGetRow(oob_sample_votes, &votes, i);
//OOB误差步骤的第②步，统计OOB预测分类结果的次数
votes.data.i[predicted_node->class_idx]++;
// compute oob error
// max_loc表示当前样本预测次数最多的分类的位置
cvMinMaxLoc( &votes, 0, 0, 0, &max_loc );
//得到当前样本预测分类结果的映射值，OOB误差步骤的第③步
prdct_resp = data->cat_map->data.i[max_loc.x];
// OOB误差步骤的第④步，统计预测错误的数量
oob_error += (fabs(prdct_resp - true_resp_ptr[i]) < FLT_EPSILON) ? 0 : 1;
//统计当前决策树的OOB样本预测正确的样本数，式1中分子的第一项内容
ncorrect_responses += cvRound(predicted_node->value - true_resp_ptr[i]) == 0;
}
oob_samples_count++; //OOB样本计数
} //遍历所有样本结束
// OOB误差步骤的第⑤步
if( oob_samples_count > 0 )
oob_error /= (double)oob_samples_count;
// estimate variable importance
//评估特征属性的重要程度
if( var_importance && oob_samples_count > 0 )
{
int m; //用于特征属性的循环索引
//赋值样本数据samples_ptr给oob_samples_perm_ptr
memcpy( oob_samples_perm_ptr, samples_ptr, dims*nsamples*sizeof(float));
for( m = 0; m < dims; m++ ) //遍历所有的特征属性
{
//该值表示式1或式2中分子的第二项内容
double ncorrect_responses_permuted = 0;
// randomly permute values of the m-th variable in the oob samples
//指向第m个特征属性
float* mth_var_ptr = oob_samples_perm_ptr + m;
//所有OOB样本的第m个特征属性都要随机置换
for( i = 0; i < nsamples; i++ ) //遍历所有样本
{
int i1, i2;
float temp;
//当前样本不是OOB，则继续遍历下个样本
if( sample_idx_mask_for_tree->data.ptr[i] ) //the sample is not OOB
continue;
//在全体样本中，随机得到两个样本i1和i2
i1 = (*rng)(nsamples);
i2 = (*rng)(nsamples);
//置换这两个样本在第m个特征属性的值
CV_SWAP( mth_var_ptr[i1*dims], mth_var_ptr[i2*dims], temp );
// turn values of (m-1)-th variable, that were permuted
// at the previous iteration, untouched
//下面语句的作用是保持第m-1个特征属性（上一次的迭代）不置换，也就是每次只置换一个特征属性
if( m > 1 )
oob_samples_perm_ptr[i*dims+m-1] = samples_ptr[i*dims+m-1];
}
// predict "permuted" cases and calculate the number of votes for the
// correct class in the variable-m-permuted oob data
//重新赋值置换以后的样本
sample = cvMat( 1, dims, CV_32FC1, oob_samples_perm_ptr );
missing = cvMat( 1, dims, CV_8UC1, missing_ptr );
for( i = 0; i < nsamples; i++, //遍历所有样本
sample.data.fl += dims, missing.data.ptr += dims )
{
double predct_resp, true_resp;
//当前样本不是OOB，则继续遍历下个样本
if( sample_idx_mask_for_tree->data.ptr[i] ) //the sample is not OOB
continue;
//得到当前置换后样本的预测值
predct_resp = tree->predict(&sample, &missing, true)->value;
true_resp = true_resp_ptr[i]; //置换前样本的响应值
if( data->is_classifier ) //分类问题
//统计置换后预测正确的样本数量，式1分子的第二项内容
ncorrect_responses_permuted += cvRound(true_resp - predct_resp) == 0;
else //回归问题
{
//式2分子的第二项中e的指数部分
true_resp = (true_resp - predct_resp)/maximal_response;
//式2分子的第二项内容
ncorrect_responses_permuted += exp( -true_resp*true_resp );
}
}
//式1或式2，以及式4，因为后面要进行归一化，所以无需除法
var_importance->data.fl[m] += (float)(ncorrect_responses
- ncorrect_responses_permuted);
}
}
}
ntrees++; //迭代次数加1，即决策树的数量加1
//如果满足OOB误差的精度要求，则提前退出迭代，即结束while循环
if( term_crit.type != CV_TERMCRIT_ITER && oob_error < max_oob_err )
break;
} //while循环结束
//归一化var_importance，即归一化各个特征属性的重要性程度
if( var_importance )
{
for ( int vi = 0; vi < var_importance->cols; vi++ )
var_importance->data.fl[vi] = ( var_importance->data.fl[vi] > 0 ) ?
var_importance->data.fl[vi] : 0;
cvNormalize( var_importance, var_importance, 1., 0, CV_L1 );
}
//清空一些变量
cvFree( &oob_samples_perm_ptr );
cvFree( &samples_ptr );
cvFree( &missing_ptr );
cvFree( &true_resp_ptr );
cvReleaseMat( &sample_idx_mask_for_tree );
cvReleaseMat( &sample_idx_for_tree );
cvReleaseMat( &oob_sample_votes );
cvReleaseMat( &oob_responses );
return true;
}
CvDTreeSplit* CvForestTree::find_best_split( CvDTreeNode* node )
{
CvMat* active_var_mask = 0; //表示随机特征属性的掩码
if( forest ) //已构建了随机森林
{
int var_count; //全部特征属性的数量
//得到随机数的分布类型，是均匀分布（UNIFORM）还是高斯正态分布（NORMAL）
CvRNG* rng = forest->get_rng();
active_var_mask = forest->get_active_var_mask(); //得到随机特征属性的掩码
var_count = active_var_mask->cols; //得到全部特征属性的数量
CV_Assert( var_count == data->var_count ); //确保var_count的正确
//遍历所有的特征属性，随机得到nactive_vars个特征属性，在active_var_mask向量中，前nactive_vars项为1，其余为0，下面的语句通过随机调整向量元素的位置，实现了打乱那些值为1的元素的位置，从而达到了随机得到nactive_vars个特征属性的目的
for( int vi = 0; vi < var_count; vi++ )
{
uchar temp;
//随机得到两个不大于var_count的值，用于表示随机得到的特征属性
int i1 = cvRandInt(rng) % var_count;
int i2 = cvRandInt(rng) % var_count;
//交换这两个特征属性的位置
CV_SWAP( active_var_mask->data.ptr[i1],
active_var_mask->data.ptr[i2], temp );
}
}
//实例化ForestTreeBestSplitFinder类
cv::ForestTreeBestSplitFinder finder( this, node );
//并行处理，调用ForestTreeBestSplitFinder类的重载( )运算符，见后面的介绍
cv::parallel_reduce(cv::BlockedRange(0, data->var_count), finder);
CvDTreeSplit *bestSplit = 0; //表示最佳分叉属性
if( finder.bestSplit->quality > 0 ) //得到了最佳分叉属性
{
bestSplit = data->new_split_cat( 0, -1.0f );
memcpy( bestSplit, finder.bestSplit, finder.splitSize );
}
return bestSplit; //返回最佳分叉属性
}
void ForestTreeBestSplitFinder::operator()(const BlockedRange& range)
{
int vi, vi1 = range.begin(), vi2 = range.end(); //作用范围为全部特征属性
int n = node->sample_count; //该节点的样本数量
CvDTreeTrainData* data = tree->get_data(); //得到样本数据
AutoBuffer<uchar> inn_buf(2*n*(sizeof(int) + sizeof(float))); //开辟内存空间
CvForestTree* ftree = (CvForestTree*)tree; //实例化CvForestTree类
//得到随机特征属性的掩码
const CvMat* active_var_mask = ftree->forest->get_active_var_mask();
for( vi = vi1; vi < vi2; vi++ ) //遍历所有特征属性
{
CvDTreeSplit *res; //表示分叉属性
int ci = data->var_type->data.i[vi]; //得到当前特征属性的值
//如果该节点不具有当前特征属性，或当前特征属性不在随机得到的特征属性集合中，则继续下一个特征属性的遍历
if( node->num_valid[vi] <= 1
|| (active_var_mask && !active_var_mask->data.ptr[vi]) )
continue;
if( data->is_classifier ) //分类问题
{
if( ci >= 0 ) //当前特征属性为类别型特征属性
res = ftree->find_split_cat_class( node, vi, bestSplit->quality, split, (uchar*)inn_buf ); //找到最佳分叉属性
else //当前特征属性为数值型特征属性
res = ftree->find_split_ord_class( node, vi, bestSplit->quality, split, (uchar*)inn_buf ); //找到最佳分叉属性
}
else //回归问题
{
if( ci >= 0 ) //当前特征属性为类别型特征属性
res = ftree->find_split_cat_reg( node, vi, bestSplit->quality, split, (uchar*)inn_buf ); //找到最佳分叉属性
else //当前特征属性为数值型特征属性
res = ftree->find_split_ord_reg( node, vi, bestSplit->quality, split, (uchar*)inn_buf ); //找到最佳分叉属性
}
//得到了最佳分叉属性bestSplit
if( res && bestSplit->quality < split->quality )
memcpy( (CvDTreeSplit*)bestSplit, (CvDTreeSplit*)split, splitSize );
}
}
float CvRTrees::predict( const CvMat* sample, const CvMat* missing ) const
{
double result = -1; //表示预测结果，该函数的返回值
int k;
if( nclasses > 0 ) //classification 分类问题
{
int max_nvotes = 0; //表示最多投票数
cv::AutoBuffer<int> _votes(nclasses); //分配空间
int* votes = _votes; //赋值
memset( votes, 0, sizeof(*votes)*nclasses ); //初始化votes，清零
for( k = 0; k < ntrees; k++ ) //遍历森林中的所有决策树
{
//得到预测样本的预测叶节点
CvDTreeNode* predicted_node = trees[k]->predict( sample, missing );
int nvotes; //表示得票数
int class_idx = predicted_node->class_idx; //表示分类的索引值
CV_Assert( 0 <= class_idx && class_idx < nclasses ); //确保索引值正确
nvotes = ++votes[class_idx]; //统计得票数
if( nvotes > max_nvotes ) //更新最多投票数
{
max_nvotes = nvotes; //最多投票数
result = predicted_node->value; //最多投票数的分类为最终预测结果
}
}
}
else // regression 回归问题
{
result = 0;
for( k = 0; k < ntrees; k++ ) //遍历森林中的所有决策树
result += trees[k]->predict( sample, missing )->value; //累加预测结果
result /= (double)ntrees; //取平均值
}
return (float)result; //返回预测结果
}
三、应用实例
我们仍然应用上一篇文章中给出的房屋售价的实例，对房屋面积为201.5，房间数量为3的房屋进行预测售价：
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/ml/ml.hpp"
#include <iostream>
using namespace cv;
using namespace std;
int main( int argc, char** argv )
{
double trainingData[28][2]={{210.4, 3}, {240.0, 3}, {300.0, 4}, {153.4, 3}, {138.0, 3},
{194.0,4}, {189.0, 3}, {126.8, 3}, {132.0, 2}, {260.9, 4},
{176.7,3}, {160.4, 3}, {389.0, 3}, {145.8, 3}, {160.0, 3},
{141.6,2}, {198.5, 4}, {142.7, 3}, {149.4, 3}, {200.0, 3},
{447.8,5}, {230.0, 4}, {123.6, 3}, {303.1, 4}, {188.8, 2},
{196.2,4}, {110.0, 3}, {252.6, 3} };
CvMat trainingDataCvMat = cvMat( 28, 2, CV_32FC1, trainingData );
float responses[28] = { 399900, 369000, 539900, 314900, 212000, 239999, 329999,
259900, 299900, 499998, 252900, 242900, 573900, 464500,
329900, 232000, 299900, 198999, 242500, 347000, 699900,
449900, 199900, 599000, 255000, 259900, 249900, 469000};
CvMat responsesCvMat = cvMat( 28, 1, CV_32FC1, responses );
CvRTParams params= CvRTParams(10, 2, 0, false,16, 0, true, 0, 100, 0, CV_TERMCRIT_ITER );
CvRTrees rtrees;
rtrees.train(&trainingDataCvMat, CV_ROW_SAMPLE, &responsesCvMat,
NULL, NULL, NULL, NULL,params);
double sampleData[2]={201.5, 3};
Mat sampleMat(2, 1, CV_32FC1, sampleData);
float r = rtrees.predict(sampleMat);
cout<<endl<<"result: "<<r<<endl;
return 0;
}
最终的输出值为：
result: 252900以上是关于Opencv2.4.9源码分析——Random Trees的主要内容，如果未能解决你的问题，请参考以下文章
Opencv2.4.9源码分析——Gradient Boosted Trees
Win7下qt5.3.1+opencv2.4.9编译环境的搭建（好多 Opencv2.4.9源码分析的博客）