机器学习--- SVM的学习：理论基础理解

Posted 我只是一个单纯的2

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习--- SVM的学习：理论基础理解相关的知识，希望对你有一定的参考价值。

SVM是一种应用比较广泛的分类器，全名为Support Vector Machine，即支持向量机，在没有学习SVM之前，我对这个分类器汉字的理解是支持/向量机，学习之后，才知道原名是支持向量/机，我对这个分类器的名字理解是：通过具有稀疏性质的一系列支持向量从而得到一个比较好的分类器，这个分类器在名称里面体现为Machine。下面是我对于学习SVM理论后认为几个需要理解和掌握的知识点

  • 函数间隔(functional margin) and 几何间隔(geometric margin)
  • 支持向量的理解
  • SVM的最优化问题的解决
首先给出一个一般介绍SVM开篇的一类型的图：

从这幅图上看，可以很清楚的看见，SVM实现了两类数据的分类，在这幅图中，有中间的一条横线就是我们要得到的分类器，在二维平面表现为直线(线性分类)或者曲线(非线性分类)，在高维空间表现为超平面(hyperplane)。

回顾一下机器学习（一）--- 监督学习之回归中有关于逻辑回归的知识：对于分类器hypothesis，，在而进行二分类的问题上,现在对于该函数，用超平面的表达式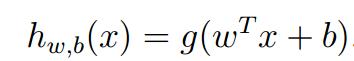：进行替换，对于二分类问题而言，需要说明的是：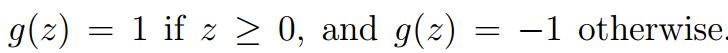

联系该公式与上图之间的联系，当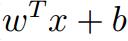大于0的时候，则数据分类的label为1，反之则定为-1。由此引出关于函数间隔的定义，functional margin:

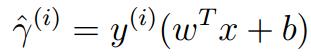
其中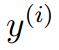，的值为{+1,-1}，当值为+1时，为了达到很好的分类效果，括号里面的值需要表现为positive，且是较为大的正值，而对值为-1，括号里面的值则需要表现为negative,且是绝对值较为大的负值。

为了比较大的函数间隔，达到很好的confidence，即分类结果更加准确可信，有可能简单的增加w和b的值，但是这样简单的处理是没有任何意义的，因为我们的目的就是为了找到一个比较好的超平面，应该是w,b是不同，在三维空间内，w代表的是分类平面的法向量，对于简单的乘上一个因子，实质上平面并没有发生改变，因此这并不是我们需要的结果。

接着我们需要引出几何间隔，geometric margin的概念。

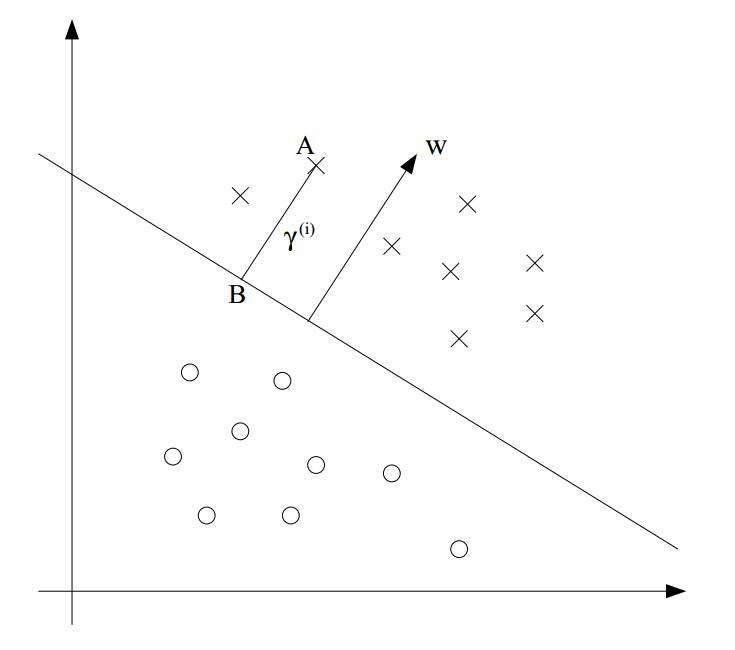
对于上图，B点是A点在超平面上的投影，对于B点的坐标，这是一个很简单的立体几何问题，对于超平面的法向量，w，我们可以很容易求得它的单位向量，由此可以余弦角，由此可以很容易根据A的坐标求得B的坐标，即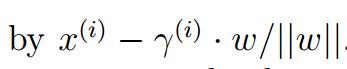：。由因为B点是落在超平面上的，由此可以得到以下结果：

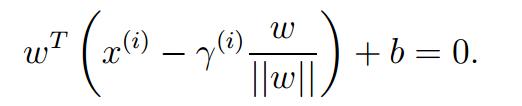
经过简单的线性代数的处理，可以得到：

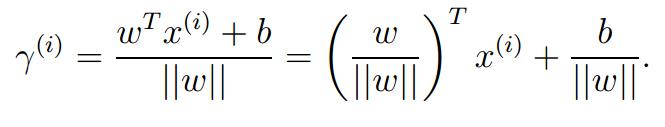
感觉是不是有点似曾显示的感觉，非常类似点到平面的距离的公式，因为它有可能是负值，因为少了一个绝对值符号，再经过简单的处理：

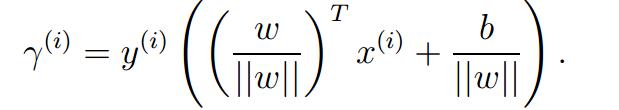
这样就保证了非负性质。这就是几何间隔的定义式。

可以看到几何间隔和函数间隔是非常类似的，但是点到平面的距离是不会因为w,b的缩发生变化，在这一点上，几何间隔比函数间隔更具有意义和价值。

因此，对于以上的二分类问题，可以得到以下的抽象模型：定义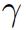

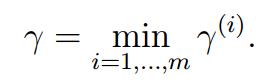
即：通过学习和训练，可以得到一组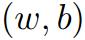,使得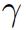能够达到最大。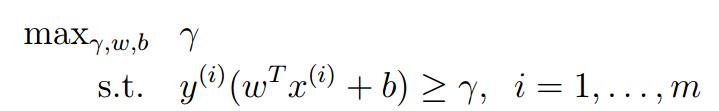


===================================================================================

接下来需要讨论上面提出的模型的求解问题。

通过函数间隔和几何间隔的关系，经过转换，可以得到：

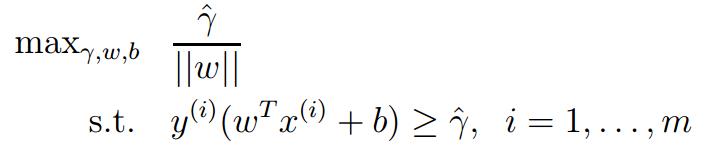
这里需要深入的讨论一下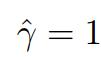的问题。这也是我在理解SVM的时候始终不太明白的问题，在SVM的理论学习中，通常会有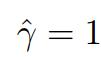。的限制