BZOJ_1005_ [HNOI2008]_明明的烦恼_(组合数学+purfer_sequence+高精度+分解因数)
Posted 晴歌。
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BZOJ_1005_ [HNOI2008]_明明的烦恼_(组合数学+purfer_sequence+高精度+分解因数)相关的知识,希望对你有一定的参考价值。
描述
http://www.lydsy.com/JudgeOnline/problem.php?id=1005
一棵树有n个点,给出没给节点的度,如果没有限制则为-1,求共有多少种可能的树.
分析
蒟蒻我肯定是不会做的,所以先来抄一段题解...
这题需要了解一种数列: Purfer Sequence
我们知道,一棵树可以用括号序列来表示,但是,一棵顶点标号(1~n)的树,还可以用一个叫做 Purfer Sequence 的数列表示
一个含有 n 个节点的 Purfer Sequence 有 n-2 个数,Purfer Sequence 中的每个数是 1~n 中的一个数
一个定理:一个 Purfer Sequence 和一棵树一一对应
先看看怎么由一个树得到 Purfer Sequence
由 一棵树得到它的 Purfer Sequence 总共需要 n-2 步,每一步都在当前的树中寻找具有最小标号的叶子节点(度为 1),将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素,并将此叶子节点从树中删除,直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树
看看下面的例子:
假设有一颗树有 5 个节点,四条边依次为:(1, 2), (1, 3), (2, 4), (2, 5),如下图所示:

第 1 步,选取具有最小标号的叶子节点 3,将与它相连的点 1 作为第 1 个 Purfer Number,并从树中删掉节点 3:
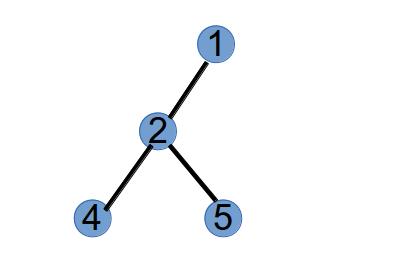
第 2 步,选取最小标号的叶子节点 1,将与其相连的点 2 作为第 2 个 Purfer Number,并从树中删掉点 1:
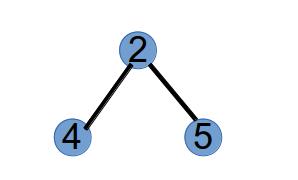
第 3 步,选取最小标号的叶子节点 4,将与其相连的点 2 作为第 3 个 Purfer Number,并从树中删掉点 4:
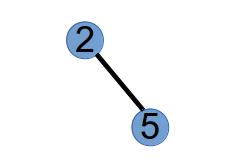
最后,我们得到的 Purfer Sequence 为:1 2 2
不难看出,上面的步骤得到的 Purfer Sequence 具有唯一性,也就是说,一个树,只能得到一个唯一的 Purfer Sequence
接下来看,怎么由一个 Purfer Sequence 得到一个树
由 Purfer Sequence 得到一棵树,先将所有编号为 1 到 n 的点的度赋初值为 1,然后加上它在 Purfer Sequence 中出现的次数,得到每个点的度
先执行 n-2 步,每一步,选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连,得到树中的一条边,并将 u 和 v 的度减一
最后再把剩下的两个度为 1 的点连边,加入到树中
我们可以根据上面的例子得到的 Purfer Sequence :1 2 2 重新得到一棵树
Purfer Sequence 中共有 3 个数,可以知道,它表示的树中共有 5 个点,按照上面的方法计算他们的度为下表所示:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 2 | 3 | 1 | 1 | 1 |
第 1 次执行,选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边:
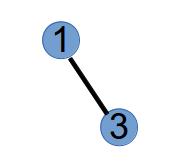
将 1 和 3 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 1 | 3 | 0 | 1 | 1 |
第 2 次执行,选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边:
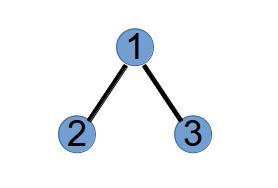
将 1 和 2 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 2 | 0 | 1 | 1 |
第 3 次执行,将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边:
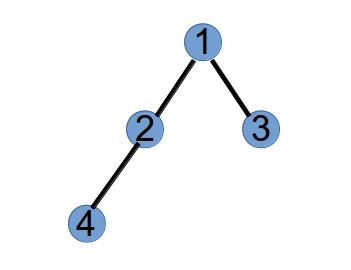
将 2 和 4 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 1 | 0 | 0 | 1 |
最后,还剩下两个点 2 和 5 的度为 1,连边:

至此,一个 Purfer Sequence 得到的树画出来了,由上面的步骤可知,Purfer Sequence 和一个树唯一对应
综上,一个 Purfer Sequence 和一棵树一一对应
那么其数只要求出来合法的purfer sequence的数量就是生成树的数量。
将树转化为prufer编码:
n为树的节点数,d[i]为各节点的度数,(注意计算tot的时候只计算d[i]!=-1的数)m为无限制度数的节点数。
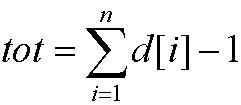
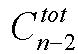 种插法;
种插法;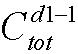 种插法;
插第二个节点的方法有
种插法;
插第二个节点的方法有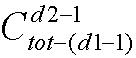 种插法;………
种插法;………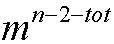 ;
;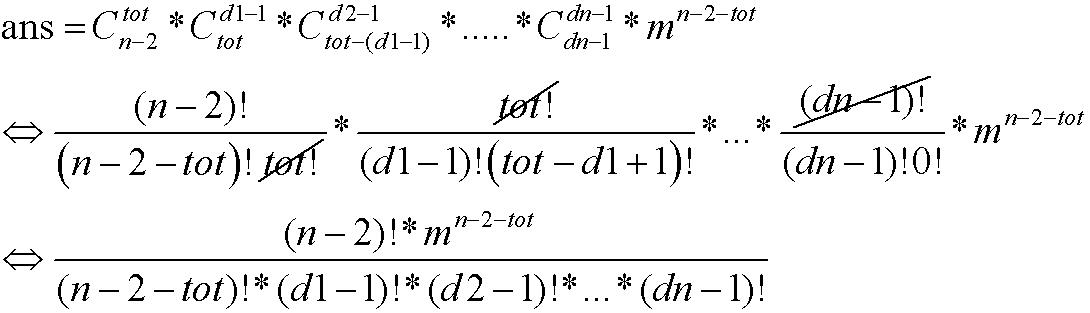
基本上知道什么是purfer_sequence这道题就没问题了.然后就是组合数学的推导.由于要用高精度,除法不太方便,我是直接暴力分解因数,然后坐指数相加减...最后来一发快速幂.
p.s.
1.按理来说应该要特判无解的情况,但是没有特判也A了...

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int maxn=1000+5,maxl=500,base=100000000; 5 int n,cnt,sum; 6 int s[maxn],c[maxn]; 7 typedef long long ll; 8 9 struct Bign{ 10 int cnt; ll x[maxl]; 11 Bign(int t=0){ 12 memset(x,0,sizeof x); 13 x[cnt=1]=t; 14 } 15 ll & operator [](int id){ return x[id]; } 16 }ans(1); 17 Bign operator *= (Bign &x,Bign &y){ 18 Bign z; 19 for(int i=1;i<=x.cnt;i++)for(int j=1;j<=y.cnt;j++) 20 z[i+j-1]+=x[i]*y[j], z[i+j]+=z[i+j-1]/base, z[i+j-1]%=base; 21 z.cnt=x.cnt+y.cnt; 22 if(!z[z.cnt]) z.cnt--; 23 x=z; 24 } 25 ostream & operator << (ostream &out,Bign &x){ 26 printf("%lld",x[x.cnt]); 27 for(int i=x.cnt-1;i;i--) printf("%08lld",x[i]); 28 return out; 29 } 30 void decomposition(int x,int y){ 31 for(int i=2;i*i<=x;i++)while(x%i==0) c[i]+=y, x/=i; 32 if(x^1) c[x]+=y; 33 } 34 void quick_power(int i,int y){ 35 Bign x(i); 36 for(;y;x*=x, y>>=1) if(y&1) ans*=x; 37 } 38 int main(){ 39 freopen("bzoj_1005.in","r",stdin); 40 freopen("bzoj_1005.out","w",stdout); 41 scanf("%d",&n); 42 for(int i=1;i<=n;i++){ 43 int t; scanf("%d",&t); 44 if(t>0) s[++cnt]=t-1, sum+=t-1; 45 } 46 for(int i=2;i<=n-2;i++) decomposition(i,1); 47 for(int i=1;i<=cnt;i++)for(int j=2;j<=s[i];j++) decomposition(j,-1); 48 for(int i=2;i<=n-2-sum;i++) decomposition(i,-1); 49 decomposition(n-cnt,n-2-sum); 50 for(int i=2;i<=n;i++)if(c[i]) quick_power(i,c[i]); 51 cout<<ans<<endl; 52 return 0; 53 }
1005: [HNOI2008]明明的烦恼
Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 3980 Solved: 1583
[Submit][Status][Discuss]
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
1
-1
-1
Sample Output
HINT
两棵树分别为1-2-3;1-3-2
Source
以上是关于BZOJ_1005_ [HNOI2008]_明明的烦恼_(组合数学+purfer_sequence+高精度+分解因数)的主要内容,如果未能解决你的问题,请参考以下文章
BZOJ1005--[HNOI2008]明明的烦恼(树的prufer编码)
