10.STL简单红黑树的实现
Posted chengonghao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了10.STL简单红黑树的实现相关的知识,希望对你有一定的参考价值。
1.红黑树简介
二叉搜索树能够提供对数的元素插入和访问。二叉搜索树的规则是:任何节点的键值一定大于其左子树的每一个节点值,并小于右子树的每一个节点值。
常见的二叉搜索树有AVL-tree、RB-tree(红黑树)。红黑树具有极佳的增、删、查性能,故我们选择红黑树作为关联式容器(associative containers)的底层结构。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
1. 节点是红色或黑色。;
2. 根节点是黑色;
3. 每个叶节点(NILL节点,空节点)是黑色的;
4. 每个红色节点的两个子节点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色节点);
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
由性质4可以推出:一条路径上不能有两个毗连的红色节点。最短的可能路径都是黑色节点,最长的可能路径是交替的红色和黑色节点。又根据性质5,所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
以上约束条件强化了红黑树的关键性质: 从根到叶子的最长路径不多于最短路径的两倍长。所以红黑树是大致上是平衡的(不像AVL-tree,要求绝对平衡)。树的插入、删除和查找效率与树的高度成比例,红黑树的高度上限允许在最坏情况下都是高效的,这是红黑树相对于其他二叉搜索树最大的优势。
2.红黑树在STL中的实现
要学习STL关联式容器,我们必须实现一颗红黑树。本文介绍红黑树在STL中的代码实现,为今后学习关联式容器打下基础。关于红黑树的详细特性(如增加、删除、旋转等)不在讨论范围内,请查阅相关资料。
我用VS2013写的程序(github),红黑树版本的代码位于cghSTL/version/cghSTL-0.4.0.rar
一颗STL红黑树的实现需要以下几个文件:
1. globalConstruct.h,构造和析构函数文件,位于cghSTL/allocator/cghAllocator/
2. cghAlloc.h,空间配置器文件,位于cghSTL/allocator/cghAllocator/
3. rb_tree_node.h,红黑树节点,位于cghSTL/associative containers/RB-tree/
4. rb_tree_iterator.h,红黑树迭代器,位于cghSTL/associative containers/RB-tree/
5. rb_tree.h,红黑树的实现,位于cghSTL/associative containers/RB-tree/
6. test_rb_tree.cpp,红黑树的测试,位于cghSTL/test/
2.1构造与析构
先看第一个,globalConstruct.h构造函数文件
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 功能:全局构造和析构的实现代码
******************************************************************/
#include "stdafx.h"
#include <new.h>
#include <type_traits>
#ifndef _CGH_GLOBAL_CONSTRUCT_
#define _CGH_GLOBAL_CONSTRUCT_
namespace CGH
{
#pragma region 统一的构造析构函数
template<class T1, class T2>
inline void construct(T1* p, const T2& value)
{
new (p)T1(value);
}
template<class T>
inline void destroy(T* pointer)
{
pointer->~T();
}
template<class ForwardIterator>
inline void destroy(ForwardIterator first, ForwardIterator last)
{
// 本来在这里要使用特性萃取机(traits编程技巧)判断元素是否为non-trivial
// non-trivial的元素可以直接释放内存
// trivial的元素要做调用析构函数,然后释放内存
for (; first < last; ++first)
destroy(&*first);
}
#pragma endregion
}
#endif按照STL的接口规范,正确的顺序是先分配内存然后构造元素。构造函数的实现采用placement new的方式;为了简化起见,我直接调用析构函数来销毁元素,而在考虑效率的情况下一般会先判断元素是否为non-trivial类型。
关于 trivial 和 non-trivial 的含义,参见:stack overflow
2.2空间配置器
cghAlloc.h是空间配置器文件,空间配置器负责内存的申请和回收。
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 功能:cghAllocator空间配置器的实现代码
******************************************************************/
#ifndef _CGH_ALLOC_
#define _CGH_ALLOC_
#include <new>
#include <cstddef>
#include <cstdlib>
#include <climits>
#include <iostream>
namespace CGH
{
#pragma region 内存分配和释放函数、元素的构造和析构函数
// 内存分配
template<class T>
inline T* _allocate(ptrdiff_t size, T*)
{
set_new_handler(0);
T* tmp = (T*)(::operator new((size_t)(size * sizeof(T))));
if (tmp == 0)
{
std::cerr << "out of memory" << std::endl;
exit(1);
}
return tmp;
}
// 内存释放
template<class T>
inline void _deallocate(T* buffer)
{
::operator delete(buffer);
}
// 元素构造
template<class T1, class T2>
inline void _construct(T1* p, const T2& value)
{
new(p)T1(value);
}
// 元素析构
template<class T>
inline void _destroy(T* ptr)
{
ptr->~T();
}
#pragma endregion
#pragma region cghAllocator空间配置器的实现
template<class T>
class cghAllocator
{
public:
typedef T value_type;
typedef T* pointer;
typedef const T* const_pointer;
typedef T& reference;
typedef const T& const_reference;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
template<class U>
struct rebind
{
typedef cghAllocator<U> other;
};
static pointer allocate(size_type n, const void* hint = 0)
{
return _allocate((difference_type)n, (pointer)0);
}
static void deallocate(pointer p, size_type n)
{
_deallocate(p);
}
static void deallocate(void* p)
{
_deallocate(p);
}
void construct(pointer p, const T& value)
{
_construct(p, value);
}
void destroy(pointer p)
{
_destroy(p);
}
pointer address(reference x)
{
return (pointer)&x;
}
const_pointer const_address(const_reference x)
{
return (const_pointer)&x;
}
size_type max_size() const
{
return size_type(UINT_MAX / sizeof(T));
}
};
#pragma endregion
#pragma region 封装STL标准的空间配置器接口
template<class T, class Alloc = cghAllocator<T>>
class simple_alloc
{
public:
static T* allocate(size_t n)
{
return 0 == n ? 0 : (T*)Alloc::allocate(n*sizeof(T));
}
static T* allocate(void)
{
return (T*)Alloc::allocate(sizeof(T));
}
static void deallocate(T* p, size_t n)
{
if (0 != n)Alloc::deallocate(p, n*sizeof(T));
}
static void deallocate(void* p)
{
Alloc::deallocate(p);
}
};
#pragma endregion
}
#endifclasscghAllocator是空间配置器类的定义,主要的四个函数的意义如下:allocate函数分配内存,deallocate函数释放内存,construct构造元素,destroy析构元素。这四个函数最终都是通过调用_allocate、_deallocate、_construct、_destroy这四个内联函数实现功能。
我们自己写的空间配置器必须封装一层STL的标准接口,
template<classT,class Alloc = cghAllocator<T>>
classsimple_alloc构造与析构函数、空间配置器是STL中最最基本,最最底层的部件,把底层搭建好之后我们就可以着手设计红黑树了。
2.3 红黑树节点的实现
我们把红黑树的节点为双层结构,有基层节点(__rb_tree_node_base)和正规节点(__rb_tree_node),正规节点由基层节点继承而来。
基层节点和正规节点分工明确:基层节点包含父指针、左指针、右指针、节点颜色这四个变量,保存着节点的状态信息;正规节点不保存状态信息,仅包含节点值的信息。
布尔值定义节点颜色,红色为false,黑色为true。
基层节点和正规节点的关系如下图所示。
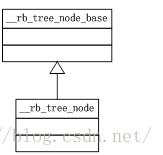
节点代码的注释已经写得十分详细了,有疑问的地方我都给出了说明。
rb_tree_node.h
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 文件内容:红黑树的节点
******************************************************************/
#ifndef _CGH_RB_TREE_NODE_
#define _CGH_RB_TREE_NODE_
namespace CGH{
typedef bool __rb_tree_color_type; // 用布尔类型定义红黑树的颜色
const __rb_tree_color_type __rb_tree_red = false; // 红色为0
const __rb_tree_color_type __rb_tree_black = true; // 黑色为1
/* 基层节点 */
struct __rb_tree_node_base{
typedef __rb_tree_color_type color_type; // 节点颜色
typedef __rb_tree_node_base* base_ptr; // 节点指针
color_type color; // 节点颜色
base_ptr parent; // 父节点指针
base_ptr left; // 左子节点指针
base_ptr right; // 右子节点指针
/*
给定某个节点位置,找到最左边的节点
如果给定根节点的位置,可以找到整颗红黑树最左边的节点(也就是找到了最小值节点)
返回节点位置
*/
static base_ptr minimum(base_ptr x)
{
while (x->left != 0)
{
x = x->left; // 一直向左走,就能找到最小节点
}
return x;
}
/*
给定某个节点位置,找到最右边的节点
如果给定根节点的位置,可以找到整颗红黑树最右边的节点(也就是找到了最大值节点)
返回节点位置
*/
static base_ptr maximum(base_ptr x)
{
while (x->right != 0)
{
x = x->right; // 一直向左右走,就能找到最大节点
}
return x;
}
};
/* 正规节点 */
template<class value>
struct __rb_tree_node :public __rb_tree_node_base{
/* 子类继承了父类的成员:color、parent、left、right,value_field用来表示节点的值域 */
typedef __rb_tree_node<value>* link_type;
value value_field; // 节点值域
};
}
#endif
2.4 红黑树迭代器的实现
与节点一样,迭代器也是双层结构。分别为基层迭代器(rb_tree_base_iterator)和正规迭代器(__rb_tree_iterator)。正规迭代器由基层迭代器继承而来。
两者分工明确:基层迭代器保存唯一的成员变量:树节点,该变量是联系迭代器和树节点的纽带;正规迭代器不包含任何成员变量,只实现迭代器的各种操作。
注意,红黑树的迭代器提供的是bidirectional access,支持双向访问,不支持随机访问。

下图总结了迭代器与红黑树节点间的关系:
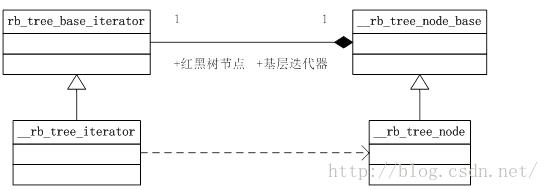
迭代器代码的注释已经写得十分详细了,有疑问的地方我都给出了说明,童鞋们可以通过注释来理解迭代器的工作原理。
rb_tree_iterator.h
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 文件内容:红黑树的迭代器
******************************************************************/
#ifndef _CGH_RB_TREE_ITERATOR_
#define _CGH_RB_TREE_ITERATOR_
#include "rb_tree_node.h"
#include <memory> // 使用ptrdiff_t需包含此头文件
namespace CGH{
/* 基层迭代器 */
struct rb_tree_base_iterator
{
typedef __rb_tree_node_base::base_ptr base_ptr; // 父类节点指针
typedef std::bidirectional_iterator_tag iterator_category;
typedef ptrdiff_t difference_type;
base_ptr node; // 成员变量:指向父类节点的指针,这是联系迭代器和节点的纽带
/* 迭代器的子类实现operator++时调用本函数 */
void increment()
{
if (node->right != 0) // 如果有右子节点
{
node = node->right; // 就向右走
while (node->left != 0) // 然后一直往左子树走到底
{
node = node->left;
}
}
else // 没有右子节点
{
base_ptr y = node->parent; // 找出父节点
while (node == y->right) // 如果现行节点本身是个右子节点
{
node = y; // 就一直上溯,直到“不为右子节点”为止
y = y->parent;
}
if (node->right != y) // 若此时的右子节点不等于此时的父节点,此时的父节点即为解答
{ // 否则此时的node为解答
node = y;
}
}
}
/* 迭代器的子类实现operator--时调用本函数 */
void decrement()
{
if (node->color == __rb_tree_red&&node->parent->parent == node)
{
// 如果是红节点,且祖父节点等于自己,那么右节点即为解答
// 该情况发生于node为header时,注意,header的右子节点(即mostright),指向整棵树的max节点
node = node->right;
}
else if (node->left != 0) // 如果有左子节点,当y
{
base_ptr y = node->left; // 令y指向左子节点
while (y->right != 0) // 当y有右子节点时
{
y = y->right; // 一直往右子节点走到底
}
node = y; // 最后即为答案
}
else // 即非根节点,也没有左子节点
{
base_ptr y = node->parent; // 找出父节点
while (node == y->left) // 当现行节点为左子节点
{
node = y; // 一直交替往上走,直到现行节点
y = y->parent; // 不为左子节点
}
node = y; // 此时父节点即为答案
}
}
};
/* 正规迭代器 */
template<class value,class ref,class ptr>
struct __rb_tree_iterator :public rb_tree_base_iterator
{
#pragma region typedef
/*
注意,正规迭代器没有成员变量,只继承了基层迭代器的node变量
基层迭代器的node变量是红黑树节点与迭代器连接的纽带
*/
typedef value value_type;
typedef ref reference;
typedef ptr pointer;
typedef __rb_tree_iterator<value, value&, value*> iterator;
typedef __rb_tree_iterator<value, ref, ptr> self;
typedef __rb_tree_node<value>* link_type;
typedef size_t size_type;
#pragma endregion
#pragma region 构造函数
__rb_tree_iterator(){} // default构造函数
__rb_tree_iterator(link_type x){ node = x; } // 普通构造函数
__rb_tree_iterator(const iterator& it){ node = it.node; } // copy构造函数
#pragma endregion
#pragma region 迭代器的基本操作
/* 解除引用,返回节点值 */
reference operator*()const{ return link_type(node)->value_field; }
/* 解除引用,返回节点值 */
pointer operator->()const{ return *(operator*()); }
/* 返回迭代器指向的节点的颜色 */
__rb_tree_color_type color(){ return node->color == __rb_tree_red ? 0 : 1; }
/* 迭代器步进 */
self& operator++()const{ increment(); return *this; }
/* 迭代器步进 */
self& operator++(int)
{
self tmp = *this;
increment();
return tmp;
}
/* 迭代器步退 */
self& operator--()const{ decrement(); return *this; }
/* 迭代器步退 */
self& operator--(int)
{
self tmp = *this;
decrement();
return tmp;
}
/* 比较两迭代器是否指向同一个节点 */
bool operator==(const self& x)const{ return x.node == node; }
/* 比较两迭代器是否指向同一个节点 */
bool operator!=(const self& x)const{ return x.node != node; }
#pragma endregion
};
}
#endif2.5 红黑树的实现
有了红黑树的节点和迭代器,接下来着手设计红黑树。
红黑树的内部结构我用region分为了以下部分:
1. 一堆typedef;
2. 红黑树的成员变量:节点数目(node_count)、迭代器(iterator)等;
3. 树的初始化,节点的构造、析构、复制;
4. 受保护的辅助函数,作为内部工具;
5. 红黑树的操作;
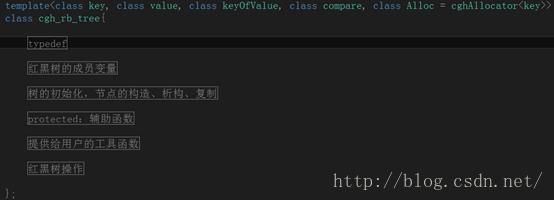
注意,我们在红黑树中使用了一个名为header的节点,header节点作为哨兵,本身不是红黑树的一部分。
header节点的作用有三个:
1. 标识根节点的位置;
2. 标识红黑树最左边节点的位置
3. 标识红黑树最右边节点的位置
红黑树实现代码的注释已经写得十分详细了,有疑问的地方我都给出了说明,童鞋们可以参考红黑树的内部结构来总体把握红黑树的框架,通过注释来理解红黑树的工作原理。
rb_tree.h:
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 文件内容:红黑树
******************************************************************/
#ifndef _CGH_RB_TREE_
#define _CGH_RB_TREE_
#include "globalConstruct.h" // 全局构造析构函数
#include "cghAlloc.h" // 空间配置器
#include "rb_tree_node.h" // 红黑树节点
#include "rb_tree_iterator.h" // 红黑树迭代器
#include <memory> // 使用ptrdiff_t需包含此头文件
namespace CGH{
template<class key, class value, class keyOfValue, class compare, class Alloc = cghAllocator<key>>
class cgh_rb_tree{
#pragma region typedef
protected:
typedef void* void_pointer; // 空指针
typedef __rb_tree_node_base* base_ptr; // 基层节点指针
typedef __rb_tree_node<value> rb_tree_node; // 正规节点指针
typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator; // 节点空间配置器
typedef __rb_tree_color_type color_type; // 节点颜色
public:
typedef key key_type; // 键
typedef value value_type; //值
typedef value_type* pointer; // 值指针
typedef const value_type* const_pointer; // const值指针
typedef value_type& reference; // 值引用
typedef const value_type& const_reference; // const值引用
typedef rb_tree_node* link_type; // 节点指针
typedef size_t size_type;
typedef ptrdiff_t difference_type;
#pragma endregion
#pragma region 红黑树的成员变量
protected:
size_type node_count; // 红黑树的节点数目
link_type header; // 哨兵节点,其parent指针指向根节点
compare key_compare; // 比较值大小的函数
public:
typedef __rb_tree_iterator<value_type, reference, pointer> iterator; // 定义红黑树的迭代器
#pragma endregion
#pragma region 树的初始化,节点的构造、析构、复制
protected:
/* 调用空间配置器申请一个节点 */
link_type get_node(){ return rb_tree_node_allocator::allocate(); }
/* 调用空间配置器释还一个节点 */
void put_node(link_type p){ rb_tree_node_allocator::deallocate(p); }
/* 申请并初始化节点 */
link_type create_node(const value_type& x)
{
// x是节点的值
link_type tmp = get_node(); // 申请一个节点
construct(&tmp->value_field, x); // 调用全局构造函数初始化节点
return tmp;
}
/* 克隆节点 */
link_type clone_node(link_type x)
{
link_type tmp = create_node(x->value_field); // 申请并初始化节点
tmp->color = x->color;
tmp->left = 0;
tmp->right = 0;
return tmp;
}
/* 释还节点 */
void destroy_node(link_type p)
{
destroy(&p->value_field); // 调用全局析构函数销毁节点值
put_node(p); // 释还内存
}
private:
/* 初始化红黑树 */
void init()
{
header = get_node(); // 初始化header节点,header节点作为整颗红黑树的哨兵,header的parent指针指向根节点,header的类型是__rb_tree_node*
color(header) = __rb_tree_red; // 设置header节点为红色
root() = 0; // root()获得红黑树的根节点,header的parent指针指向根节点,初始化红黑树的根节点指针为null
leftmost() = header; // 设置header节点的左子树指向自己
rightmost() = header; // 设置header节点的右子树指向自己
}
public:
/* 构造函数 */
cgh_rb_tree(const compare& cmp = compare()) :node_count(0), key_compare(cmp){ init(); }
/* 析构函数 */
~cgh_rb_tree()
{
//clear();
put_node(header);
}
#pragma endregion
#pragma region protected:辅助函数
protected:
/* 获得根节点(header是哨兵,其parent执行根节点) */
link_type& root()const{ return (link_type&)header->parent; }
/* 获得整棵树最左边的节点 */
link_type& leftmost()const{ return (link_type&)header->left; }
/* 获得整棵树最右边的节点 */
link_type& rightmost()const{ return (link_type&)header->right; }
/* 返回节点的左子节点 */
static link_type& left(link_type x){ return (link_type&)(x->left); }
/* 返回节点的右子节点 */
static link_type& right(link_type x){ return (link_type&)(x->right); }
/* 返回节点的父节点 */
static link_type& parent(link_type x){ return (link_type&)(x->parent); }
/* 返回节点的value */
static reference value(link_type x){ return (x->value_field); }
/* 返回节点的颜色 */
static color_type& color(link_type x){ return (color_type)(x->color); }
/* 返回节点的value */
static const key& key(base_ptr x){ return keyOfValue()(value(link_type(x))); }
/* 返回最小值节点 */
static link_type minimum(link_type x)
{
return (link_type)__rb_tree_node_base::minimum(x); // 调用基层节点的最小节点函数
}
/* 返回最大值节点 */
static link_type maximum(link_type x)
{
return (link_type)__rb_tree_node_base::maximum(x); // 调用基层节点的最大节点函数
}
#pragma endregion
#pragma region 提供给用户的工具函数
public:
/* 获得根节点的值(header是哨兵,其parent执行根节点); return (link_type&)header->parent->; */
value_type root_value(){ return value((link_type)header->parent); }
/* 返回比较大小的函数 */
compare key_comp()const{ return key_compare; }
/* 返回一个迭代器,指向红黑树最左边的节点 */
iterator begin(){ return leftmost(); }
/* 返回一个迭代器,指向红黑树最右边的节点 */
iterator end(){ return header; }
/* 判断红黑树是否为空 */
bool empty()const{ return node_count == 0; }
/* 返回红黑树大小(节点数目) */
size_type size() const{ return node_count; }
/* 红黑树最大节点数 */
size_type max_size()const{ return size_type(-1); }
#pragma endregion
#pragma region 红黑树操作
public:
/*
插入新值,节点键值不能重复,如果重复则插入无效
返回值是pair,pair的第一个元素是rb_tree迭代器,指向新节点
第二个元素表示插入成功与否
*/
std::pair<iterator, bool> insert_unique(const value_type& v)
{
link_type y = header; // link_type的类型是__rb_tree_node*,header是哨兵,令y拿到header
link_type x = root(); // x拿到红黑树的根节点,红黑树的根节点被初始化为null,因此插入第一个值时,x等于null
bool comp = true; // 比较大小的布尔值
while (x != 0) // x节点不为null,说明我们找到插入新节点的位置,于是执行while循环内的语句,不停向下遍历
{
y = x; // y保存着x节点的父节点
// 如果待插入的值小于节点x的值,comp为true,否则comp为false。key_compare是比较大小的函数(由模板指定)
comp = key_compare(keyOfValue()(v), key(x));
// 如果comp为true,说明待插入值小于节点x的值,我们沿左走,令x为x的左子树
// 如果comp为false,说明待插入值大于节点x的值,我们沿右走,令x为x的右子树
x = comp ? left(x) : right(x);
}
iterator j = iterator(y); // 令j指向插入点的父节点
if (comp) // 如果插入的值比父节点的值小(意味着我们要插入到父节点的左边),进入if
{
// begin()调用leftmost(),获得整颗树最左侧的节点,如果插入节点为整颗树的最左侧节点就进入if
if (begin() == j)
{
return std::pair<iterator, bool>(__insert(x, y, v), true); // x是插入点、y为插入点的父节点,v为插入的值
}
else
{
j--;
}
}
// 新值不与既有节点值重复,可以插入
if (key_compare(key(j.node), keyOfValue()(v)))
{
return std::pair<iterator, bool>(__insert(x, y, v), true);
}
return std::pair<iterator, bool>(j, false); // 如果到了这里,说明新值一定与树中键值重复,不能插入
}
/*
插入新值,节点的键值允许重复
返回红黑树的迭代器,该迭代器指向新节点
*/
iterator insert_equal(const value_type& v)
{
link_type y = header;
link_type x = root(); // x指向根节点
while (x != 0) // 从根节点开始向下寻找合适的插入点
{
y = x;
// 遇大往右,遇小往左
x = key_compare(keyOfValue()(v), key(x)) ? left(x) : right(x);
}
return __insert(x, y, v); // x为待插入点,y为插入点的父节点,v为插入的值
}
/* 寻找红黑树中是否有键值为k的节点 */
iterator find(const value_type& k)
{
link_type y = header; // 令y等于哨兵节点(哨兵节点不是树的一部分,但是其parent指向根节点)
link_type x = root(); // 拿到根节点
while (x != 0)
{
// key_compare是比较大小的函数
if (!key_compare(key(x), k)) // x值大于k
{
y = x;
x = left(x); // 遇到大值就向左走
}
else // x值与于k
{
x = right(x); // 遇到小值往左走
}
}
iterator j = iterator(y);
return (j == end() || key_compare(k, key(j.node))) ? end() : j;
}
private:
/*
插入操作
x_:待插入节点
y_:插入节点的父节点
v:插入的值
*/
iterator __insert(base_ptr x_, base_ptr y_, const value_type& v)
{
// base_ptr实为__rb_tree_node_base*,link_type实为__rb_tree_node*
// 我们把__rb_tree_node_base*向下强转为__rb_tree_node*
// __rb_tree_node结构体比__rb_tree_node_base结构体多了value_field,value_field用于保存值
link_type x = (link_type)x_; // x指向插入点
link_type y = (link_type)y_; // y指向插入点的父节点
link_type z;
// 1.y == header:插入点的父节点为header(注意header是哨兵,header不属于树的一部分,但是header的parent指向根节点)。y == header说明插入点为根节点
// 2.x == 0:说明插入点在叶子节点下方(叶子节点的左子树和右子树均为null),也就是在叶子节点下挂新的节点;x != 0说明插入点在树的内部某个节点上
// 3.key_compare(keyOfValue()(v), key(y)):带插入节点的值要比父节点的值小(意味着我们要插入到父节点的左子树上)
if (y == header || x != 0 || key_compare(keyOfValue()(v), key(y)))
{
z = create_node(v); // 创建新节点,令新节点的值(value_field)为v
left(y) = z; // 令父节点的左子树为z,我们成功的把新节点加入到树中了
if (y == header) // y == header:插入点的父节点为header,说明根节点还没有被初始化,进入if就是要初始化根节点
{
root() = z; // z成了根节点
rightmost() = z; // 令z为整棵树最右边的节点
}
else if (y == leftmost()) // 如果父节点是整颗树最左边的节点
{
leftmost() = z; // 我们把新节点作为整棵树最左边的节点
}
}
else
{
z = create_node(v); // 创建新节点
right(y) = z; // 插入节点到父节点的右边
if (y == rightmost()) // 如果父节点是整颗树最右边的节点
{
rightmost() = z; // 我们把新节点作为整棵树最右边的节点
}
}
parent(z) = y; // 令新节点的父节点为y
left(z) = 0; // 新节点的左子树为null
right(z) = 0; // 新节点的右子树为null
__rb_tree_rebalance(z, header->parent); // header是哨兵,一旦建立就不改变,header->parent执行树的根节点
++node_count; // 增加节点数
return iterator(z);
}
/*
重新平衡红黑树(改变颜色和旋转树形)
x是新增节点
root为根节点
*/
inline void __rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
x->color = __rb_tree_red; // 新插入的节点是红色的
// 如果新增节点(x)不为根节点,且新增节点的父节点为红色,那麻烦就大了,要进入while一顿折腾
while (x != root && x->parent->color == __rb_tree_red)
{
if (x->parent == x->parent->parent->left) // 如果父节点是祖父节点的左子节点
{
__rb_tree_node_base* y = x->parent->parent->right; // 令y为伯父节点
if (y && y->color == __rb_tree_red) // 如果伯父节点存在且为红
{
x->parent->color = __rb_tree_black;
y->color = __rb_tree_black;
x->parent->parent->color = __rb_tree_red;
x = x->parent->parent;
}
else // 如果伯父节点不存在,或者伯父节点为黑
{
if (x == x->parent->right) // 如果新增节点为父节点的右子节点(为父节点的右子节点,这说明插入节点的方式是内插)
{
x = x->parent; // 父节点为旋转支点
// 整理一下从while开始的条件判断分支,我们可以得出做左旋转的条件:
// 1.新增节点不是根节点
// 2.新增节点的父节点是红色
// 3.父节点是祖父节点的左子节点
// 4.伯父节点不存在,或者伯父节点为黑
// 5.新增节点为父节点的右子节点
__rb_tree_rotate_left(x, root); // 做左旋转
}
x->parent->color = __rb_tree_black; // 修改颜色
x->parent->parent->color = __rb_tree_red; // 修改颜色
__rb_tree_rotate_right(x->parent->parent, root); // 左旋完了接着右旋
}
}
else // 如果父节点是祖父节点的右子节点
{
__rb_tree_node_base* y = x->parent->parent->left; // 令y为伯父节点
if (y && y->color == __rb_tree_red) // 如果伯父节点存在且为红
{
x->parent->color = __rb_tree_black;
y->color = __rb_tree_black;
x->parent->parent->color = __rb_tree_red;
x = x->parent->parent;
}
else // 如果伯父节点不存在,或者伯父节点为黑
{
// 如果新增节点为父节点的左子节点(为父节点的左子节点,这说明插入节点的方式是内插)
if (x == x->parent->left)
{
x = x->parent; // 父节点为旋转支点
// 整理一下从while开始的条件判断分支,我们可以得出做右旋转的条件:
// 1.新增节点不是根节点
// 2.新增节点的父节点是红色
// 3.父节点是祖父节点的右子节点
// 4.伯父节点不存在,或者伯父节点为黑
// 5.新增节点为父节点的左子节点
__rb_tree_rotate_right(x, root); // 做右旋转
}
x->parent->color = __rb_tree_black; // 修改颜色
x->parent->parent->color = __rb_tree_red; // 修改颜色
__rb_tree_rotate_left(x->parent->parent, root); // 右旋完了接着左旋
}
}
}
root->color = __rb_tree_black; // 树的根节点永远是黑
}
/*
左旋转
新节点比为红节点,如果插入节点的父节点也为共色,就违反了红黑树规则,此时必须做旋转
x:左旋转的支点
root:红黑树的根
*/
inline void __rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
__rb_tree_node_base* y = x->right; // y为旋转点的右子节点
x->right = y->left; // 旋转点为父,旋转点的右子节点为子,完成父子对换
if (y->left != 0)
{
y->left->parent = x;
}
y->parent = x->parent;
if (x == root)
{
root = y; // 令y为根节点
}
else if (x == x->parent->left)
{
x->parent->left = y; // 令旋转点的父节点的左子节点为y
}
else
{
x->parent->right = y; // 令旋转点的父节点的右子节点为y
}
y->left = x; // 右子节点的左子树为x
x->parent = y; // 右子节点为旋转点的父节点
}
/*
右旋转
新节点比为红节点,如果插入节点的父节点也为共色,就违反了红黑树规则,此时必须做旋转
x:右旋转的支点
root:红黑树的根
*/
inline void __rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
__rb_tree_node_base* y = x->left; // 令y为旋转点的左子节点
x->left = y->right; // 令y的右子节点为旋转点的左子节点
if (y->right != 0)
{
y->right->parent = x; // 设定父节点
}
y->parent = x->parent;
// 令y完全顶替x的地位(必须将对其父节点的关系完全接收过来)
if (x == root)
{
root = y; // x为根节点
}
else if (x == x->parent->right)
{
x->parent->right = y; // x为其父节点的右子节点
}
else
{
x->parent->left = y; // x为其父节点的左子节点
}
y->right = x;
x->parent = y;
}
#pragma endregion
};
}
#endif
3.测试
3.1 测试用例
测试代码,test_rb_tree.cpp:
/*******************************************************************
* Copyright(c) 2016 Chen Gonghao
* All rights reserved.
*
* chengonghao@yeah.net
*
* 文件内容:红黑树的测试
******************************************************************/
#include "stdafx.h"
#include "rb_tree.h"
using namespace::std;
int _tmain(int argc, _TCHAR* argv[])
{
using namespace::CGH;
cgh_rb_tree<int, int, identity<int>, less<int>> test;
test.insert_unique(10);
test.insert_unique(7);
test.insert_unique(8);
test.insert_unique(15);
test.insert_unique(5);
test.insert_unique(6);
test.insert_unique(11);
test.insert_unique(13);
test.insert_unique(12);
cgh_rb_tree<int, int, identity<int>, less<int>>::iterator it = test.begin();
int i = 1;
for (; it != test.end(); it++)
{
string color = it.color() == true ? "黑" : "红";
std::cout << *it << " ( " << color.c_str() << " )" << endl << endl;
}
std::cout << "树的根节点:" << test.root_value()<< endl << endl;
std::cout << "树的大小:" << test.size() << endl << endl;
system("pause");
return 0;
}
测试图:

根据测试图可以画出红黑树:
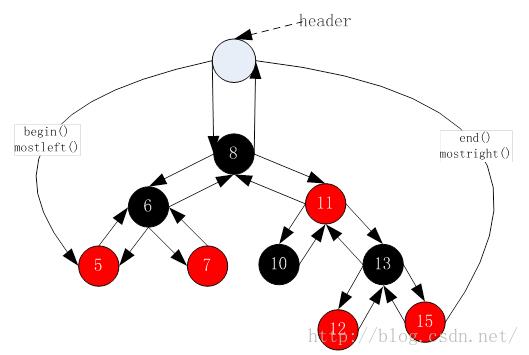
header是哨兵节点,有三个作用:
1. 标识根节点的位置;
2. 标识红黑树最左边节点的位置
3. 标识红黑树最右边节点的位置
3.2 分析一个节点的插入
我们举例分析8插入红黑树的过程。
1. 插入8之前,红黑树的样子:

2. 8小于10,大于7,应该插在7的右子树上

这明显违反了红黑树的规定:红的下面不能挂红的,节点8的伯父节点(10的右子节点)为黑色(空节点为黑色),我们以7为支点,对7、8两节点做左旋转。为方便起见,令7为x,8为y。
3. 左旋第一步(左旋操作均在__rb_tree_rotate_left函数内)
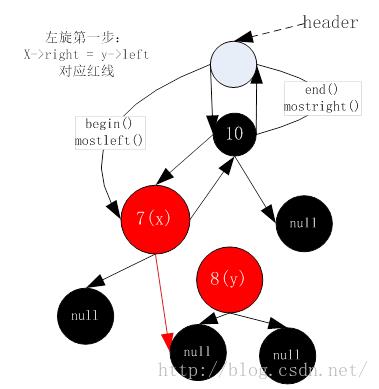
4. 左旋第二步(左旋操作均在__rb_tree_rotate_left函数内)
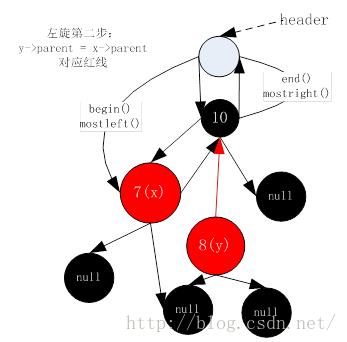
5. 左旋第三步(左旋操作均在__rb_tree_rotate_left函数内)
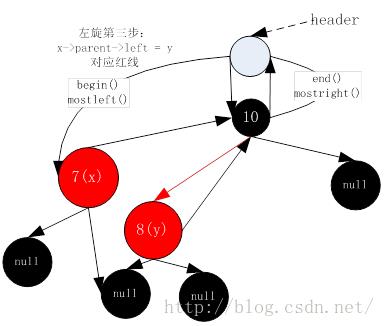
6. 左旋第四步(左旋操作均在__rb_tree_rotate_left函数内)

7. 左旋第五步(左旋操作均在__rb_tree_rotate_left函数内)

左旋结束,我们先改变节点颜色(对应代码在__rb_tree_rebalance函数中):
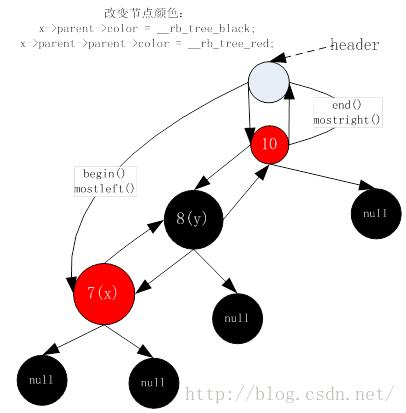
根节点不能为红色,我们还需要做右旋,把节点8作为根节点。
8. 右旋第一步(右旋操作均在__rb_tree_rotate_right函数内),令根节点为x,节点8为y
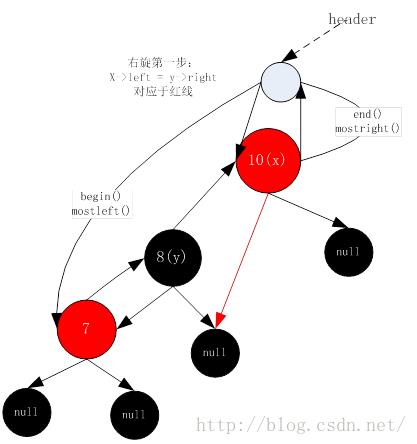
9. 右旋第二步(右旋操作均在__rb_tree_rotate_right函数内)
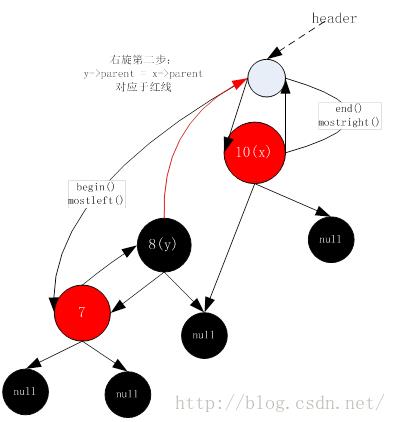
10. 右旋第三步(右旋操作均在__rb_tree_rotate_right函数内)

11. 右旋第四步(右旋操作均在__rb_tree_rotate_right函数内)

12. 右旋第五步(右旋操作均在__rb_tree_rotate_right函数内)
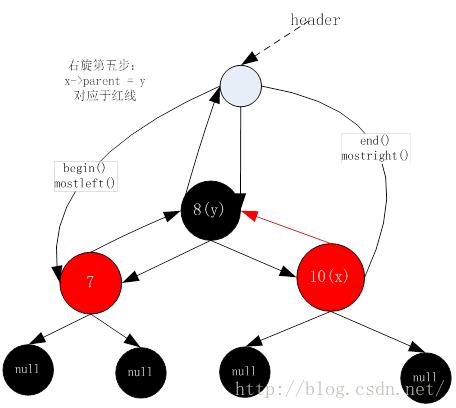
到此为止,红黑树又恢复平衡啦~
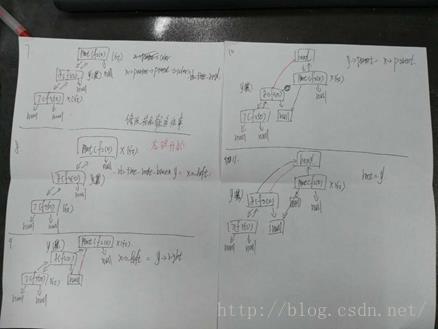
以下是我理解插入操作时边打断点边画的图,纪念一下:

以上是关于10.STL简单红黑树的实现的主要内容,如果未能解决你的问题,请参考以下文章