使用Muduo完成数独和八数码问题求解服务器

Posted 2020-07-16 NK_test

在剖析完Muduo网络库源码之后，我们试着完成一个高效的数独和八数码问题求解服务器。

先说说为什么要选择这两个问题？数独问题一直是陈硕老师很喜欢的问题，在muduo网络库中多次提到并有示例。八数码问题是我很喜欢的问题，所以在此综合完成求解数独和八数码问题的高效服务端程序。

编写这样一个看似简单的服务程序的技术含量远高于所谓的控件堆砌型开发，虽然有muduo网络库帮助我们处理网络事件，我们只需要关注setConnectionCallback() 和setMessageCallback() 事件，但是这两个问题都是cpu密集型任务，需要高效的算法，同时使用多核加速（ThreadPool）。我们采用Dancing Links算法求解数独问题，使用A* 算法+康托展开 求解八数码问题并打印操作路径。算法由我自己编写实现，同时通过online judge的测试数据（hdu 1043 ,poj  3074），正确性有一定保证。

关于这里面涉及的算法在此不再赘述，请算法基础薄弱的读者自行查看以下参考链接：

Dancing Links 算法:     http://wenku.baidu.com/link?url=ENP5vkf6Ws54iuVhEFFvnkLrgWuv_ukhVnfBUfszEifQjRzX-hXJa-laCcL6Bkos-X1SDV3uyV0vXSf2j95LrW_p_FYqkDW2Zk2LmzLCxQ3

A*算法：http://www.cnblogs.com/luxiaoxun/archive/2012/08/05/2624115.html

康托展开： http://baike.baidu.com/link?url=kBFlr76wrl2UsxzU_pNNJpCtIvOa8LSjM5_b6DI6XBhekB00ax8fR7YbkTQhbzt-dNK4v90VrlH1kujTqZazB_

（一）数独

输入的格式为81个数字，按照棋盘由左到右，由上到下来排列，前面可以加上用“：”分隔 的序号和标志，例如：

00000000000.....00000  或者  a:00000000000...00000,有解返回答案字符串，无解返回“No solution”

数独算法的核心代码类如下：

struct Node;
typedef Node Column;
struct Node
{
    Node* left;
    Node* right;
    Node* up;
    Node* down;
    Column* col;
    int name;
    int size;
};

const int kMaxNodes = 1 + 81*4 + 9*9*9*4;
// const int kMaxColumns = 400;
const int kRow = 100, kCol = 200, kBox = 300;
extern const char kNoSolution[] = "NoSolution";

class SudokuSolver
{
 public:
    SudokuSolver(int board[kCells])
      : inout_(board),
        cur_node_(0)
    {
        stack_.reserve(100);

        root_ = new_column();
        root_->left = root_->right = root_;
        memset(columns_, 0, sizeof(columns_));

        bool rows[kCells][10] = { {false} };
        bool cols[kCells][10] = { {false} };
        bool boxes[kCells][10] = { {false} };

        for (int i = 0; i < kCells; ++i) {
            int row = i / 9;
            int col = i % 9;
            int box = row/3*3 + col/3;
            int val = inout_[i];
            rows[row][val] = true;
            cols[col][val] = true;
            boxes[box][val] = true;
        }

        for (int i = 0; i < kCells; ++i) {
            if (inout_[i] == 0) {
                append_column(i);
            }
        }

        for (int i = 0; i < 9; ++i) {
            for (int v = 1; v < 10; ++v) {
                if (!rows[i][v])
                    append_column(get_row_col(i, v));
                if (!cols[i][v])
                    append_column(get_col_col(i, v));
                if (!boxes[i][v])
                    append_column(get_box_col(i, v));
            }
        }

        for (int i = 0; i < kCells; ++i) {
            if (inout_[i] == 0) {
                int row = i / 9;
                int col = i % 9;
                int box = row/3*3 + col/3;
                //int val = inout[i];
                for (int v = 1; v < 10; ++v) {
                    if (!(rows[row][v] || cols[col][v] || boxes[box][v])) {
                        Node* n0 = new_row(i);
                        Node* nr = new_row(get_row_col(row, v));
                        Node* nc = new_row(get_col_col(col, v));
                        Node* nb = new_row(get_box_col(box, v));
                        put_left(n0, nr);
                        put_left(n0, nc);
                        put_left(n0, nb);
                    }
                }
            }
        }
    }

    bool solve()
    {
        if (root_->left == root_) {
            for (size_t i = 0; i < stack_.size(); ++i) {
                Node* n = stack_[i];
                int cell = -1;
                int val = -1;
                while (cell == -1 || val == -1) {
                    if (n->name < 100)
                        cell = n->name;
                    else
                        val = n->name % 10;
                    n = n->right;
                }

                //assert(cell != -1 && val != -1);
                inout_[cell] = val;
            }
            return true;
        }

        Column* const col = get_min_column();
        cover(col);
        for (Node* row = col->down; row != col; row = row->down) {
            stack_.push_back(row);
            for (Node* j = row->right; j != row; j = j->right) {
                cover(j->col);
            }
            if (solve()) {
                return true;
            }
            stack_.pop_back();
            for (Node* j = row->left; j != row; j = j->left) {
                uncover(j->col);
            }
        }
        uncover(col);
        return false;
    }

 private:

    Column* root_;
    int*    inout_;
    Column* columns_[400];
    std::vector<Node*> stack_;
    Node    nodes_[kMaxNodes];
    int     cur_node_;

    Column* new_column(int n = 0)
    {
        assert(cur_node_ < kMaxNodes);
        Column* c = &nodes_[cur_node_++];
        memset(c, 0, sizeof(Column));
        c->left = c;
        c->right = c;
        c->up = c;
        c->down = c;
        c->col = c;
        c->name = n;
        return c;
    }

    void append_column(int n)
    {
        assert(columns_[n] == NULL);

        Column* c = new_column(n);
        put_left(root_, c);
        columns_[n] = c;
    }

    Node* new_row(int col)
    {
        assert(columns_[col] != NULL);
        assert(cur_node_ < kMaxNodes);

        Node* r = &nodes_[cur_node_++];

        //Node* r = new Node;
        memset(r, 0, sizeof(Node));
        r->left = r;
        r->right = r;
        r->up = r;
        r->down = r;
        r->name = col;
        r->col = columns_[col];
        put_up(r->col, r);
        return r;
    }

    int get_row_col(int row, int val)
    {
        return kRow+row*10+val;
    }

    int get_col_col(int col, int val)
    {
        return kCol+col*10+val;
    }

    int get_box_col(int box, int val)
    {
        return kBox+box*10+val;
    }

    Column* get_min_column()
    {
        Column* c = root_->right;
        int min_size = c->size;
        if (min_size > 1) {
            for (Column* cc = c->right; cc != root_; cc = cc->right) {
                if (min_size > cc->size) {
                    c = cc;
                    min_size = cc->size;
                    if (min_size <= 1)
                        break;
                }
            }
        }
        return c;
    }

    void cover(Column* c)
    {
        c->right->left = c->left;
        c->left->right = c->right;
        for (Node* row = c->down; row != c; row = row->down) {
            for (Node* j = row->right; j != row; j = j->right) {
                j->down->up = j->up;
                j->up->down = j->down;
                j->col->size--;
            }
        }
    }

    void uncover(Column* c)
    {
        for (Node* row = c->up; row != c; row = row->up) {
            for (Node* j = row->left; j != row; j = j->left) {
                j->col->size++;
                j->down->up = j;
                j->up->down = j;
            }
        }
        c->right->left = c;
        c->left->right = c;
    }

    void put_left(Column* old, Column* nnew)
    {
        nnew->left = old->left;
        nnew->right = old;
        old->left->right = nnew;
        old->left = nnew;
    }

    void put_up(Column* old, Node* nnew)
    {
        nnew->up = old->up;
        nnew->down = old;
        old->up->down = nnew;
        old->up = nnew;
        old->size++;
        nnew->col = old;
    }
};

string solveSudoku(const StringPiece& puzzle)
{
  assert(puzzle.size() == kCells);

  string result = kNoSolution;

  int board[kCells] = { 0 };
  bool valid = true;
  for (int i = 0; i < kCells; ++i)
  {
    board[i] = puzzle[i] - '0';
    valid = valid && (0 <= board[i] && board[i] <= 9);
  }

  if (valid)
  {
    SudokuSolver s(board);
    if (s.solve())
    {
      result.clear();
      result.resize(kCells);
      for (int i = 0; i < kCells; ++i)
      {
        result[i] = static_cast<char>(board[i] + '0');
      }
    }
  }
  return result;
}

（二）八数码

输入的数据为9个字符组成的字符串，当前空格用x表示。有解返回操作字符串 l(左)、r(右)、u(上)、d(下)即最少步数移动路径，无解返回“No solution”。

这里要讲一下，除了使用A*算法进行启发式搜索之外，判重使用康托展开，可以有效的节约空间和提升效率（仅使用int记录状态即可）。

八数码算法核心代码：

struct Node
{
    int maze[3][3];
    int fun_h,fun_g;
    int pos_x,pos_y;
    int Hash;
    bool operator<(const Node nt)const{
        return fun_h+fun_g>nt.fun_h+nt.fun_g;
    }

    bool check()
    {
        if(pos_x>=0 && pos_x<3 && pos_y>=0 && pos_y<3)
            return true;
        return false;
    }
};

const int MAXNUM=370000;
int HASH[9]={1,1,2,6,24,120,720,5040,40320};//0!~8!
int dest=46233;
int vis[MAXNUM];
int pre[MAXNUM];
int way[4][2]={{0,1},{0,-1},{1,0},{-1,0}};//4 ways

class EightSolver
{
    public:
        EightSolver(string s)
        {
            memset(vis,-1,sizeof(vis));
            memset(pre,-1,sizeof(pre));
            int k=0;
            for(int i=0;i<3;i++)
                for(int j=0;j<3;j++)
                {
                    if((s[k]<='9'&&s[k]>='0')||s[k]=='x')
                    {
                        if(s[k]=='x')
                        {
                            begNode.maze[i][j]=0;
                            begNode.pos_x=i;
                            begNode.pos_y=j;
                        }
                        else
                            begNode.maze[i][j]=s[k]-'0';
                    }

                    k++;
                }
            begNode.Hash=getHash(begNode);
            begNode.fun_g=0;
            begNode.fun_h=getH(begNode);
            vis[begNode.Hash]=1;

        }
        string getAns()
        {
            string ans="";
            int nxt=dest;
            while(pre[nxt]!=-1)
            {
                switch(vis[nxt])
                {
                    case 0:ans+='r';break;
                    case 1:ans+='l';break;
                    case 2:ans+='d';break;
                    case 3:ans+='u';break;
                }
                nxt=pre[nxt];
            }
            reverse(ans.begin(),ans.end());
            return ans;
        }
        bool isOK()
        {
            std::vector<int> v;
            for(int i=0;i<3;i++)
                for(int j=0;j<3;j++)
                    v.push_back(begNode.maze[i][j]);
            int sum=0;
            for(int i=0;i<9;i++)
                for(int j=i+1;j<9;j++)
                    if(v[j]&&v[i]&&v[i]>v[j])
                        sum++;
            return !(sum&1);

        }
        void aStar()
        {
            if(begNode.Hash==dest)
                return ;
            std::priority_queue<Node> que;
            que.push(begNode);
            while(!que.empty())
            {
                Node u=que.top();
                que.pop();
                for(int i=0;i<4;i++)
                {
                    Node v=u;
                    v.pos_x+=way[i][0];
                    v.pos_y+=way[i][1];
                    if(v.check())
                    {
                        std::swap(v.maze[v.pos_x][v.pos_y],v.maze[u.pos_x][u.pos_y]);
                        v.Hash=getHash(v);
                        if(vis[v.Hash]==-1)
                        {
                            vis[v.Hash]=i;
                            v.fun_g++;
                            pre[v.Hash]=u.Hash;
                            v.fun_h=getH(v);
                            que.push(v);
                        }
                        if(v.Hash==dest)
                            return ;
                    }
                }
            }

        }
    private:
        Node begNode;
        int getHash(Node &tmp)
        {
            std::vector<int> v;
            for(int i=0;i<3;i++)
                for(int j=0;j<3;j++)
                    v.push_back(tmp.maze[i][j]);
            int res=0;
            for(int i=0;i<9;i++)
            {
                int k=0;
                for(int j=i+1;j<9;j++)
                    if(v[j]<v[i])
                        k++;
                res+=HASH[8-i]*k;
            }
            return res;
        }


        int getH(Node &tmp)
        {
            int ans=0;
            for(int i=0;i<3;i++)
                for(int j=0;j<3;j++)
                    if(tmp.maze[i][j])
                        ans+=abs(i-(tmp.maze[i][j]-1)/3)+abs(j-(tmp.maze[i][j]-1)%3);
            return ans;
        }
};


string solveEight(const StringPiece& puzzle)
{
    string board="";
    string constStr="No solution";
    for(int i=0;i<puzzle.size();i++)
    {
        board+=puzzle[i];
    }
    EightSolver s(board);
    if(!s.isOK())
        return constStr;
    else
    {
       s.aStar();
       return s.getAns();
    }

}

最后，这两个服务是融合的，开启服务器后，使用telnet命令访问，满足要求的字符串便会自动分类解析返回结果，效果图如下（Linux下）：

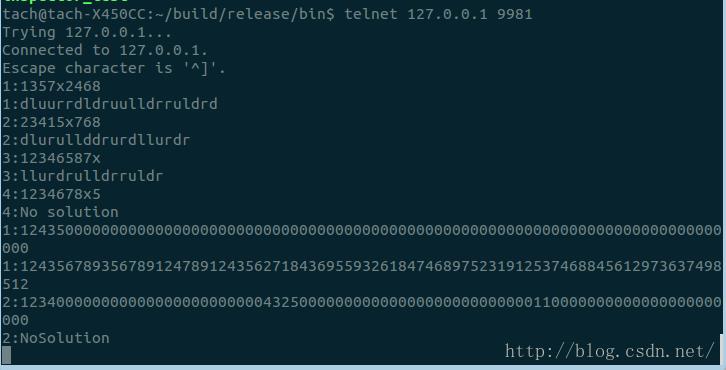
由于是基于muduo网络库实现的，所以可以很轻松的实现高效可靠的并发访问~。

项目全部源码托管于 Github （https://github.com/Tachone/sukuEight），有兴趣的读者可以继续完善，同时强烈欢迎前端的同学做一些web界面，让这个求解程序更加人性化~