数据结构树之初体验

Posted 2020-07-16

引言

在线性表中，元素之间的逻辑关系是平等（peer）的，没有等级之分，只有先后之分。但是在树中，元素之间是由复杂的族谱关系构成的。

 

树的定义

n个元素按照倒置的树的形态构成的一个集合。每一个元素对应树中的一个结点

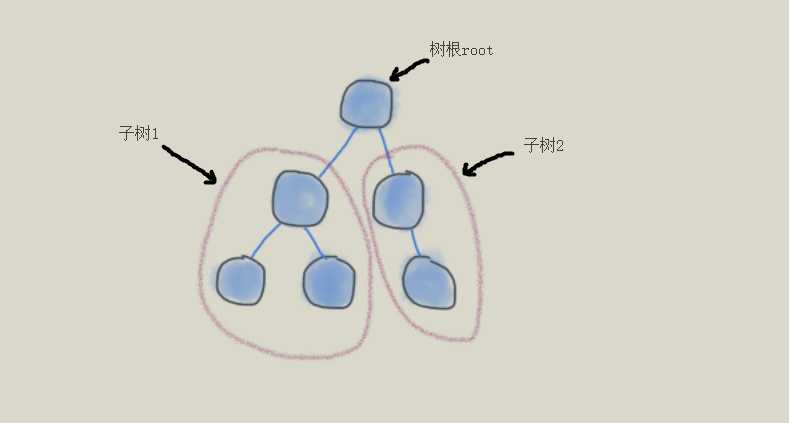
(1)树根：一颗树中，有且仅有一个特定的称为根(Root)的结点；
(2)其余的结点可分为m(m≥0)个互不相交的子集T_l，T₂，…，T_m，其中每个子集本身又是一棵树，并称其为根的子树(Subree)。

可见，树的定义是一个递归的定义。

 

 

          

 

 

 

 

 与树相关的名词的解释

与树相关的概念很多，但是理解了 ，看起来就会觉得很有道理。记下还是好的，不然看其他文献，你不知道别人在说什么，而且考试最喜欢这个了- -。

 

空树            ：一个结点也没有的树。

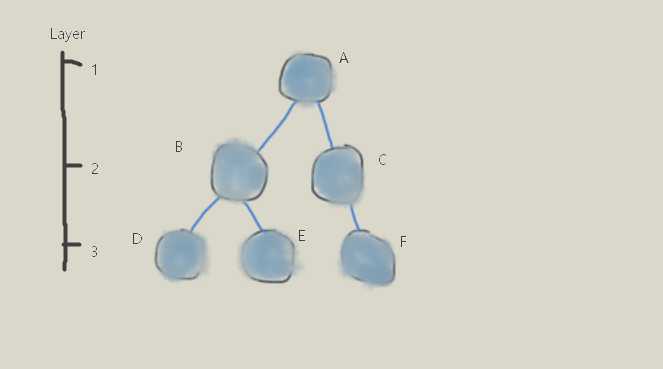
树的深度      ：树的层次。下图中，树的深度为3

数的度         ：树中所有结点度的最大值。下图中，A的度为2，B的度也为2，其他都是1，so，这个树的度为2.

有序树         ：子树之间是有序的，是在意顺序的。

无序树         ：子数之间相互交换位置不影响，不在意顺序。

 

叶子结点          ：终端结点，没有子结点的结点。下图中，D,E,F都是叶子结点。

分支结点          ：非终端结点。有子结点的结点。下图中，A,B,C都是分支结点。

结点的度          ：一个结点拥有的子结点的个数（孩子的个数）。下图中，B有2个子结点，则它的度为2.

孩子结点          ：一个结点的直接子结点，叫做这个结点的孩子结点。下图中，A的孩子为B，C。F是C的孩纸。

双亲（父结点）  ：一个结点的父结点。除了root结点外，一个结点仅有一个双亲。下图中，A是B和C共同的父节点。

兄弟                ：拥有同一个父结点的结点之间互为兄弟。下图中，B和C是兄弟，D和E是兄弟。

堂兄弟             ：同一层的结点之间互为堂兄弟。下图中，D,E和F互为堂兄弟。

子孙                ： 从一个结点派生出来的所有结点，都叫这个结点的子孙，包括它的孩子。下图中，B,C,E,D,F都是A的子孙。

 

 

                  

 

 

 

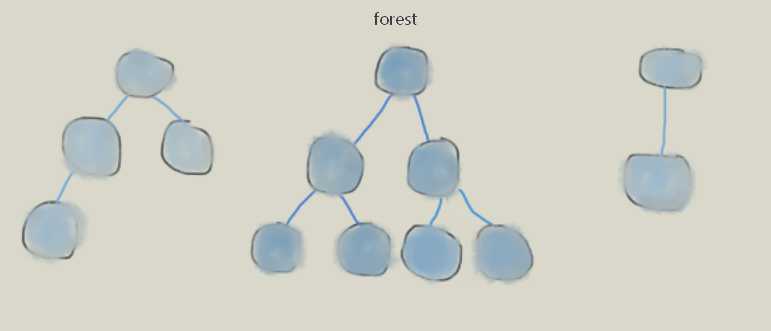
             森林： m个互不相关的树，构造森林。

       

                 

 

 

 二叉树

 二叉树的度为2，也就是说，每一个结点的孩子最多有2个，并且，这2个孩纸是有左右之分的。即便是只有1个孩子，也分为左孩子，或右孩子。

 

二叉树的性质

 

1、二叉树的第i层上的节点数最多为 2^i-1 个 （i>=1）

    达到最多时，是按照满二叉树来考虑的。

 

2、 深度为k的二叉树至多有2^k-1个结点(k≥1)。

      根据性质1，可以得出：total_node = 2⁰ + 2¹ + 2² + .....+ 2^k-1

 

      可以发现，这是一个公比为2的k项 等比数列，由等比公式求和得到total_node = 2^K - 1

     

 

3、在任意一棵二叉树中，若终端（叶子）结点的个数为n0，度为2的结点数为n2，则有：n0=n2+1。

    要证明这个性质，就要从点和线的方面去分析。

    设：度为2的结点个数有n2个，度为1的结点有n1个，度为0  的叶子结点有n0个，树的总结点为total个。

         树的总的 连线 的个数为L条。

        

        ①  total = n2 + n1 + n0

        ②  L = total - 1                      除了root结点，其他结点都是由头顶上的一条线引出来的。

        ③  L = 2*n2 + n1                   度为2的结点，必顶会向下引出2条线， 同理，度为1的结点会引出1条。

 

      结合3个式子消元得：n0 = n2 + 1

 

 

 

 

 

 

 

  满二叉树

  除了叶子结点外，每一个结点的度都达到最大值2。

         

             

   

 

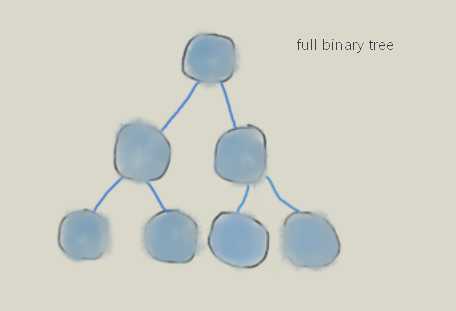
 完全二叉树

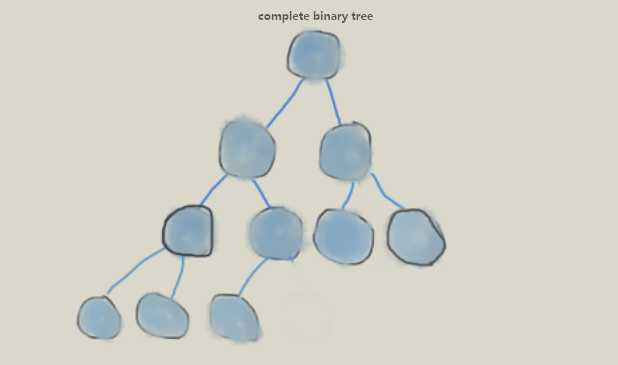
 若一棵二叉树至多只有最下面的两层上结点的度数可以小于2，并且最下一层上的结点都集中在该层最左边的若干位置上，则此二叉树称为完全二叉树。

 例如：在K层满二叉树的基础上，删去最下层，最右边的连续的n(n>=0)个叶子结点，即可得到一个K层完全二叉树。

 特点：满二叉树一定是一个完全二叉树，反过来则不一定。

 

性质：

 

1、有n个结点的完全二叉树的深度为：int(log₂ⁿ) + 1

 

 int(log₂ⁿ) 表示 不大于 log₂ⁿ 的最大整数。

 

             

 

 

 

 

 

链式二叉树

 和线性表一样，二叉树也有顺序实现和链式实现，为了简单起见，我们将精力集中在3种遍历算法上，所以选择了链式实现。顺序实现后面再提。

 

 首先我们构建数据类型，假设存储的目标数据类型为char。

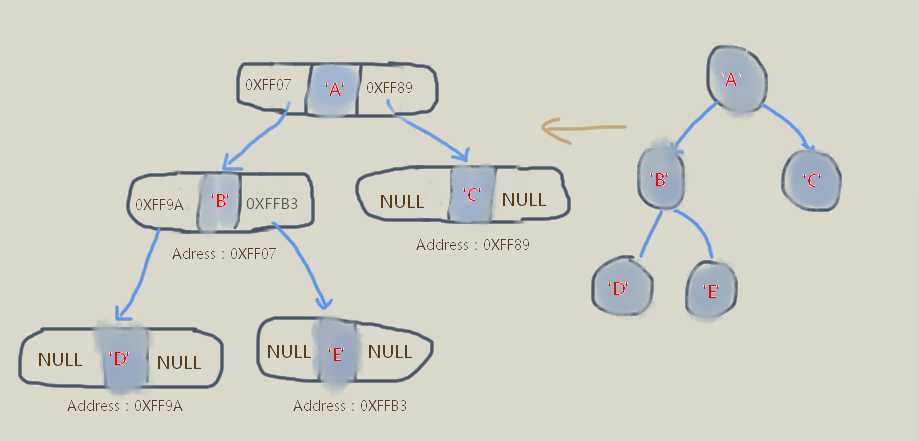
 下面是一个5个元素的二叉树例子。结点的data分别为字符 A  ,B  ,C  ,E , F。每个结点除了含有data域，还有2个指针域，分别保存它的2个孩子的内存地址。

  结点的地址是我假定的，目的上说明他们之间的关系。

 

     

 

 

 

typedef char DataType;       //目标储存对象类型

typedef struct node          //结点
{
    DataType data;
    struct node*left;     
    struct node*right;

}Node;

typedef Node* LinkedBinaryTree;

 

通过手动硬编码的方式创建这个树，当然这个不是个好方法。然而我们在这里只想将精力放在理解3中遍历算法上，所以，这里就忍忍吧。相信理解了遍历，其他问题就会迎刃而解。

 

完整代码

#include<stdio.h>


typedef char DataType;

typedef struct node
{
    DataType data;
    struct node*left;
    struct node*right;

}Node;

typedef Node* LinkedBinaryTree; 

/***************function declare*******************/
void LinkedBinaryTree_init(LinkedBinaryTree *ptree);


int main()
{
    
    LinkedBinaryTree tree;
    
    LinkedBinaryTree_init(&tree);
    
    
    
    
    return 0;
}


void LinkedBinaryTree_init(LinkedBinaryTree *ptree)
{
    //root
    *ptree = new Node;     
    (*ptree)->data = ‘A‘;

    //b
    Node*pb = new Node;
    pb->data = ‘B‘;


    //c
    Node*pc = new Node;
    pc->data = ‘C‘;


    //d
    Node*pd = new Node;
    pd->data = ‘D‘;

    //e
    Node*pe = new Node;
    pe->data = ‘E‘;


    //链接
    (*ptree)->left = pb; (*ptree)->right = pc;

    pb->left = pd;   pb->right = pe;  pc->left = NULL; pc->right = NULL;
    
    pd->left = NULL; pd->right = NULL; pe->left = NULL; pe->right = NULL;

}

View Code

 

 

至此，我们已近创建好了树。好了，先歇息歇息，下一站：二叉树的遍历