第3节二叉树的基本操作（非递归实现）

Posted 2020-07-15 法海你懂不

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第3节二叉树的基本操作（非递归实现）相关的知识，希望对你有一定的参考价值。

二叉树的非递归遍历

上一节二叉树的递归遍历中简单介绍了二叉树的递归遍历的实现方式，本节主要介绍二叉树的非递归遍历实现，继续引用上节的例子来说明下。

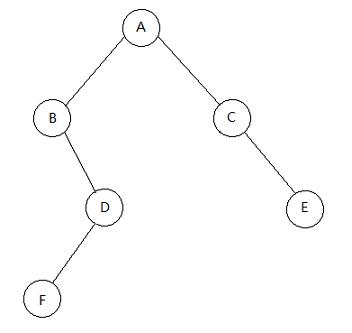
Order

一.先序遍历

二叉树先序遍历的访问顺序为：根结点->左孩子->右孩子。简单的说，对于任意一个结点，均可以看作是根结点，直接对其访问，如果访问完成后，左孩子不为空，则可以将该左孩子再次看成一个新的根结点，那么就又回到开始，访问根结点，访问左孩子，如果左孩子为空时，访问它的右孩子。对于一般程序而言，递归程序转为非递归程序需要引入栈这个数据结构，可以参考第2章第1节栈的基本定义以及实现方式，其处理过程可以简单分为三步：

对于任一结点T：

访问结点T，并将结点T入栈;
判断结点T的左孩子是否为空，若不为空，则将结点T的左孩子入栈；再判断T的右孩子是否为空，若不为空，则将结点T的右孩子入栈；若为左孩子或右孩子为空，则出栈访问。这里应该注意到栈的先进后出的特性，因此需要先将右孩子入栈，再将左孩子入栈；
最后直到栈为空便结束访问。

算法描述如下：

void PreOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode* p=T;
    Push(&S,p);
    while(IsEmptyStack(&S)!=0){
        p=Pop(&S);
        printf("%c",p->data);
        if(p->rchild!=NULL){
            Push(&S,p->rchild);
        }
        if(p->lchild!=NULL){
            Push(&S,p->lchild);
        }
    }
}

二.中序遍历

二叉树中序遍历的访问顺序为左孩子->根结点->右孩子。简单来说就是：先扫描（不访问）根结点的所有左孩子并将它们一一入栈，然后出栈一个结点*p并且访问它，然后扫描该结点*p的右孩子，并将其入栈，再扫描以该结点*p的右孩子为根结点的所有左孩子，并将其一一入栈，如此继续，直到栈为空为止。其处理过程可以简单分为三步：

对于任一结点T：

首先判断结点T是否为空，若不为空，则将其入栈，然后让指针p指向结点T的左孩子；接着继续重复该步骤，直到结点T为空为止；
经过第一步可以保证栈顶元素一定是该二叉树最左的孩子结点，然后出栈访问该结点，接着判断其右孩子是否为空，若不为空，接着扫描右孩子的左孩子结点，重复第1步；
最后直到栈为空时便结束访问。

算法描述如下：

void InOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode* p=T;

    while(p||IsEmptyStack(&S)!=0){
        if(p!=NULL){
            Push(&S,p);
            p=p->lchild;
        }else{
            p=Pop(&S);
            printf("%c",p->data);
            p=p->rchild;
        }
    }
}

三. 后序遍历

二叉树中序遍历的访问顺序为左孩子->右孩子->根结点。因为后序非递归遍历二叉树的顺序是先访问左孩子，再访问右孩子，最后访问根结点。所以当用栈来存储结点时，必须分清返回根结点时是从左孩子返回的还是从右孩子返回的，需要设置一个辅助指针r，让其指向最近访问过的结点。其处理过程可以简单分为三步：

对于任一结点T：

首先判断根结点是否为空，若不为空，则不断的入栈直到最左边的左孩子结点为止；
接着取出栈顶结点，判断其右孩子是否为空，而且其右孩子没有被访问过，接着对其右孩子入栈，再重复第1，2步；
但是若右孩子为空，则出栈访问，并对该结点标记。

算法描述如下：

void PostOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode *p=T;
    BiTNode *r=NULL;

    while(p||IsEmptyStack(&S)!=0){
        if(p!=NULL){
            Push(&S,p);
            p=p->lchild;
        }else{
            p=GetTop(&S);
            if(p->rchild!=NULL&&p->rchild!=r){
                p=p->rchild;
                Push(&S,p);
                p=p->lchild;
            }else{
                p=Pop(&S);
                printf("%c",p->data);
                r=p;
                p=NULL;
            }
        }
    }
}

四.层次遍历

一般的二叉树层次遍历是自上而下，自左向右。简单来说就是先访问根结点，然后访问其左孩子，右孩子，可以借助队列的特性先进先出来实现层次遍历，可以参考第2章第2节队列的基本定义以及实现方式，其处理过程可以简单分为三步：

对于任一结点T：

访问结点T，然后将结点T入队；
出队访问该结点，然后判断其左孩子和右孩子是否为空，如果不为空，则分别将其入队；
若为空，出队访问便可；

void PostOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode *p=T;
    BiTNode *r=NULL;

    while(p||IsEmptyStack(&S)!=0){
        if(p!=NULL){
            Push(&S,p);
            p=p->lchild;
        }else{
            p=GetTop(&S);
            if(p->rchild!=NULL&&p->rchild!=r){
                p=p->rchild;
                Push(&S,p);
                p=p->lchild;
            }else{
                p=Pop(&S);
                printf("%c",p->data);
                r=p;
                p=NULL;
            }
        }
    }
}

具体代码见附件

附件

//AB#DF###C#E##
#include<stdio.h>
#include<stdlib.h>

#define MaxSize 100
typedef char ElemType;

/*-----------------------------------------*/

typedef struct BiTNode{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

BiTNode* CreateBiTree(BiTNode*);
void PreOrder(BiTNode*);
void InOrder(BiTNode*);
void PostOrder(BiTNode*);
void LevelOrder(BiTNode*);

/*-----------------------------------------*/

typedef struct SqStack{
    BiTNode* data[MaxSize];
    int top;
}SqStack;

void InitStack(SqStack*);
void Push(SqStack*,BiTNode*);
BiTNode* Pop(SqStack*);
BiTNode* GetTop(SqStack*);
int IsEmptyStack(SqStack*);

typedef struct SqQueue{
    BiTNode* data[MaxSize];
    int front, rear;
}SqQueue;

void InitQueue(SqQueue*);
void EnQueue(SqQueue*, BiTNode*);
BiTNode* DeQueue(SqQueue*);
int IsEmptyQueue(SqQueue*);

/*-----------------------------------------*/

int main(int argc, char* argv[]){
    BiTNode *T=(BiTNode*)malloc(sizeof(BiTNode));
    T=CreateBiTree(T);
    PreOrder(T);printf("\\n");
    InOrder(T);printf("\\n");
    PostOrder(T);printf("\\n");
    LevelOrder(T);printf("\\n");
    return 0;
}

//创建二叉树
BiTree CreateBiTree(BiTNode* T){
    ElemType x;
    scanf("%c",&x);
    if(x=='#'){
        return T;
    }else{
        T=(BiTNode*)malloc(sizeof(BiTNode));
        T->data=x;
        T->lchild=CreateBiTree(T->lchild);
        T->rchild=CreateBiTree(T->rchild);
    }
    return T;
}

//先序遍历
void PreOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode* p=T;
    Push(&S,p);
    while(IsEmptyStack(&S)!=0){
        p=Pop(&S);
        printf("%c",p->data);
        if(p->rchild!=NULL){
            Push(&S,p->rchild);
        }
        if(p->lchild!=NULL){
            Push(&S,p->lchild);
        }
    }
}

//中序遍历
void InOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode* p=T;

    while(p||IsEmptyStack(&S)!=0){
        if(p!=NULL){
            Push(&S,p);
            p=p->lchild;
        }else{
            p=Pop(&S);
            printf("%c",p->data);
            p=p->rchild;
        }
    }
}

//后序遍历
void PostOrder(BiTNode* T){
    SqStack S;
    InitStack(&S);

    BiTNode *p=T;
    BiTNode *r=NULL;

    while(p||IsEmptyStack(&S)!=0){
        if(p!=NULL){
            Push(&S,p);
            p=p->lchild;
        }else{
            p=GetTop(&S);
            if(p->rchild!=NULL&&p->rchild!=r){
                p=p->rchild;
                Push(&S,p);
                p=p->lchild;
            }else{
                p=Pop(&S);
                printf("%c",p->data);
                r=p;
                p=NULL;
            }
        }
    }
}

//层次遍历
void LevelOrder(BiTNode* T){
    SqQueue Q;
    InitQueue(&Q);

    BiTNode *p=T;
    EnQueue(&Q,p);

    while(IsEmptyQueue(&Q)!=0){
        p=DeQueue(&Q);
        printf("%c",p->data);
        if(p->lchild!=NULL){
            EnQueue(&Q,p->lchild);
        }
        if(p->rchild!=NULL){
            EnQueue(&Q,p->rchild);
        }
    }
}

/*-----------------------------------------*/

void InitStack(SqStack* S){
    S->top=-1;
}

void Push(SqStack* S, BiTNode* T){
    if(S->top==MaxSize-1){
        return;
    }
    S->data[++S->top]=T;
}

BiTNode* Pop(SqStack* S){
    if(S->top==-1){
        return NULL;
    }
    return S->data[S->top--];

}

BiTNode* GetTop(SqStack* S){
    if(S->top==-1){
        return NULL;
    }
    return S->data[S->top];
}

int IsEmptyStack(SqStack* S){
    if(S->top==-1){
        return 0;
    }
    return -1;
}

/*-----------------------------------------*/

void InitQueue(SqQueue* Q){
    Q->front=0;
    Q->rear=0;
}

void EnQueue(SqQueue* Q, BiTNode* T){
    if((Q->rear+1)%MaxSize==Q->front){
        return;
    }
    Q->data[Q->rear++]=T;
}

BiTNode* DeQueue(SqQueue* Q){
    if(Q->front==Q->rear){
        return NULL;
    }
    return Q->data[Q->front++];
}

int IsEmptyQueue(SqQueue* Q){
    if(Q->front==Q->rear){
        return 0;
    }
    return -1;
}

以上是关于第3节二叉树的基本操作（非递归实现）的主要内容，如果未能解决你的问题，请参考以下文章

第2节二叉树的基本操作（递归实现）

第四章第4节二叉树特殊节点个数统计

Java二叉树的递归，非递归遍历，高度，节点数，叶子节点数

二叉树的遍历--递归实现与非递归实现

Java实现二叉树的创建递归/非递归遍历

二叉树的镜像(反转二叉树)

第3节 二叉树的基本操作（非递归实现）

二叉树的非递归遍历

一.先序遍历

二.中序遍历

三. 后序遍历

四.层次遍历

附件

第3节二叉树的基本操作（非递归实现）