稀疏矩阵

Posted 2020-11-30 guoyujiang

SparseMatrix

存储：

使用三元表存储，即结构体数组

struct element
{
　　int row, col;//元素item在矩阵中的位置
　　T item;
};

矩阵转置方法：A->B（A按行存储，要求转置得到的矩阵按列存储）

1、直接取，顺序存

　　从左到右，上到下进行存储

2、顺序取，直接存

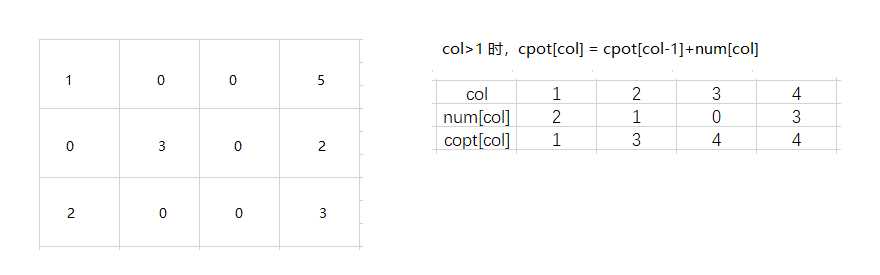
　　计算每一列的元素数目和每一列非零元素的位置上

1 for (i = 0; i<A.tu; i++) //遍历A的所有元素
2         {
3             j = A.data[i].col;//三元表A的元素i的列号
4             k = cpot[j];//k为待存元素在B中的位置
5             B.data[k].row = A.data[i].col;
6             B.data[k].col = A.data[i].row;
7             B.data[k].item = A.data[i].item;
8             cpot[j]++;//A中记录在cpot中的每一列非零元素改变
9         }

以列号j=4做示范：

　　当一个元素的列满足要求时，得到k = cpot[j], k为B的三元表中待存位置，然后cpot[j]++，使下一个同列元素存在其下

 

 

 

 

  1 //稀疏矩阵
  2 #include <iostream>
  3 
  4 using namespace std;
  5 const int MAXTERM = 100;//三元表最长长度
  6 
  7 template<class T>
  8 struct element
  9 {
 10     int row, col;//元素item在矩阵中的位置
 11     T item;
 12 };
 13 
 14 template<class T>
 15 class SparseMatrix
 16 {
 17 public:
 18     SparseMatrix() {}
 19     //有参数的构造函数
 20     SparseMatrix(int intmu, int intnu, int inttu, element<T> datatemp[]);
 21     ~SparseMatrix() {}//释放空间
 22     element<T> GetMatrix(int intnumber);//输出对应下标下的数组元素【索引值】
 23     void Prt();//打印三元组顺序表
 24     void Trans1(SparseMatrix<T> &B);//矩阵的转置，直接取，顺序存
 25     void Trans2(SparseMatrix<T> A, SparseMatrix<T> &B);//矩阵的转置，顺序取，直接存
 26 private:
 27     element<T>data[MAXTERM];
 28     int mu, nu, tu;//矩阵的行，列，不同元素个数
 29 };
 30 
 31 int _tmain(int argc, _TCHAR* argv[])
 32 {
 33     try {
 34         element<int> elementtemp1, elementtemp2, elementtemp3;
 35         elementtemp1.col = 0, elementtemp1.row = 0, elementtemp1.item = 15;
 36         elementtemp2.col = 1, elementtemp2.row = 2, elementtemp2.item = 16;
 37         elementtemp3.col = 1, elementtemp3.row = 0, elementtemp3.item = 17;
 38         //(0,0),(0,1),(2,1)
 39         element<int> A[3];
 40         A[0] = elementtemp1, A[1] = elementtemp2, A[2] = elementtemp3;
 41 
 42         SparseMatrix<int> sparsematrixB;
 43         SparseMatrix<int> sparsematrixA(3, 3, 3, A);
 44 
 45         cout << "源三元组顺序表如下：" << endl;
 46         sparsematrixA.Prt();
 47         sparsematrixA.Trans1(sparsematrixB);
 48         cout << "使用直接取、顺序存转置算法转置后的三元组顺序表如下：" << endl;
 49         sparsematrixB.Prt();
 50         sparsematrixA.Trans2(sparsematrixA, sparsematrixB);
 51         cout << "使用顺序取、直接存转置算法后的三元组顺序表如下：" << endl;
 52         sparsematrixB.Prt();
 53     }
 54     catch (char *s)
 55     {
 56         cout << s << endl;
 57     }
 58     system("pause");
 59     return 0;
 60 }
 61 
 62 template<class T>
 63 SparseMatrix<T>::SparseMatrix(int intmu, int intnu, int inttu, element<T> datatemp[])
 64 {
 65     if (inttu>MAXTERM)
 66         throw"构造函数的初始化参数不正确";
 67     mu = intmu, nu = intnu, tu = inttu;
 68     for (int i = 0; i<inttu; i++)
 69         data[i] = datatemp[i];
 70 }
 71 
 72 template<class T>
 73 element<T> SparseMatrix<T>::GetMatrix(int intnumber)
 74 {
 75     if (intnumber<0 || intnumber >= tu)
 76         throw"输入位置不正确";
 77     return data[i];
 78 }
 79 
 80 template<class T>
 81 void SparseMatrix<T>::Prt()
 82 {
 83     for (int i = 0; i<tu; i++)
 84         cout << "row:" << data[i].row << ",col:" << data[i].col << ",item:" << data[i].item << endl;
 85 }
 86 
 87 
 88 
 89 template<class T>//待转置的源三元组顺序表A和目标三元顺序表B的引用
 90 void SparseMatrix<T>::Trans1(SparseMatrix<T> &B)
 91 {
 92     int pb;
 93     B.mu = nu, B.nu = mu, B.tu = tu;
 94 
 95     if (B.tu>0)
 96     {
 97         pb = 0;
 98         for (int col = 0; col < nu; col++)
 99             for (int i = 0; i < tu; i++)
100                 if (data[i].col == col)
101                 {
102                     B.data[pb].row = data[i].col;
103                     B.data[pb].col = data[i].row;
104                     B.data[pb++].item = data[i].item;
105                 }
106     }
107 }
108 
109 template<class T>
110 void SparseMatrix<T>::Trans2(SparseMatrix<T> A, SparseMatrix<T> &B)
111 {
112     B.mu = A.nu, B.nu = A.mu, B.tu = A.tu;
113     int i, j, k, num[MAXTERM], cpot[MAXTERM];
114     if (B.tu > 0)
115     {
116         for (i = 0; i<A.nu; i++)
117             num[i] = 0;//A中每一列的非零个数，初始化为0
118         for (i = 0; i<A.tu; i++)
119         {
120             j = A.data[i].col;
121             num[j]++;//得到A每一列的元素数，得到num[i]
122         }
123         cpot[0] = 0;//A中第0列中第一个元素在B的三元表中位置为0
124         for (i = 1; i<A.nu; i++)
125             cpot[i] = cpot[i - 1] + num[i - 1];//求A中第i列第一个非零元素在B的三元表中的下标
126 
127         for (i = 0; i<A.tu; i++)
128         {
129             j = A.data[i].col;//三元组元素i的列号
130             k = cpot[j];//A中第j列的非零元素的下标【行号】
131             B.data[k].row = A.data[i].col;
132             B.data[k].col = A.data[i].row;
133             B.data[k].item = A.data[i].item;
134             cpot[j]++;//A中第j列的非零元素下标【行号】下移
135         }
136     }
137 }

View Code