模板高精算法
Posted maoyiting
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模板高精算法相关的知识,希望对你有一定的参考价值。
利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。介绍常用的几种高精度计算的方法。
高精度计算中需要处理好以下几个问题:
1)数据的接收方法和存贮方法
数据的接收和存贮:当输入的数很长时,可采用字符串方式输入,这样可输入数字很长的数,利用字符串函数和操作运算,将每一位数取出,存入数组中。另一种方法是直接用循环加数组方法输入数据。
void init(int a[]) //传入一个数组 { string s; cin>>s; //读入字符串s len=s.length(); //用len计算字符串s的位数 for(i=1;i<=len;i++) a[i]=s[len-i] -‘0‘; //将数串s转换为数组a,并倒序存储 }//另一种方法是直接用循环加数组方法输入数据。
(2) 高精度数位数的确定
位数的确定:接收时往往是用字符串的,所以它的位数就等于字符串的长度。
(3) 进位,借位处理
加法进位:
c[i]=a[i]+b[i]; if(c[i]>=10) c[i]%=10,++c[i+1];
减法借位:
if(a[i]<b[i]) --a[i+1],a[i]+=10; c[i]=a[i]-b[i];
乘法进位:
c[i+j-1]= a[i]*b[j] + x + c[i+j-1]; x=c[i+j-1]/10,c[i+j-1] %= 10;
(4) 商和余数的求法
商和余数处理:视被除数和除数的位数情况进行处理.
【例1】高精度加法。输入两个正整数,求它们的和。
【分析】
输入两个数到两个变量中,然后用赋值语句求它们的和,输出。但是,我们知道,在C++语言中任何数据类型都有一定的表示范围。而当两个被加数很大时,上述算法显然不能求出精确解,因此我们需要寻求另外一种方法。在读小学时,我们做加法都采用竖式方法,如图1。 这样,我们方便写出两个整数相加的算法。
如果我们用数组A、B分别存储加数和被加数,用数组C存储结果。则上例有A[1]=6,A[2]=5, A[3]=8,B[1]=5,B[2]=5,B[3]=2,C[4]=1,C[3]=1,C[2]=1,C[1]=1,两数相加如图2所示。
//因此,算法描述如下: int c[100]; void add(int a[],int b[]) //a,b,c都为数组,分别存储被加数、加数、结果 { int i=1,x=0; //x是进位 while ((i<=a数组长度)||(i<=b数组的长度)){ c[i]=a[i]+b[i]+x; //第i位相加并加上次的进位 x=c[i]/10; //向高位进位 c[i]%=10; //存储第i位的值 i++; //位置下标变量 } }
参考代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1000000+5; 4 long long a[N],b[N],c[N],base=10; 5 char tmp[N]; 6 int main() 7 { 8 cin>>tmp; 9 int n=strlen(tmp); 10 for(int i=0;i<n;i++) 11 a[i]=tmp[n-i-1]-‘0‘; 12 cin>>tmp; 13 int m=strlen(tmp); 14 for(int i=0;i<m;i++) 15 b[i]=tmp[m-i-1]-‘0‘; 16 memset(c,0,sizeof(c)); 17 int up=max(n,m); 18 for(int i=0;i<up;i++) 19 { 20 c[i]+=a[i]+b[i]; 21 c[i+1]+=c[i]/base; 22 c[i]=c[i]%base; 23 } 24 if(c[up]) up++; 25 for(int i=up-1;i>=0;i--) printf("%d",c[i]); 26 puts(""); 27 return 0; 28 }
【例2】高精度减法。输入两个正整数,求它们的差。
【算法分析】
类似加法,可以用竖式求减法。在做减法运算时,需要注意的是:被减数必须比减数大,同时需要处理借位。高精度减法的参考程序:
大数减小数做法:
1 //大数减小数 2 #include<bits/stdc++.h> 3 using namespace std; 4 const int N=100000+5; 5 int a[N],b[N],c[N],base=10; 6 char tmp[N]; 7 int main() 8 { 9 cin>>tmp; 10 int n=strlen(tmp); 11 for(int i=0;i<n;i++) 12 a[i]=tmp[n-i-1]-‘0‘; 13 cin>>tmp; 14 int m=strlen(tmp); 15 for(int i=0;i<m;i++) 16 b[i]=tmp[m-i-1]-‘0‘; 17 memset(c,0,sizeof(c)); 18 int up=max(n,m); 19 for(int i=0;i<up;i++) 20 { 21 c[i]=a[i]-b[i]; 22 if(c[i]<0) c[i+1]--,c[i]+=base; 23 } 24 while(!c[up-1]&&up>1) up--; 25 for(int i=up-1;i>=0;i--) printf("%d",c[i]); 26 puts(""); 27 return 0; 28 }
大数减大数
1 //大数减大数 2 #include<bits/stdc++.h> 3 using namespace std; 4 long long a[100010],b[100010],c[100010],lena,lenb,lenc,i; 5 char n[100010],n1[100010],n2[100010]; 6 int main() 7 { 8 memset(a,0,sizeof(a)); 9 memset(b,0,sizeof(b)); 10 memset(c,0,sizeof(c)); 11 cin>>n1; 12 cin>>n2; 13 if(strlen(n1)<strlen(n2)||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0)) 14 { 15 strcpy(n,n1); 16 strcpy(n1,n2); 17 strcpy(n2,n); 18 cout<<"-"; 19 } 20 lena=strlen(n1); 21 lenb=strlen(n2); 22 for(i=0;i<=lena-1;i++) 23 a[lena-i]=int(n1[i]-‘0‘); 24 for(i=0;i<=lenb-1;i++) 25 b[lenb-i]=int(n2[i]-‘0‘); 26 i=1; 27 while(i<=lena||i<=lenb) 28 { 29 if(a[i]<b[i]) a[i]+=10,a[i+1]--; 30 c[i]=a[i]-b[i]; 31 i++; 32 } 33 lenc=i; 34 while((c[lenc]==0)&&(lenc>1)) lenc--; 35 for(i=lenc;i>=1;i--) 36 cout<<c[i]; 37 cout<<endl; 38 return 0; 39 }
【例3】高精度乘法。输入两个正整数,求它们的积。
【算法分析】
类似加法,可以用竖式求乘法。在做乘法运算时,同样也有进位,同时对每一位进行乘法运算时,必须进行错位相加,如图3、图4。
分析c数组下标的变化规律,可以写出如下关系式:ci = c’i +c”i +…由此可见,c i跟a[i]*b[j]乘积有关,跟上次的进位有关,还跟原c i的值有关,分析下标规律,有c[i+j-1]= a[i]*b[j]+ x + c[i+j-1]; x=c[i+j-1]/10 ; c[i+j-1]%=10;
参考代码
高精乘低精
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=100000+5; 4 int a[N],b,c[N],base=10; 5 char tmp[N]; 6 int main() 7 { 8 gets(tmp); 9 int n=strlen(tmp); 10 for(int i=0;i<n;i++) 11 a[i]=tmp[n-i-1]-‘0‘; 12 int b; 13 scanf("%d",&b); 14 memset(c,0,sizeof(c)); 15 int up=n; 16 for(int i=0;i<up;i++) 17 { 18 c[i]+=a[i]*b; 19 c[i+1]+=c[i]/base; 20 c[i]=c[i]%base; 21 } 22 if(c[up]) up++; 23 while(c[up]>base) c[up+1]+=c[up]%base,c[up]=c[up]%base,up++; 24 for(int i=up-1;i>=0;i--) printf("%d",c[i]); 25 puts(""); 26 return 0; 27 }
高精乘高精
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=100000+5; 4 int a[N],b[N],c[N],base=10; 5 char tmp[N]; 6 int main() 7 { 8 cin>>tmp; 9 int n=strlen(tmp); 10 for(int i=0;i<n;i++) 11 a[i]=tmp[n-i-1]-‘0‘; 12 cin>>tmp; 13 int m=strlen(tmp); 14 for(int i=0;i<m;i++) 15 b[i]=tmp[m-i-1]-‘0‘; 16 memset(c,0,sizeof(c)); 17 for(int i=0;i<n;i++) 18 for(int j=0;j<m;j++) 19 c[i+j]+=a[i]*b[j]; 20 int up=n+m-1; 21 for(int i=0;i<up;i++) 22 { 23 c[i+1]+=c[i]/base; 24 c[i]=c[i]%base; 25 } 26 if(c[up]) up++; 27 if(c[up-1]==0){cout<<0<<endl;return 0;} 28 for(int i=up-1;i>=0;i--) printf("%d",c[i]); 29 puts(""); 30 return 0; 31 }
利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。介绍常用的几种高精度计算的方法。
高精度计算中需要处理好以下几个问题: ### 1)数据的接收方法和存贮方法数据的接收和存贮:当输入的数很长时,可采用字符串方式输入,这样可输入数字很长的数,利用字符串函数和操作运算,将每一位数取出,存入数组中。另一种方法是直接用循环加数组方法输入数据。
```cppvoid init(int a[]) //传入一个数组{string s; cin>>s; //读入字符串s len=s.length(); //用len计算字符串s的位数 for(i=1;i<=len;i++) a[i]=s[len-i] -‘0’; //将数串s转换为数组a,并倒序存储 }//另一种方法是直接用循环加数组方法输入数据。```
### (2) 高精度数位数的确定位数的确定:接收时往往是用字符串的,所以它的位数就等于字符串的长度。
### (3) 进位,借位处理加法进位:```cppc[i]=a[i]+b[i];if (c[i]>=10) c[i]%=10,++c[i+1];```
减法借位:```cppif (a[i]<b[i]) --a[i+1],a[i]+=10; c[i]=a[i]-b[i];```
乘法进位:```cppc[i+j-1]= a[i]*b[j] + x + c[i+j-1];x=c[i+j-1]/10,c[i+j-1] %= 10;```
### (4) 商和余数的求法商和余数处理:视被除数和除数的位数情况进行处理.
### 【例1】高精度加法。输入两个正整数,求它们的和。#### 【分析】 输入两个数到两个变量中,然后用赋值语句求它们的和,输出。但是,我们知道,在C++语言中任何数据类型都有一定的表示范围。而当两个被加数很大时,上述算法显然不能求出精确解,因此我们需要寻求另外一种方法。在读小学时,我们做加法都采用竖式方法,如图1。 这样,我们方便写出两个整数相加的算法。 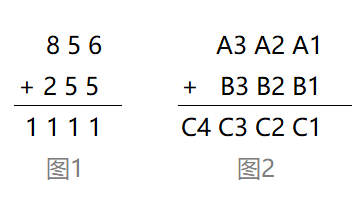 如果我们用数组A、B分别存储加数和被加数,用数组C存储结果。则上例有A[1]=6,A[2]=5, A[3]=8,B[1]=5,B[2]=5,B[3]=2,C[4]=1,C[3]=1,C[2]=1,C[1]=1,两数相加如图2所示。 ```cpp//因此,算法描述如下:int c[100];void add(int a[],int b[]) //a,b,c都为数组,分别存储被加数、加数、结果{ int i=1,x=0; //x是进位 while ((i<=a数组长度)||(i<=b数组的长度)) { c[i]=a[i]+b[i]+x; //第i位相加并加上次的进位 x=c[i]/10; //向高位进位 c[i]%=10; //存储第i位的值 i++; //位置下标变量 }}```### 参考代码
```cpp#include<bits/stdc++.h>using namespace std;const int N=1000000+5;long long a[N],b[N],c[N],base=10;char tmp[N];int main(){cin>>tmp;int n=strlen(tmp); for(int i=0;i<n;i++)a[i]=tmp[n-i-1]-‘0‘; cin>>tmp;int m=strlen(tmp);for(int i=0;i<m;i++)b[i]=tmp[m-i-1]-‘0‘;memset(c,0,sizeof(c));int up=max(n,m);for(int i=0;i<up;i++){c[i]+=a[i]+b[i]; c[i+1]+=c[i]/base;c[i]=c[i]%base;}if(c[up]) up++;for(int i=up-1;i>=0;i--) printf("%d",c[i]);puts("");return 0;}```
### 【例2】高精度减法。输入两个正整数,求它们的差。#### 【算法分析】类似加法,可以用竖式求减法。在做减法运算时,需要注意的是:被减数必须比减数大,同时需要处理借位。高精度减法的参考程序:
大数减小数做法:```cpp//大数减小数#include<bits/stdc++.h>using namespace std;const int N=100000+5;int a[N],b[N],c[N],base=10;char tmp[N];int main(){cin>>tmp;int n=strlen(tmp); for(int i=0;i<n;i++)a[i]=tmp[n-i-1]-‘0‘; cin>>tmp;int m=strlen(tmp);for(int i=0;i<m;i++)b[i]=tmp[m-i-1]-‘0‘;memset(c,0,sizeof(c));int up=max(n,m);for(int i=0;i<up;i++){c[i]=a[i]-b[i];if(c[i]<0) c[i+1]--,c[i]+=base;}while(!c[up-1]&&up>1) up--;for(int i=up-1;i>=0;i--) printf("%d",c[i]);puts("");return 0;}```大数减大数
```cpp//大数减大数#include<bits/stdc++.h>using namespace std;long long a[100010],b[100010],c[100010],lena,lenb,lenc,i;char n[100010],n1[100010],n2[100010];int main(){memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(c,0,sizeof(c));cin>>n1;cin>>n2;if(strlen(n1)<strlen(n2)||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0)){strcpy(n,n1);strcpy(n1,n2);strcpy(n2,n);cout<<"-";}lena=strlen(n1);lenb=strlen(n2);for(i=0;i<=lena-1;i++)a[lena-i]=int(n1[i]-‘0‘);for(i=0;i<=lenb-1;i++)b[lenb-i]=int(n2[i]-‘0‘);i=1;while(i<=lena||i<=lenb){if(a[i]<b[i]) a[i]+=10,a[i+1]--;c[i]=a[i]-b[i];i++;}lenc=i;while((c[lenc]==0)&&(lenc>1)) lenc--;for(i=lenc;i>=1;i--)cout<<c[i];cout<<endl;return 0; }```### 【例3】高精度乘法。输入两个正整数,求它们的积。#### 【算法分析】类似加法,可以用竖式求乘法。在做乘法运算时,同样也有进位,同时对每一位进行乘法运算时,必须进行错位相加,如图3、图4。
分析c数组下标的变化规律,可以写出如下关系式:ci = c’i +c”i +…由此可见,c i跟a[i]*b[j]乘积有关,跟上次的进位有关,还跟原c i的值有关,分析下标规律,有c[i+j-1]= a[i]*b[j]+ x + c[i+j-1]; x=c[i+j-1]/10 ; c[i+j-1]%=10;
### 参考代码高精乘低精```cpp#include<bits/stdc++.h>using namespace std;const int N=100000+5;int a[N],b,c[N],base=10;char tmp[N];int main(){gets(tmp);int n=strlen(tmp); for(int i=0;i<n;i++)a[i]=tmp[n-i-1]-‘0‘; int b;scanf("%d",&b);memset(c,0,sizeof(c));int up=n;for(int i=0;i<up;i++){c[i]+=a[i]*b;c[i+1]+=c[i]/base;c[i]=c[i]%base; }if(c[up]) up++;while(c[up]>base) c[up+1]+=c[up]%base,c[up]=c[up]%base,up++; for(int i=up-1;i>=0;i--) printf("%d",c[i]);puts("");return 0;}```高精乘高精
```cpp#include<bits/stdc++.h>using namespace std;const int N=100000+5;int a[N],b[N],c[N],base=10;char tmp[N];int main(){cin>>tmp;int n=strlen(tmp); for(int i=0;i<n;i++)a[i]=tmp[n-i-1]-‘0‘; cin>>tmp;int m=strlen(tmp); for(int i=0;i<m;i++)b[i]=tmp[m-i-1]-‘0‘; memset(c,0,sizeof(c));for(int i=0;i<n;i++)for(int j=0;j<m;j++)c[i+j]+=a[i]*b[j];int up=n+m-1;for(int i=0;i<up;i++){c[i+1]+=c[i]/base;c[i]=c[i]%base;}if(c[up]) up++;if(c[up-1]==0){cout<<0<<endl;return 0;}for(int i=up-1;i>=0;i--) printf("%d",c[i]);puts("");return 0;}
```
以上是关于模板高精算法的主要内容,如果未能解决你的问题,请参考以下文章