数据结构 -- 二叉树（Binary Search Tree）

Posted 2020-11-30 fondwang

一、简介

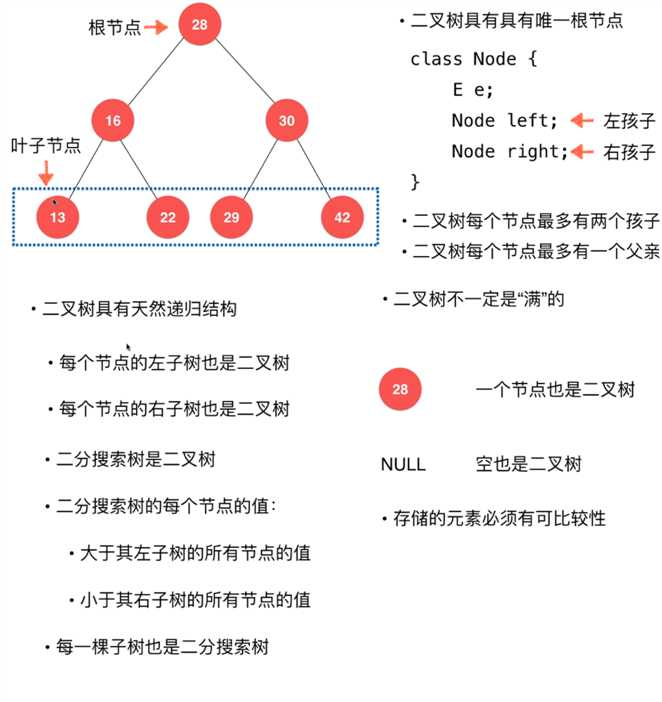
　　在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

　　一棵深度为k，且有2^k-1个结点的二叉树，称为满二叉树。这种树的特点是每一层上的结点数都是最大结点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且或者最后一层是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有（2的k-1次方）个叶子结点，至多有2^k-1个结点。

　　节点特性：1. 每个节点的值都大于其左子树的所有节点的值。

　　　　　　    2. 每个节点的值都小于其右子树的所有节点的值。

二、代码

 　　1.定义一个支持泛型的节点类, 用于存储二分搜索树每个节点的信息, 这个类作为二分搜索树的一个内部类, 二分搜索树的类声明以及Node节点类

public class BinaryTree<E extends Comparable<E>> {
    // 根节点
    private Node root ;
    // 树容量
    private int size ;
    public BSTree() {
        this.root = null ;
        this.size = 0 ;
    }
    public boolean isEmpty() {
        return size == 0 ;
    }
    public int getSize(){
        return size;
    }
    // 二分搜索树节点类
    private class Node {
        public E e ;
        // 左右子树
        public Node left , right ;
        public Node(E e) {
            this.e = e ;
            this.left = null ;
            this.right = null ;
        }
    }
}

　　2. 添加操作：二分搜索树本身的递归特性, 可以很方便的使用递归实现向二分搜索树中添加元素。

    //添加元素
    public void add(E e){
        root = add(root, e);
    }
    //插入元素，递归算法。 返回插入新节点后二叉树的根
    private Node add(Node node, E e){
        //如果当前根节点为空，则直接创建该节点为根节点
        if(node == null){
            size ++;
            return new Node(e);
        }
        if(e.compareTo(node.e) < 0){ //添加元素e 小于 节点元素e，则从左边添加
            node.left = add(node.left,e);
        }else if (e.compareTo(node.e) > 0){ //添加元素e 大于 节点元素e，则从右边添加
            node.right = add(node.right,e);
        }
        return node;
    }

 　　3. 查找操作：二分搜索树没有下标, 针对二分搜索树的查找, 定义一个contains方法, 是否包含某个元素, 返回布尔型变量, 这个操作是递归的过程。

 //查询是否包含e元素
    public boolean contains(E e){
        return contains(root, e);
    }
    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){
        if (node == null){
            return false;
        }
        if (node == e){
            return true;
        }else if (e.compareTo(node.e) > 0){ //如果大于根节点元素，则向右子树递归遍历
            return contains(node.right, e);
        }else{ //如果小于根节点元素，则向左子树递归遍历
            return contains(node.left, e);
        }
    }

　　4. 遍历操作

遍历分类：

深度优先遍历 : 1. 前序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之前, 遍历顺序 : 当前节点->左孩子->右孩子 2. 中序遍历 : 对当前节点的遍历在对左右孩子节点的遍历中间, 遍历顺序 : 左孩子->当前节点->右孩子 3. 后序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之后, 遍历顺序 : 左孩子->右孩子->当前节点 广度优先遍历 : 1. 层序遍历 : 按层从左到右进行遍历

 前序遍历：最常用/自然的遍历方式：

（一）、递归写法　　

//二叉树的前序遍历
    public void preOrder(){
        preOrder(root);
    }
    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if (node == null){
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

（二）、非递归写法：通过栈实现二叉树遍历　

// 二分搜索树的非递归前序遍历
public void preOrderNR(){
    Stack<Node> stack = new Stack<>();
    stack.push(root);
    while (stack !=null){
        Node node = stack.pop();
        System.out.println(node.e);

        if(node.right != null){
            stack.push(node.right);
        }
        if(node.left != null) {
            stack.push(node.left);
        }
    }
}

 中序遍历：

//二叉树的中序遍历
    public void inOrder(){
        inOrder(root);
    }
    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){
        if (node == null){
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

 

后序遍历：

//二叉树的后序遍历
    public void postOrder(){
        postOrder(root);
    }
    // 中序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){
        if (node == null){
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

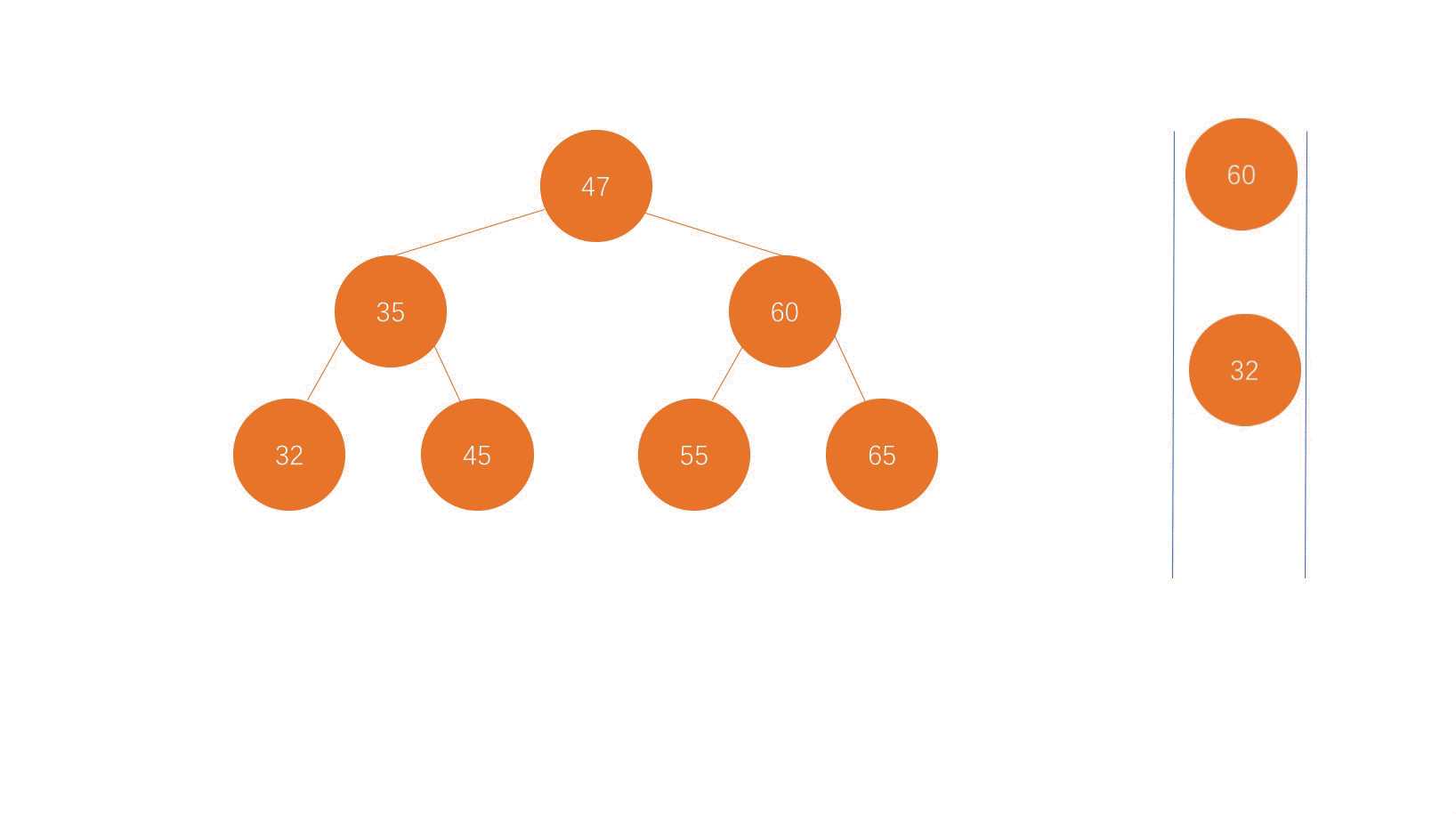
层序遍历： 

//二叉树的层序遍历
    public void levelOrder(){
        Queue<Node> queue = new LinkedList<>();
        queue.add(root); //先将最上层的根节点加入队列中
        while (!queue.isEmpty()){
            Node node = queue.remove(); //删除队列中的最低端的元素
            System.out.println(node.e); //打印输出

            //输出根节点后，将对应的左/右子树的元素添加到队列中。 队列是先进先出，所以先放左子树再放右子树
            if (node.left != null){
                queue.add(node.left);
            }
            if (node.right != null){
                queue.add(node.right);
            }
        }
    }

前,中,后序遍历总结
　　可以认为在遍历的时候每个节点要访问三次, 对当前节点进行遍历操作时一次, 访问当前节点左子树时一次, 访问当前节点右子树时一次, 可以认为前序遍历就是在第一次访问当前节点时进行操作, 以方便我们理解遍历结果, 下面几张图演示前中后序遍历的访问顺序, 蓝色的点表示在这次访问时对当前节点进行遍历操作

前序遍历示意图:　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　中序遍历示意图：　　　　　　　　　　　　　　　　　　　　　　　　　　　　后续遍历示意图：

 

 

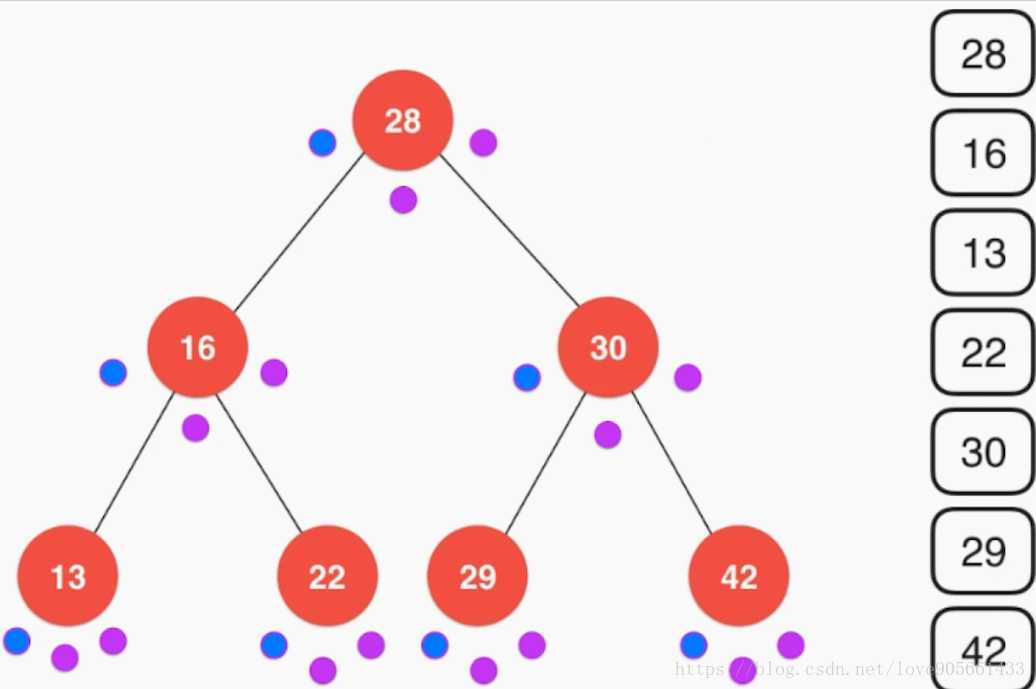
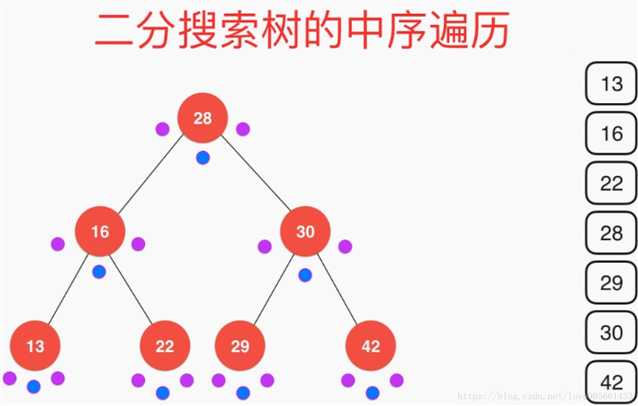
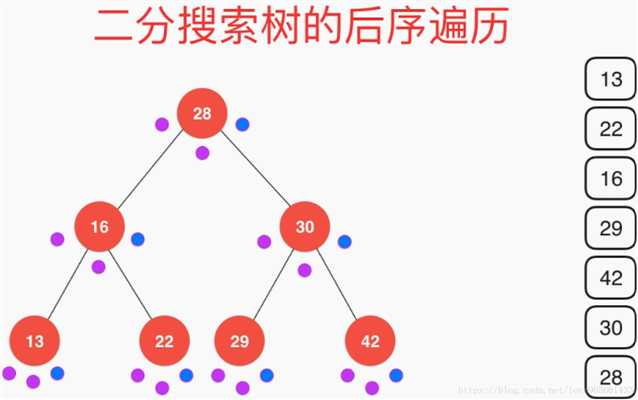
 层序遍历示例图：

 

 

 

 

原文链接：https://blog.csdn.net/love905661433/article/details/82981527