C++回溯法学习&练习
Posted 图灵奖未来得主
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++回溯法学习&练习相关的知识,希望对你有一定的参考价值。
C++回溯法学习&练习
写在前面
参考视频:
带你学透回溯算法(理论篇)| 回溯法精讲!
带你学透回溯算法-组合问题(对应力扣题目:77.组合)| 回溯法精讲!
【labuladong】回溯算法核心套路详解
基础理论
1.是递归函数的下半部分,递归与回溯相辅相成,回溯函数及递归函数。
2.回溯其实是纯暴力搜索。
3.可解问题:
组合问题: 1234进行组合包含两个数,12,13,14,23,24,34
切割问题:给一个字符串问在一些特定的条件下,如何切割。(例如条件问每一个字串为回文子串)
子集问题:求集合1,2,3,4的子集
排列问题:在组合问题上强调元素的顺序
棋盘问题:n皇后问题
4.回溯法一般都可以抽象为一颗n叉树
5.回溯法模板:
递归函数一般没有返回值
回溯算法的时间复杂度一般都非常高。
List<Value> result;
void backtrack(路径,选择列表)
if(终止条件)
result.add(路径);
return;
for(选择集合)
做选择;
backtrack(路径,选择列表);
撤销选择;
return;
与多叉树遍历的代码框架类似:
void traverse(TreeNode)
if (root == null)
return;
for (TreeNode child : root.children)
traverse(child);
回溯算法相当于:递归里面嵌套for循环
回溯三部曲:
1.确定递归函数的参数和返回值
2.确定递归终止条件
3.确定单层递归逻辑
组合问题
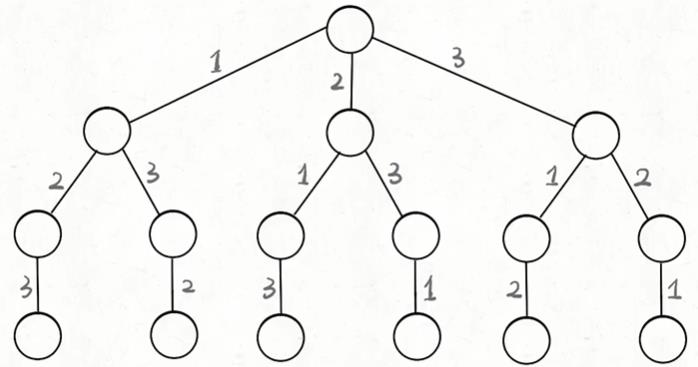
全排列:
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
input:
[1,2,3]
output:
[
[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]
]
构造多叉树:
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
vector<vector<int>> res;
//本题需要排除已经在track中的数字
bool ifcontains(vector<int> track, int x)
for (int i = 0; i < track.size(); i++)
if (track[i] == x)
return true;
return false;
void backtrack(vector<int> nums,vector<int> track)
//终止条件,到达叶子节点
//本题是路径长度和输入的整数序列长度相等
if(track.size()==nums.size())
res.push_back(track);
return;
//track用来存储走过的路径
//nums存储输入的整数序列
for (int i = 0; i < nums.size(); i++)
//排除不合法的选择
//本题中排除已经在track中的数字
if (ifcontains(track, nums[i]))
continue;
//做选择
track.push_back(nums[i]);
//递归
backtrack(nums, track);
//撤销选择
track.pop_back();
int main()
vector<int> nums, track;
int x;
while (cin>>x && getchar()!='\\n' )
nums.push_back(x);
nums.push_back(x);//输入待全排列的数列集合
backtrack(nums, track);
for (int i = 0; i < res.size(); i++)
for (int j = 0; j < nums.size(); j++)
cout << res[i][j] << " ";
cout << endl;
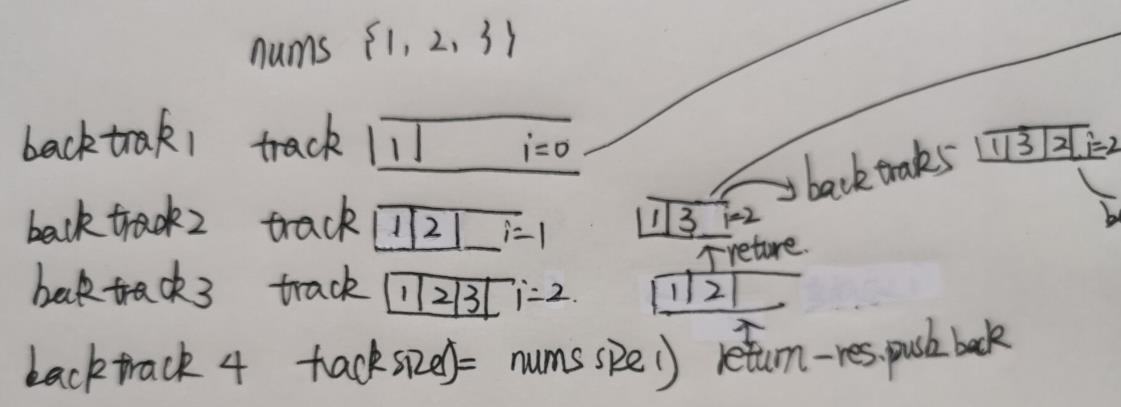
下面进行了手动递归可以帮助理解,局部变量i在回溯过程中是从原来的值继续进行的,比如backtrack4返回backtrack3后,i仍然保持原来在backtrack3时的值继续进行,由于+1后跳出循环直接返回上一层递归,即backtrack2。
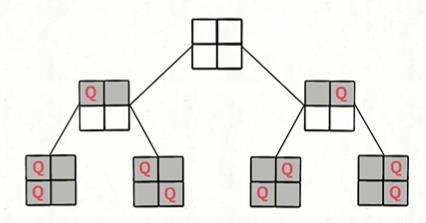
n皇后问题:
示例:
input:n=1
output:[[“Q”]]
一个简单的多叉树,很显然下面这种情况下没有可行解。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <string>
using namespace std;
vector<vector<string>> res;
//用来保存所有的可行解
//用于判断Q的放置是否符和八个方向的限定
//用于剪枝
//由于我们按照从上到下的顺序放置Q,所以下方一定不会有阻碍
//由于我们每行只放置一个Q,所以横向必须要考虑
//所以只需要考虑上方、左上、右上三个方向
bool isValid(vector<string> track, int x, int y)
for (int i = 0; i < x; i++)
if (track[i][y] == 'Q')
return false;
for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--,j--)
if (track[i][j] == 'Q')
return false;
for (int i = x - 1, j = y + 1; i >= 0 && j < track.size(); i--,j++)
if (track[i][j] == 'Q')
return false;
return true;
void backtrack(vector<string> track ,int row)
//终止条件
if (row==track.size())
res.push_back(track);
return;
for (int j = 0; j <track.size() ; j++)
if (!isValid(track, row, j))
continue;
//做选择
track[row][j] = 'Q';
//回溯
backtrack(track, row+1);
//撤销选择
track[row][j] = '.';
return;
int main()
int n, row = 0;
//用来记录已经标记的行数
cin >> n;
vector<string> track(n, string(n, '.'));
//这里的赋值方法需要记住
backtrack(track, row);
cout << "一共有" << res.size() << "种解" << endl<<endl;
for (int i = 0; i < res.size(); i++)
cout << "第" << i+1 << "种解为:" << endl;
for (int j = 0; j < res[i].size(); j++)
cout << res[i][j] << endl;
cout << endl;
作业部分
0-1背包问题
有n=20个物品,背包最大可装载M=878Kg。物品重量和价值分别如下:
W=92,4,43,83,84,68,92,82,6,44,32,18,56,83,25,96,70,48,14,58,
V=44,46,90,72,91,40,75,35,8,54,78,40,77,15,61,17,75,29,75,63,
求最优背包价值。
这题说白了也是找子集问题,与第三题不同的便是需要记录最值,是输出最值,同时终止条件为再装下别的超过载重量。
这些题目把解空间树画出来就是成功一半了哈哈哈。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <string>
using namespace std;
static int M = 878, maxvalue = 0;
vector< vector<int> > res;
bool contains(vector<int> track, int i)
for (int j = 0; j < track.size(); j++)
if (track[j] == i)
return true;
return false;
void backtrack(int W[],int V[],vector<int> track,int weight,int value,int index)
if(maxvalue<value)
maxvalue=value;
for(int i=index;i<21;i++)
if(contains(track,i)|| weight+W[i]>M)
continue;
track.push_back(i);
weight+=W[i];
value+=V[i];
backtrack(W,V,track,weight,value,i+1);
track.pop_back();
weight-=W[i];
value-=V[i];
return;
int main()
int W[21] = 0, 92,4,43,83,84,68,92,82,6,44,32,18,56,83,25,96,70,48,14,58 ;
int V[21]= 0,44,46,90,72,91,40,75,35,8,54,78,40,77,15,61,17,75,29,75,63 ;
vector<int>track;
int weight = 0, value = 0,index=1;
backtrack(W, V, track, weight, value,index);
cout << maxvalue;
子集问题
给定一个整数集合和一个整数,利用回溯法从集合中找出元素之和等于给定整数的所有子集。例如,有集合2, 3, 4, 7, 9, 10, 12, 15, 18,给定数为 20,那么满足条件的子集为2,18、2,3,15.
backtrack的终止条件为元素和等于20。构造的树为:
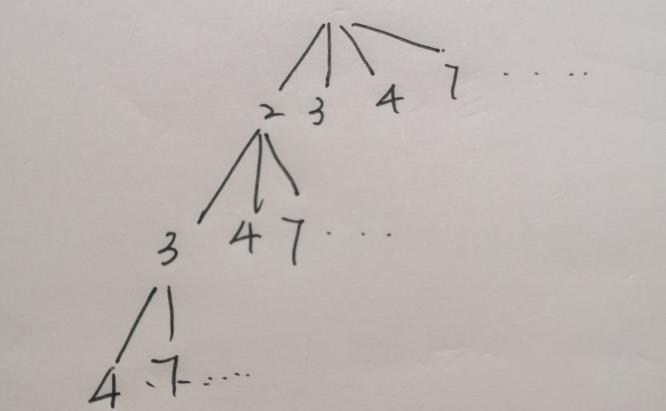
解的集合存入res,在集合范围内查找,下面的for循环便是从2循环到18,除去已选的元素、和大于20并且在track末端后面的元素的后,便push_back,进入子节点,进行递归,之后再进行回溯,撤销选择。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <string>
using namespace std;
vector<vector<int>> res;
int sum(vector<int>track)
int sum=0;
for (int i = 0; i < track.size(); i++)
sum += track[i];
return sum;
int contains(vector<int>track, int x)
for (int i = 0; i < track.size(); i++)
if (track[i] == x)
return true;
return false;
void backtrack(vector<int>track, vector<int>arr, int index)
//终止条件
if (sum(track) == 20)
res.push_back(track);
return;
//依次遍历每个元素作为track的第一个元素
for (int i = index; i < arr.size(); i++)
//排除不可以进入track的元素
if (contains(track, arr[i]) || sum(track) + arr[i] > 20)
continue;
//做选择
track.push_back(arr[i]);
//递归
backtrack(track, arr, i+1);
//这里注意不能重复查找需要index=i+1
//在下一层循环才不会重复
//撤销选择
track.pop_back();
return;
int main()
int x,index=0;
vector<int> arr, track;
while (cin >> x && getchar() != '\\n')
arr.push_back(x);
arr.push_back(x);
backtrack(track, arr, index);
cout << "共有" << res.size() << "个满足条件的子集" << endl;
for (int i = 0; i < res.size(); i++)
cout << "" << res[i][0];
for (int j = 1; j < res[i].size(); j++)
cout << ", " << res[i][j];
cout <<''<< endl;
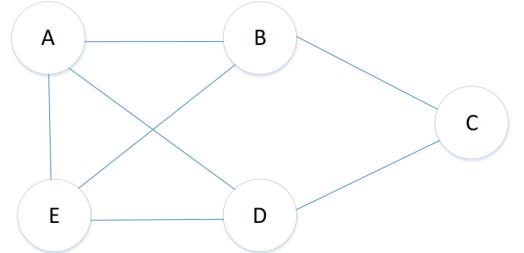
三着色问题
利用回溯法求解三着色问题。即如何只用 3 种颜色对下图中的节点进行着色,使得有边相连的两个节点的颜色不同。给出你的着色方案。
写这题的时候属实给我整的有些懵,最终只能调出来输出一种解答的程序,知道有无大神给我改改程序。
只输出一种答案的程序思路为:依次考虑每一个节点,从A开始,backtrack终止条件为五个点全部着色,在for循环中,首先跳过已经着色的点后判断下一个点需不需要新颜色,这里依次判断已经选择过的颜色,所以backtrack函数还需要传入color,用于记录每层当前的color数,才好判断需不需要增添颜色。若是三个颜色不能够完成赋值便会直接从for后return。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <string>
using namespace std;
//存入图,用于剪枝
int G[5][5] = 0,1,0,1,1,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,