计蒜客习题：画图游戏（Havel-Hakimi定理）

Posted 2020-11-29 vikyanite

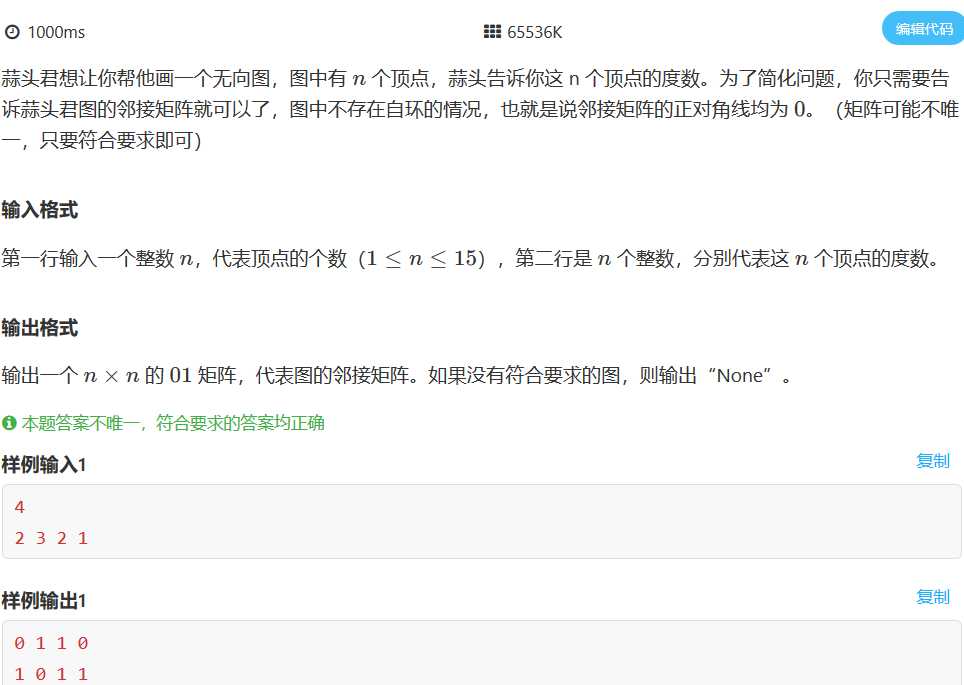
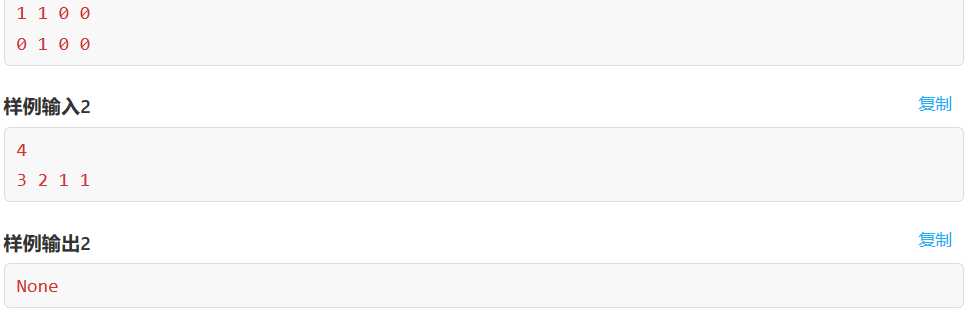
这道题在如何判断能否存图上想了好久，最后还是参考了网上的题解就了解到了这样一个定理——Havel-Hakimi定理

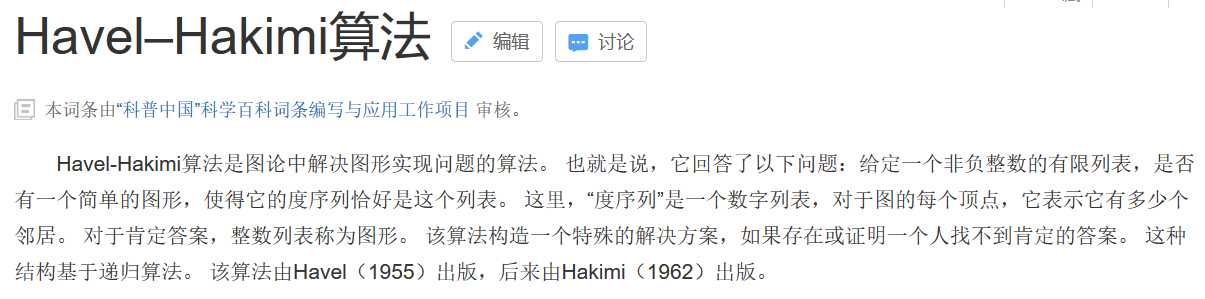
下面给出例子（例子转自https://blog.51cto.com/sbp810050504/883904）

比如序列：4 7 7 3 3 3 2 1

下标	1	2	3	4	5	6	7	8
值	4	7	7	3	3	3	2	1

 

第一步：把序列按降序排序。

下标	1	2	3	4	5	6	7	8
值	7	7	4	3	3	3	2	1

 

第二步：删除第一个数7。序列变成

下标	1	2	3	4	5	6	7
值	7	4	3	3	3	2	1

 

第三步：从头开始，数7个数，也就是下标：[1,7]把[1,7]区间里的值都减1

由于第一个数已经删除，那么序列变成这样的了：

下标	1	2	3	4	5	6	7
值	6	3	2	2	2	1	0

然后：

重复第一步：排序。

重复第二步：删除第一个数6

重复第三步：从头开始数6个数：也就是下标【1,6】，把区间【1，6】中的数删除。序列变成：

下标	1	2	3	4	5	6
值	2	1	1	1	0	-1

由于已经出现了-1，而一个点的边数（度）不可能为负数。所以，我们就可以判定序列无法构成一个图，所以此序列是不可图的。

下面再举一个例子：

已经排序：

5

4

3

3

2

2

2

1

1

1.

删除第一个数5：

4

3

3

2

2

2

1

1

1.

 

把前面5个数减1：

3

2

2

1

1

2

1

1

1.

排序：

3

2

2

2

1

1

1

1

1.

删除第一个数3：

 

2

2

2

1

1

1

1

1.

把前面3个数减1：

1

1

1

1

1

1

1

1.

排序：

1

1

1

1

1

1

1

1.

删除第一个数1：

1

1

1

1

1

1

1.

把前面1个数减1：

0

1

1

1

1

1

1.

排序：

1

1

1

1

1

1

0

删除第一个数1：

1

1

1

1

1

0

把前面1个数减1：

0

1

1

1

1

0

排序：

1

1

1

1

0

0

              

依此类推：到最后只剩下：

0

0

0

0

由此判断该序列是可图的。

 

附上AC代码：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define maxn 1000 + 5
struct node{
    int pos;
    int degree;
}a[maxn];
int ans[maxn][maxn];
bool cmp (node a,node b){
    return a.degree > b.degree;
}
int main()
{
    int n, x = 0;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i].degree;
        a[i].pos = i;
        if (!a[i].degree) x++;
    }
    //由Havel–Hakimi可知不能成图的条件为：
    //当所有点的度不为都0且存在点的度为0
    //这样的话降序减下去，就必然出现度为负的点
    if (x != 0 && x != n) 
    {
        cout << "None
";
        return 0;
    }
    for (int i = 0; i < n; i++)
    {
        sort(a+i, a+n, cmp);
        if (a[i].degree==0) break;
        if(a[i].degree > n-1-i)
        {
            cout << "None";
            return 0;
        }
        for (int j = 1 + i; j <= a[i].degree + i; j++)
        {
            a[j].degree--;
            if (a[j].degree < 0)
            {
                cout << "None";
                return 0;
            }
            ans[a[i].pos][a[j].pos] = ans[a[j].pos][a[i].pos] = 1;
        }
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (j == 0) cout << ans[i][j];
            else cout << " " << ans[i][j];
        }
        cout << endl;
    }
    return 0;
}

View Code