Project Euler 54: Poker hands

Posted 2020-11-29 metaquant

在纸牌游戏中，一手包含五张牌并且每一手都有自己的排序，从低到高的顺序如下：

• 大牌：牌面数字最大
• 一对：两张牌有同样的数字
• 两对：两个不同的一对
• 三条：三张牌有同样的数字
• 顺子：所有五张牌的数字是连续的
• 同花：所有五张牌有同样的花色
• 船牌：三张同样数字的牌加一个一对
• 四条：四张牌有同样的数字
• 同花顺：牌面数字连续且有同样的花色
• 皇家同花顺：由(10,J,Q,K,A)五张牌构成的同花顺

十三张牌根据牌面数字从小到大排序为：(2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A)

如果两个玩家所持的一手牌排序相同，那么牌面数字较大的获胜。比如，一对八要大于一对五(见下面例一)。但是如果两手牌排序打平，比如两个玩家都有一对(Q)，那么比较剩下的牌中的最大者(见下面例四)。如果这张牌仍然打平，则比较其它剩下的牌中的最大者，依次类推。

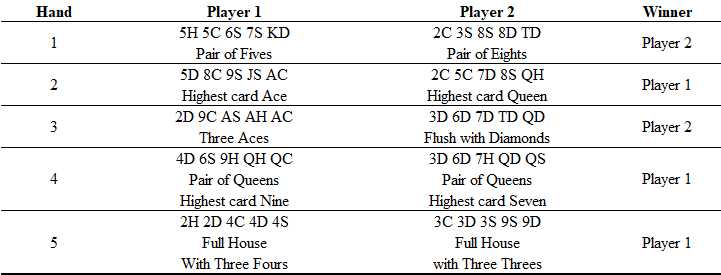
考虑两个玩家所持的下面五手牌，观察他们的胜负情况：

文本文件poker.txt中包含一千条随机生成的两个玩家的牌面数据，每一行包含十张牌(用一个空格分开)，前五张牌是第一个玩家的，后五张牌是第二个玩家的。你可以认为所有牌都是有效的，每个玩家所持的牌没有特定的顺序，并且在每一手牌中总有一个确定的获胜者。求在这一千手牌中玩家一获胜了多少次？

分析：这是我们到目前为止看到的文字最多的题目，而且我为了解决这个题目所写的代码也是到目前行数最多的。和以前的题目不同，这道题目的难点并不在于其中的数学原理，而是要对这个游戏的规则本身有清楚的了解，并且能够把这些规划用代码表示出来。题目本身介绍规则的介绍不是很清楚，我建议大家参考这篇维基百科，里面对这个游戏的规则有更透彻清晰的介绍。总结起来游戏的规则有这么几条：第一，每一手牌有九个可能的排序(皇家同花顺就是同花顺，所以不用单独考虑)，排序高的牌大于排序低的牌；第二，如果两手牌的排序相同，则需要根据这一手牌的不同类型来进行排序，总结起来也有两种情况：(1)如果类型中不涉及对子以及各种条牌，也就是同花顺、同花、顺子以及大牌这四种类型时，只需要对牌面数字形成的列表从大到小排序，然后比较两个列表即可。因为比较列表时，它会从第一个数字陆续向后比较，因此和这四种类型的牌的比较方式相同；(2)剩下五种涉及到对子和条牌的类型，也即四条、三条、船牌、二对和一对，则需要首先按条或者对分组，然后对条或者对中的牌面数字分别比较大小，这里可以用到python中Counter这个数据结构。

由于解题过程涉及大量的逻辑判断，为了让代码结构更加清晰，我使用了面向对象的方式来组织代码。我编写了两个类：第一类是纸牌类，它有两个属性，分别是花色与牌面数字，为了让之后的比较更加方便，我把(T,J,Q,K,A)五个牌面分别映射至对应的数字。第二个类表示五张牌形成的一手，这个类有八个属性，分别表示五张牌的牌面数字、五张牌的花色、五张牌牌面数字的分组统计、第一个分组的牌面数字、第二个分组的牌面数字、五张牌花色的类型数量、五张牌面数字从大到小排序的列表以及五张牌从大到小排序后，前后两个数字之差构成的集合。此外，这个类有两个方法：第一个方法用来判断这一手牌的类型，返回每一手牌的类型名称以及类型排序；第二个方法用来比较这一手牌和另一手牌的大小，使用的是我们前面总结的比较各手之间大小的规则。

最后，我们从文本文件中导入数据，把每一行数据拆分为第一个玩家和第二个玩家，并记录第一个玩家获胜的次数，最后返回这个次数即为题目所求。代码如下：

# time cost = 42.1 ms ± 157 μs

from collections import Counter

class Card:
    def __init__(self,vs):
        d = {'T':10,'J':11,'Q':12,'K':13,'A':14}
        self.s = vs[1]        
        if vs[0] not in set('TJQKA'):
            self.v = int(vs[0])
        else:
            self.v = d[vs[0]]
        
class Hand:
    def __init__(self,cards):
        self.values = [x.v for x in cards]
        self.suits = [x.s for x in cards]
        self.value_counter = Counter(self.values).most_common()
        self.fc = self.value_counter[0][1]
        self.sc = self.value_counter[1][1]
        self.suit_kind = len(set(self.suits))
        self.ranks = sorted([x.v for x in cards],reverse=True)
        self.diff = set([self.ranks[:-1][i]-self.ranks[1:][i] for i in range(4)])
    
    def categories(self):
        if self.suit_kind == 1 and self.diff == {1}:
            return ('Straight Flush',9)
        elif self.suit_kind == 1:
            return ('Flush',6)
        elif self.diff == {1}:
            return ('Straight',5)
        elif self.fc == 4:
            return ('Four of a Kind',8)
        elif self.fc == 3 and self.sc == 2:
            return ('Full House',7)
        elif self.fc == 3 and self.sc == 1:
            return ('Three of a Kind',4)
        elif self.fc == 2 and self.sc == 2:
            return ('Two Pairs',3)
        elif len(self.value_counter) == 4 and self.fc == 2:
            return ('One Pair',2)
        else:
            return ('High Card',1)
    
    def is_winner(self,hand):
        if self.categories()[1] > hand.categories()[1]:
            return True
        elif self.categories()[1] < hand.categories()[1]:
            return False
        elif self.categories()[1] in [8,7,4,3,2]:
            return self.value_counter > hand.value_counter
        else:
            return self.ranks > hand.ranks

def main():
    count = 0
    with open('data/ep54.txt') as f:
        hands = [line.split() for line in f]
    for hand in hands:
        p1_cards = [Card(x) for x in hand[:5]]
        p2_cards = [Card(x) for x in hand[5:]]
        p1_hand,p2_hand = Hand(p1_cards),Hand(p2_cards)
        if p1_hand.is_winner(p2_hand):
            count += 1
    return count