图论复习H

Posted 2020-11-29 lin4xu

题意：求桥与同时位于两个环中的边的个数

分析：虽然这不是分享题，没必要写的非常详细，但这的确又刷新了我对tarjan的认识与理解

求桥不用多说，再不会可以找豆腐撞s了

这里主要是这个同时位于两个环中的边的个数“冲突边”

先说结论，当且仅当一个环中，边数多于点数，那么这个环中所有的边都是“冲突边”

首先，反正我在搞懂之前，每次都要犹豫很久，这个环到底是点双？边双？还是强连通分量？（只会用tarjan求这仨）

其实，这个环一定是由点组成的环，直接排除边双，而这个是无向图，一般不讨论强连通分量的事，因为显然都能互相到达

所以，这里的环实际上指的是点双

再稍微验证一下这个结论（具体证明的话其实你看我验证一下就很明确了，非要证明的话我没往深里想，反正这也不是分享题）

 

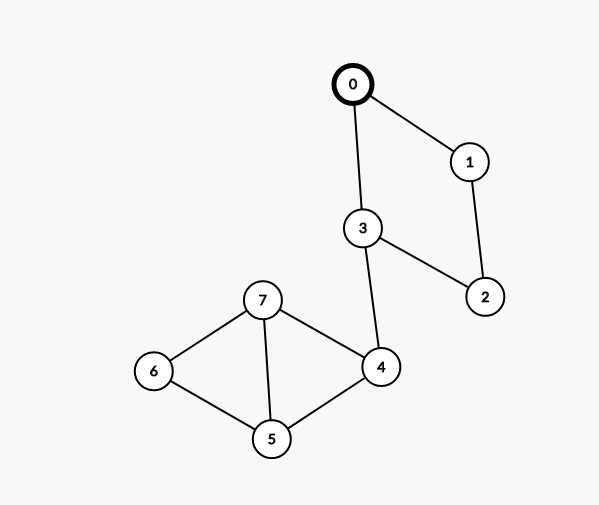
 首先，下面的4567一共出现了三个环，分别是4567,457,567

显然每条边都是冲突的（根据定义，两个环共用的边是冲突的），比如67这条边被4567与567共用，57被567与457共用等

而0123显然是没事的

那么问题来了，点双中点的个数很好求，边的个数怎么求

点可以开个vector，和平常一样的求法

边呢？

也可以开个vector

点的vector代表访问点的顺序

边呢？

也表示边的访问顺序

先放一下代码

void tarjan(int x,int id)
{
    dfn[x]=low[x]=++tar_cnt;
    for(int i=head[x];~i;i=e[i].next)
    {
        if(i==(id^1)) continue;
        int v=e[i].to;
        if(!dfn[v])
        {
            q.push_back(i);
            tarjan(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfn[x]) e_cnt++;
            if(low[v]>=dfn[x])
            {
                int nowans=0,now;
                s.clear();
                do
                {
                    nowans++;
                    now=q.back();
                    q.pop_back();
                    s.insert(e[now].from);
                    s.insert(e[now].to);
                }while(now!=i);
                if(nowans>s.size()) ans+=nowans;
            }
        }
        else if(dfn[v]<dfn[x]) q.push_back(i),low[x]=min(low[x],dfn[v]);
    }
}

先看看最原始的求点双与桥的代码框架

void tarjan(int x,int id)
{
    dfn[x]=low[x]=++tar_cnt;
    for(int i=head[x];~i;i=e[i].next)
    {
        if(i==(id^1)) continue;
        int v=e[i].to;
        if(!dfn[v])
        {
            tarjan(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfn[x]) e_cnt++;
            if(low[v]>=dfn[x])
            {
        
            }
        }
        else low[x]=min(low[x],dfn[v]);
    }
}

那么，我们先把不一样的地方标记一下，然后每个地方慢慢解释

void tarjan(int x,int id)
{
    dfn[x]=low[x]=++tar_cnt;
    for(int i=head[x];~i;i=e[i].next)
    {
        if(i==(id^1)) continue;
        int v=e[i].to;
        if(!dfn[v])
        {
            q.push_back(i);
            tarjan(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfn[x]) e_cnt++;
            if(low[v]>=dfn[x])
            {
                int nowans=0,now;
                s.clear();
                do
                {
                    nowans++;
                    now=q.back();
                    q.pop_back();
                    s.insert(e[now].from);
                    s.insert(e[now].to);
                }while(now!=i);
                if(nowans>s.size()) ans+=nowans;
            }
        }
        else if(dfn[v]<dfn[x]) q.push_back(i),low[x]=min(low[x],dfn[v]);
    }
}

大体分成这三块

首先是红色，这里就是个加边的操作，

但值得注意的是，这里其实是将所有的边都加入了栈中

而不是只加入dfs顺序中的边

当然这里你肯定有疑问为什么这样能加入所有的边（不多且不少）

那就接着往下看黄色的

先说结论，这句话的作用是防止同一条边，他的反向边也被加入栈中

显然，如果没有这句话，除了儿子直接访问父亲的反向边外，所有的边都会加入栈中

但加入这句话后，每条dfs顺序以外的边都会以返祖边的形式加入，而不是以祖先连向孩子的形式加入，比如

 

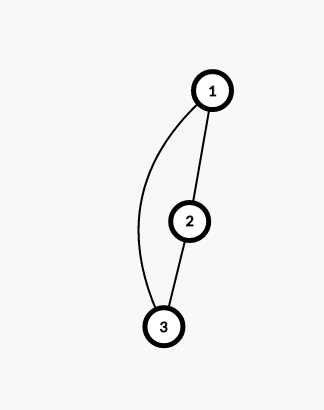
 这样一棵简单的tarjan产生的“树”，如果不加这句话的话，1->2,2->3,3->1,1->3都会加入栈中，而加这句话后，只有1->2,2->3,3->1会加入栈中

红色和黄色加在一起保证了所有的边均会加入栈中有且仅有一次

接下来就是绿色部分

咱们先把上面的图修饰一下，然后模拟一下过程

 

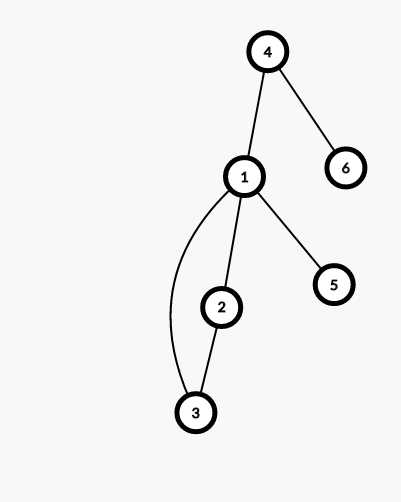
 前面的过程先省略一下，直接到节点1开始tarjan时开始（假设1先访问的2，按照图上的方式建树）

目前栈中当做啥也没有

1访问到2

边12入栈

2访问到3

边23入栈

3访问到1

边31入栈

注意这时不能继续从1往下dfs，这只是一条返祖边

然后点开始退栈（这里明面上并没有给点弄个栈，不过dfs不就是类似的退栈过程，这里就是个表达的方式）

点3退栈

点2退栈

这时，点1知道了自己是割点，并且找出了123这个点双以及其所有的边12,23,31

是不是感觉很神奇？

再来一个例子

 

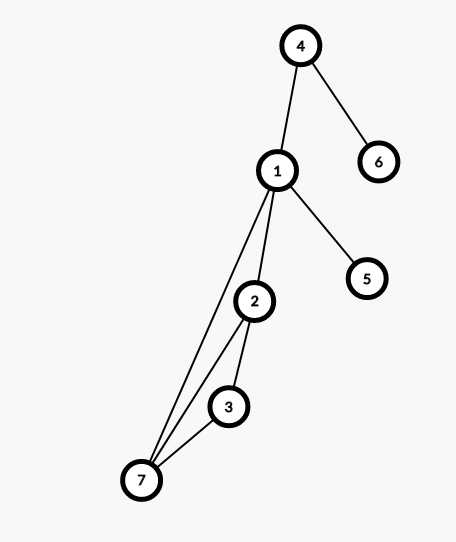
 还是1访问到2

12进栈

2访问到3

23进栈

3访问到7

37进栈

下面其实有很多种走法，我就选择我认为大家最想看的走法去走

7找到1

71进栈

7又找到2

72进栈

然后7,3,2依次弹栈

发现回到1时，点双里的点与边又都找到了

其实，这两个过程表达的是，在回到割点的时候，他的子树一定都被处理完了，自然边和点都会完整的加入栈中

往上翻有点麻烦，我再给你复制一下这段代码

if(low[v]>=dfn[x])
            {
                int nowans=0,now;
                s.clear();
                do
                {
                    nowans++;
                    now=q.back();
                    q.pop_back();
                    s.insert(e[now].from);
                    s.insert(e[now].to);
                }while(now!=i);
                if(nowans>s.size()) ans+=nowans;
            }

这里的ans是统计总的“冲突边”数量，nowans是当前点双中边的数量，这里的s是set，用来去重并找到点双的元素个数

这里求元素个数也可以和以前一样再开一个vector存点的入栈顺序，都是可以的，你可以任选一种做法

当然最后要在来的那条边处停止

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<set>
using namespace std;

const int maxn=1e4+1;
const int maxm=1e5+1;

struct Node
{
    int from,to,next;
}e[maxm<<1];
int dfn[maxn];
int low[maxn];
int head[maxn];
vector<int> q;
set<int> s;
int cnt,tar_cnt,e_cnt,b_cnt,ans;

void add(int x,int y)
{
    e[cnt].to=y;
    e[cnt].from=x;
    e[cnt].next=head[x];
    head[x]=cnt++;
}

void tarjan(int x,int id)
{
    dfn[x]=low[x]=++tar_cnt;
    for(int i=head[x];~i;i=e[i].next)
    {
        if(i==(id^1)) continue;
        int v=e[i].to;
        if(!dfn[v])
        {
            q.push_back(i);
            tarjan(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfn[x]) e_cnt++;
            if(low[v]>=dfn[x])
            {
                int nowans=0,now;
                s.clear();
                do
                {
                    nowans++;
                    now=q.back();
                    q.pop_back();
                    s.insert(e[now].from);
                    s.insert(e[now].to);
                }while(now!=i);
                if(nowans>s.size()) ans+=nowans;
            }
        }
        else if(dfn[v]<dfn[x]) q.push_back(i),low[x]=min(low[x],dfn[v]);
    }
}

int main()
{
    int n,m,x,y;
    while(scanf("%d%d",&n,&m)!=EOF&&n)
    {
        memset(dfn,0,sizeof(dfn));
        memset(low,0,sizeof(low));
        memset(head,-1,sizeof(head));
        q.clear();cnt=tar_cnt=e_cnt=b_cnt=ans=0;
        while(m--)
        {
            scanf("%d%d",&x,&y);
            add(x,y);add(y,x);
        }
        for(int i=0;i<n;i++) if(!dfn[i]) tarjan(i,-1);
        printf("%d %d
",e_cnt,ans);
    }
    return 0;
}