Anton and School - 2 （范德蒙恒等式模板）

Posted 2020-11-29 shallow-dream

As you probably know, Anton goes to school. One of the school subjects that Anton studies is Bracketology. On the Bracketology lessons students usually learn different sequences that consist of round brackets (characters "(" and ")" (without quotes)).

On the last lesson Anton learned about the regular simple bracket sequences (RSBS). A bracket sequence s of length n is an RSBS if the following conditions are met:

• It is not empty (that is n ≠ 0).
• The length of the sequence is even.
• First  charactes of the sequence are equal to "(".
• Last  charactes of the sequence are equal to ")".

For example, the sequence "((()))" is an RSBS but the sequences "((())" and "(()())" are not RSBS.

Elena Ivanovna, Anton‘s teacher, gave him the following task as a homework. Given a bracket sequence s. Find the number of its distinct subsequences such that they are RSBS. Note that a subsequence of s is a string that can be obtained from s by deleting some of its elements. Two subsequences are considered distinct if distinct sets of positions are deleted.

Because the answer can be very big and Anton‘s teacher doesn‘t like big numbers, she asks Anton to find the answer modulo 10⁹ + 7.

Anton thought of this task for a very long time, but he still doesn‘t know how to solve it. Help Anton to solve this task and write a program that finds the answer for it!

Input

The only line of the input contains a string s — the bracket sequence given in Anton‘s homework. The string consists only of characters "(" and ")" (without quotes). It‘s guaranteed that the string is not empty and its length doesn‘t exceed 200 000.

Output

Output one number — the answer for the task modulo 10⁹ + 7.

Examples

Input

)(()()

Output

6

Input

()()()

Output

7

Input

)))

Output

0

Note

In the first sample the following subsequences are possible:

• If we delete characters at the positions 1 and 5 (numbering starts with one), we will get the subsequence "(())".
• If we delete characters at the positions 1, 2, 3 and 4, we will get the subsequence "()".
• If we delete characters at the positions 1, 2, 4 and 5, we will get the subsequence "()".
• If we delete characters at the positions 1, 2, 5 and 6, we will get the subsequence "()".
• If we delete characters at the positions 1, 3, 4 and 5, we will get the subsequence "()".
• If we delete characters at the positions 1, 3, 5 and 6, we will get the subsequence "()".

The rest of the subsequnces are not RSBS. So we got 6 distinct subsequences that are RSBS, so the answer is 6.

题解：范德蒙恒等式（快速幂+逆元+排列组合)

 

 

 

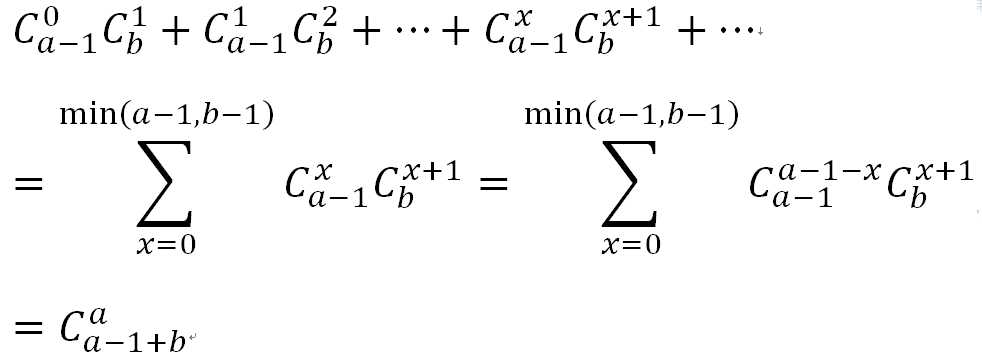
这个题就是用上面来写，图中的a 就是 L【i】，b就是R【i】，也就是如果从左边再选出X个，右边就要选出X+1个来对应。0<= X <=min（L【i】-1 ， R【i】）；然后把所有的情况加起来取模，就是答案

 写的时候，cin输入，从0开始计算l,r数组，结果出错了，strlen(str)一定要记录下来，不然T到自闭（我太菜了，没想到这个原因）

 

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 #include <string>
 5 #include <vector>
 6 #include <map>
 7 #include <set>
 8 #include <list>
 9 #include <deque>
10 #include <queue>
11 #include <stack>
12 #include <cstdlib>
13 #include <cstdio>
14 #include <cmath>
15 #include <iomanip>
16 #define ull unsigned long long
17 #define ll long long
18 #define pb push_back
19 #define rep(i,start,end) for(int i=start;i<=end;i++)
20 #define per(i,end,start) for(int i=end;i>=start;i--)
21 #define tle ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
22 #define lc now<<1
23 #define rc now<<1|1
24 using namespace std;
25 const int mod = 1000000007 ; ///998244353;
26 const int mxn = 2e5 +7;
27 ll _,n,m,t,k,u,v,ans,cnt,ok,lim;
28 int  l[mxn] ,  r[mxn] ;
29 ll dp[mxn] , inv[mxn];
30 char str[mxn];
31 ll ksm(ll x, ll k)
32 {
33     ll ans = 1;
34     while(k)
35     {
36         if(k&1) ans=ans*x%mod;
37         x = x*x%mod;
38         k>>=1;
39     }
40     return ans;
41 }
42 ll C(ll n,ll m){return dp[n]%mod*inv[n-m]%mod*inv[m]%mod;}
43 int main()
44 {
45     tle;
46     dp[0]=1;inv[0] = 1 ;
47     rep(i,1,mxn) dp[i] = dp[i-1]*i%mod , inv[i] = ksm(dp[i] , mod-2);
48     scanf("%s",str+1);
49     int len = strlen(str+1) ;
50     rep(i,1,len) l[i] = ( str[i]==‘(‘?l[i-1]+1:l[i-1] );
51     per(i,len,1) r[i] = ( str[i]==‘)‘?r[i+1]+1:r[i+1] );
52     ll ans = 0 ;
53     for(int i=1;i<=len;i++)
54     {
55         if(str[i]==‘(‘)
56             ans = ( ans + C(l[i]+r[i]-1,l[i]) )%mod ;
57     }
58     printf("%lld
",(ans%mod));
59 }

 

以上是关于Anton and School - 2 （范德蒙恒等式模板）的主要内容，如果未能解决你的问题，请参考以下文章

D. Anton and School - 2 范德蒙恒等式

CodeForces 785 D Anton and School - 2 范德蒙恒等式

CF #404 (Div. 2) D. Anton and School - 2 (数论+范德蒙恒等式)

CodeForces 785D Anton and School - 2

CF785D Anton and School - 2（范德蒙德行列式卷积）

#404 （div2）Anton and School - 2