《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading

Posted 董小虫

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading相关的知识，希望对你有一定的参考价值。

一、光的物理特性

光与物体的交互形成了基于物理着色的基础。

在物理层面上，光的模型为电磁横波。每个波都有一个单一的波长 λ \\lambda λ。具有单一波长的光叫单色光（monochromatic light），如下图所示；实际上大部分光是多色光（polychromatic），具有很多不同的波长。


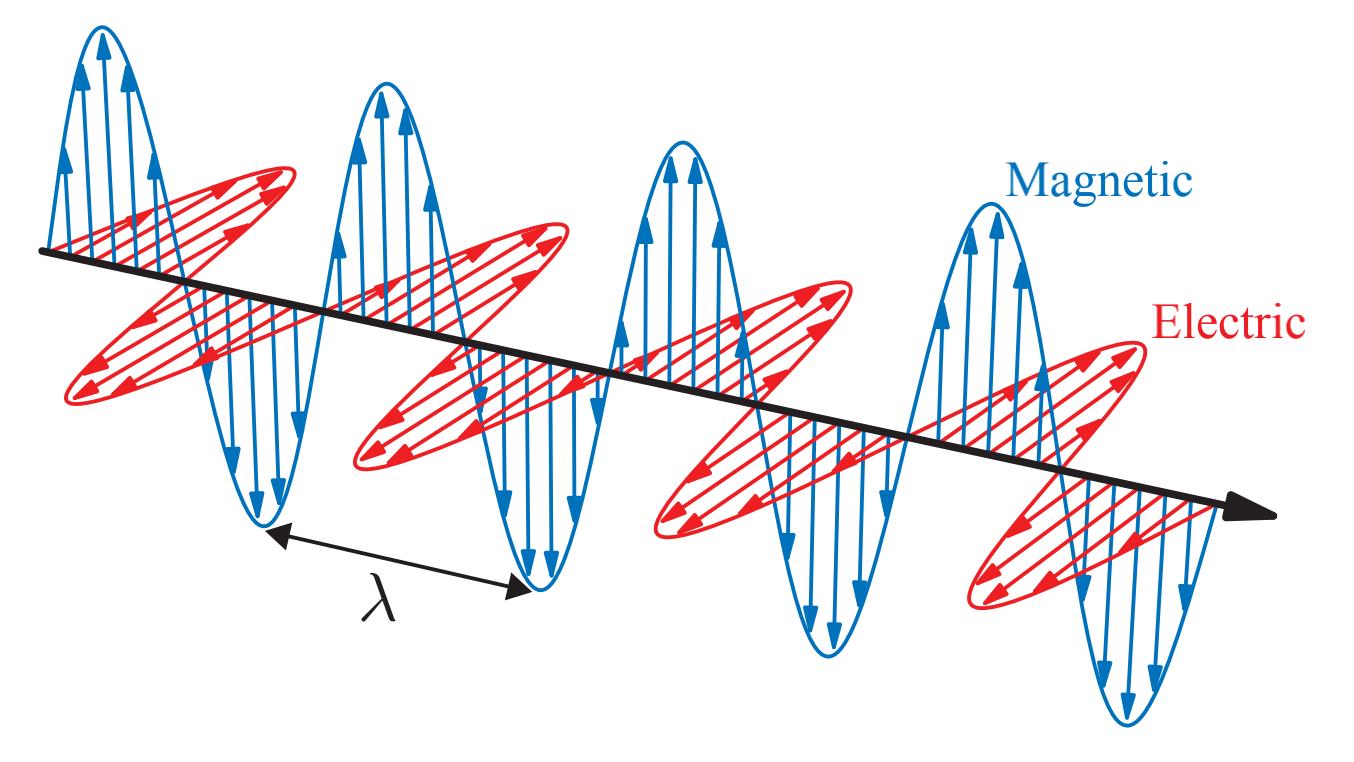
上图的光波是线性偏振（linear polarized），即电场和磁场分别沿着一条线前后移动；更常见的则是非偏振的（unpolarized）光。

真空光速恒定为 c c c，300000公里每秒。

可见光波长近似为400到700纳米。

光能量流密度为电场和磁场的乘积。通常情况下只考虑电场，因其产生影响更大。在渲染领域，关注时间范围内的平均能量流，这个值与振幅的平方成正比；这个平均能量密度为辐照度（irradiance），记为 E E E。

光的融合是线性的，即总的光波是各个分量的和。

  • 正向干涉（constructive interference）： E n = k ( n a ) 2 = n 2 E 1 E_n=k(na)^2=n^2E_1 En​=k(na)2=n2E1​
  • 负向干涉（destructive interference）： E n = k 0 2 = 0 E_n=k0^2=0 En​=k02=0
  • 相干叠加（coherent addition）：波峰和波谷以一种不变的形式相连。相干叠加的辐照度结果在 0 − n 2 0-n^2 0−n2倍单一波辐照度。

大部分情况下，波之间是不相干的（incoherent），即相位是相对随机的。这种情况下，合并后的振幅为 n a \\sqrtna n ​a，则单独波的辐照度可以按照线性得到 n n n倍的结果。

在渲染中，因电荷震动而发射部分能量的物体，当作光源处理。

散射（scattering）：震动的电磁场牵动物体的电荷震动，而震动的电荷又向其他方向发射能量，这种现象就叫散射。散射出的光波与原本的光波有相同的频率。不同频率的光与物体的交互互不干涉。

单个分子会朝所有方向散射，但是不同方向上强度不同：越靠近原方向的轴，散射的光越多；反之越少。高频的光更容易散射。

1.1 粒子

理想气体：分子之间无相互影响，位置完全随机，且不相关。这种情况下，从不同分子散射而来的光波相位是完全随机，且持续变化的；即可线性叠加。

当分子聚集时，聚团直径远远小于光波波长时，散射光的强度越大。这种现象直到聚团直径大于光波波长时，将不再上升。这种现象是云雾对光散射的基础。瑞利散射和丁达尔效应。

当粒子直径与光波波长相仿，散射现象称为米氏散射。

1.2 媒介

在均匀介质（homogeneous mediam）中，除了原光线传播方向，其他方向都会负向干涉。最终结果就是除了速度和振幅外，其他均与原光波相同，不存在任何散射。

折射率（index of refraction，IOR）：原光波的相位速度与新光波的相位速度之比，记为 n n n。

衰减率（attenuation index）：光穿过介质时，部分能量转化为热能，导致光衰减，且与距离成指数关系；记为 κ \\kappa κ。

n n n和 κ \\kappa κ都与波长相关。二者组合为一个复数 n + i κ n+i\\kappa n+iκ，成为复数折射率。

非均匀介质可以看作内部有散射粒子的均匀介质。

散射和吸收都是尺度相关的（scale-dependent）。

通常情况下，散射和吸收合起来决定了介质的外观。

1.3 表面

影响光波碰撞表面效果的两方面因素：表面两侧的物质和表面的几何特征。

物质特征方面

表面分割不同折射率的物质，导致了空间不连续，使得光以特殊形式散射。而边界条件需要又要求平行于表面的电场分量必须是连续的；即两侧的电场向量在表面上的投影必须匹配。这有以下几个影响：

  1. 在表面处，任何散射波必须与入射波同相，或 18 0 ο ⁡ 180^\\operatorname\\omicron 180ο的异相。这限制了散射波只能有两个方向，一个继续向表面内部，一个则离开表面；分别为投射波（transmitted wave）和反射波（reflected wave）；
  2. 散射波必须和入射波的频率相同；
  3. 相位速度的变化与相对折射率（ n 1 / n 2 n_1/n_2 n1​/n2​）成正比。因频率不变，则波长变化与（ n 1 / n 2 n_1/n_2 n1​/n2​）成正比。

反射波方向与表面法线的夹角等于入射波方向与法线的夹角（ θ i \\theta_i θi​）；投射波方向 θ t \\theta_t θt​与入射波关系： sin ⁡ ( θ t ) = n 1 n 2 sin ⁡ ( θ i ) \\sin(\\theta_t)=\\cfracn_1n_2\\sin(\\theta_i) sin(θt​)=n2​n1​​sin(θi​)，折射定律，又叫斯涅尔定律（Snell’s law）。

不透明介质的折射：光线会在物体内部经历散射和吸收。

金属介质：内部自由电子吸收掉光能量，并将其重新发射到发射方向。所以金属有高吸收率和高反射率的特性。

渐变的折射率可以产生如热气蒸腾的效果。

折射率不变的情况下，不会产生折射和反射现象。

几何特征方面

表面不可能绝对平坦。但是远远小于光波长的不规则度，不会对光产生影响；远远大于光波长的不规则性，则不会改变局部的平整度。只有1到100个波长尺度的不规则度，可以产生明显不同于平面的现象，称为衍射（diffraction）。

在渲染领域，通常会采用几何光学（geometrical optics），忽略光的波动性，如干涉、衍射等；即假设表面的不规则度远远小于或大于光波长。几何光学将光看作是射线，而不是波。

微几何（microgeometry）：远大于光波长的不规则度，会改变表面方向；但是其尺寸对于单独渲染又太小。每个像素覆盖了法线方向不同的点，其外观则由不同反射方向的聚合结果生成。

在渲染领域，使用微结构法线的随机分布来表示微几何。反射光和折射光可以建模为方向的连续分布。

1.4 次表面（subsurface）散射

次表面散射光离开表面的位置与入射光位置有不同的距离。入射出射点距离分布取决于材质内散射粒子的密度和属性。

如果入射出射点距离小于着色尺度，那么可以将次表面散射合并到一个局部着色模型。次表面散射光外观与表面反射光有很大不同，所以将其分为几个单独的着色项比较容易处理：

  • 高光项（specular term）：表示表面反射；
  • 漫反射项（diffuse term）：表示局部次表面散射；

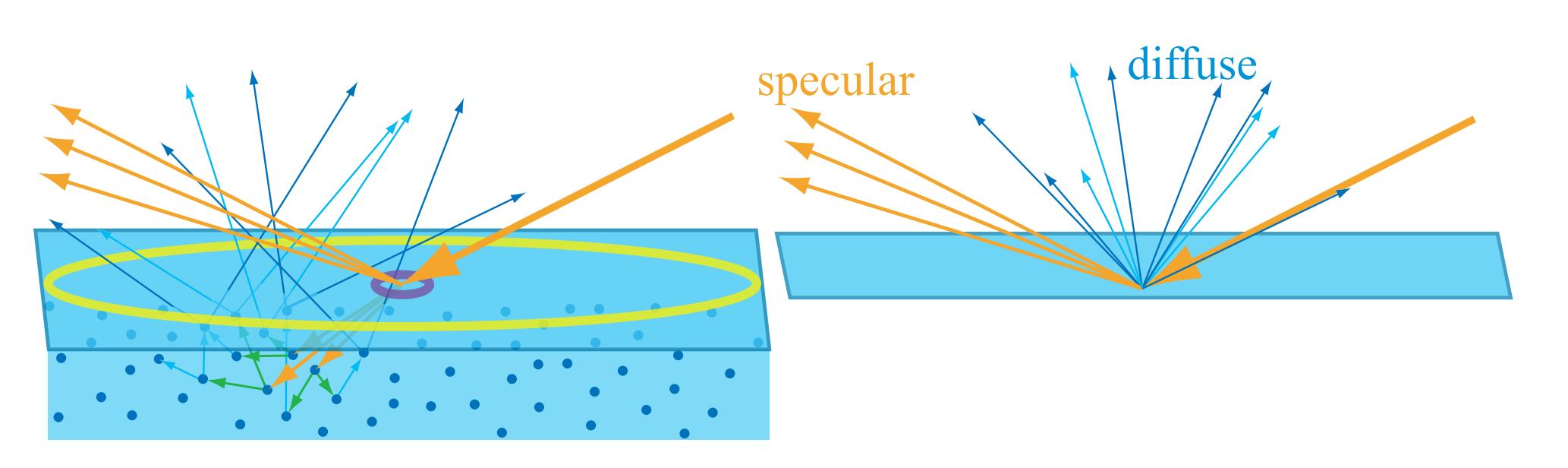
如果入射出射点距离大于着色尺度，需要使用全局次表面散射（global subsurface scattering）技术。

局部和全局次表面区别如下图所示：

二、相机

相机系统的组成：

  • 一个传感器平面，其由很多独立的小传感器。每个传感器可以探测到其表面的辐照度，并产生一个颜色信号；
  • 带有一个小孔的遮光板，用于限制光线进入方向；
  • 置于小孔处的透镜，用于聚焦光线，使每个传感器只接收到一小股方向传来的光线；

传感器在系统内最终测量的其实是平均辐射率（radiance），用于量化一个单独光线的亮度和颜色。

渲染模拟的是一个非常简单的图像传感器，针孔相机。

在渲染时，每个着色样本都与一个单独光线相关，也就是传感器表面上的一个采样点。

在实际应用中，针孔相机模型很难实现；一般会使用透镜，即在一个更大的孔上安装透镜，这样可以极大的提高光量；不过这也引入了深度场限制，即太远或太近的物体会模糊。

三、BRDF

基于物理的渲染最终计算的是沿着视角射线进入相机的辐射率，记为 L i ( c , − v ) L_i(\\mathbf c,-\\mathbf v) Li​(c,−v)，其中 c \\mathbf c c是相机位置， − v -\\mathbf v −v是沿着视角射线的方向。

此处假设介质不对光线产生影响，那么进入相机的辐射率，等于最近的物体表面朝向相机发射的辐射率： L i ( c , − v ) = L o ( p , v ) L_i(\\mathbf c,-\\mathbf v)=L_o(\\mathbf p,\\mathbf v) Li​(c,−v)=Lo​(p,v)，其中 p \\mathbf p p是视线与最近物体表面的交点。根据该公式，计算目标改为 L o ( p , v ) L_o(\\mathbf p,\\mathbf v) Lo​(p,v)。

表面自身可以直接发光；也可能来源于其他地方发射来的光，并且反射到视线方向。表面反射、局部次表面反射只依赖于入射光方向 l \\mathbf l l，和出射向视线的方向 v \\mathbf v v。局部反射率通过双向反射分布函数（bidirectional reflectance distribution function，BRDF），记为 f ( l , v ) f(\\mathbf l,\\mathbf v) f(l,v)。

BRDF用于定义均匀表面，即表面上所有点的BRDF都一样。但在现实世界中，很少有均匀表面。技术上来讲，基于空间位置测量的BRDF变化函数，称为空间变换的BRDF（spatially varying BRDF，SVBRDF）或空间BRDF（spatial BRDF，SBRDF）。

入射和出射方向都有两个自由度。参数化表示为两个角：相对于法线的仰角 θ \\theta θ和围绕法线的水平角 ϕ \\phi ϕ。一般来说，BRDF是四个变量的函数；但是对于各向同性的BRDF来说，在保持入射和出射方向的相对夹角不变的情况下，围绕法线旋转不会改变BRDF。那么各向同性的BRDF就是有三个参数的函数，其中光线和视线的旋转夹角需要考虑。


不考虑荧光和磷光，所以反射光的波长与入射光相同。反射光的量由波长决定，这可以有两种表示方式：1.将波长作为BRDF的参数，这一般在离线渲染中使用；2.将BRDF表示为光谱分布值，实时渲染一般采用这种方式。

将BRDF引入反射方程（reflectance equation）：
L o ( p , v ) = ∫ l ∈ Ω f ( l , v ) L i ( p , l ) ( n ⋅ l ) d l L_o(\\mathbf p,\\mathbf v)=\\int_\\mathbf l \\in \\Omegaf(\\mathbf l,\\mathbf v)L_i(\\mathbf p,\\mathbf l)(\\mathbf n \\cdot \\mathbf l)d\\mathbf l Lo​(p,v)=∫l∈Ω​f(l,v)Li​(p,l)(n⋅l)dl

其中， l ∈ Ω \\mathbf l \\in \\Omega l∈Ω表示是在表面上方的单位半球面进行积分的。说明人意入射方向都会产生相应的出射辐射率。

为了简洁起见，表示表面位置的 p \\mathbf p p可以忽略掉：
L o ( v ) = ∫ l ∈ Ω f ( l , v ) L i ( l ) ( n ⋅ l ) d l L_o(\\mathbf v)=\\int_\\mathbf l \\in \\Omegaf(\\mathbf l,\\mathbf v)L_i(\\mathbf l)(\\mathbf n\\cdot\\mathbf l)d\\mathbf l Lo​(v)=∫l∈Ω​f(l,v)Li​(l)(n⋅l)dl

当计算反射方程时，半球经常参数化为 ϕ \\phi ϕ和 θ \\theta θ，则可以表示为：
L o ( θ o , ϕ o ) = ∫ ϕ i = 0 2 π ∫ θ i = 0 π / 2 f ( θ i , ϕ i , θ o , ϕ o ) L ( θ i , ϕ i ) cos ⁡ θ i sin ⁡ θ i d θ i d ϕ i L_o(\\theta_o,\\phi_o)=\\int_\\phi_i=0^2\\pi\\int_\\theta_i=0^\\pi/2f(\\theta_i,\\phi_i,\\theta_o,\\phi_o)L(\\theta_i,\\phi_i)\\cos\\theta_i\\sin\\theta_id\\theta_id\\phi_i Lo​(θo​,ϕo​)=∫ϕi​=02π​∫θi​=0π/2​f(θi​,ϕi​,《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading

《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading

《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 2 The Graphics Rendering Pipeline