区间DP入门

Posted 2020-11-28 accepting

例题： LeetCode 5 最长回文子串   LeetCode  516 最长回文子序列  Acwing 石子归并

最长回文子串：

　　定义状态dp[i][j]表示区间i~j是一段回文串，如果dp[i][j]是回文串的话，s[i]=s[j]并且dp[i-1][j-1]（i != j）是个回文串，所以说转台转移方程就是

　　dp[i][j]=1(当dp[i-1][j-1]==1&&s[i]==s[j])

　　code：

　　

class Solution {
    bool dp[1000+7][1000+7];
public:
    string longestPalindrome(string s) {
        int n=s.size();
        for(int i=1;i<=n;i++) dp[i][i]=1;
        for(int i=1;i<n;i++){
            if(s[i-1]==s[i]){
                dp[i][i+1]=1;
            }
        }
        for(int len=3;len<=n;len++){
            for(int l=1,r=len;r<=n;l++,r++){
                if(s[l-1]==s[r-1]&&dp[l+1][r-1]){
                    dp[l][r]=1;
                }
            }
        }
        string ans="";
        int i=-1,j=-1;
        int len=0;
        for(int l=1;l<=n;l++){
            for(int r=l;r<=n;r++){
                if((r-l+1)>len&&dp[l][r]){
                    i=l;j=r;
                    len=r-l+1;
                }
            }
        }
        if(i!=-1) for(int k=i;k<=j;k++) ans+=s[k-1];
        return ans;
    }
};

LeetCode  516 最长回文子序列　

　　

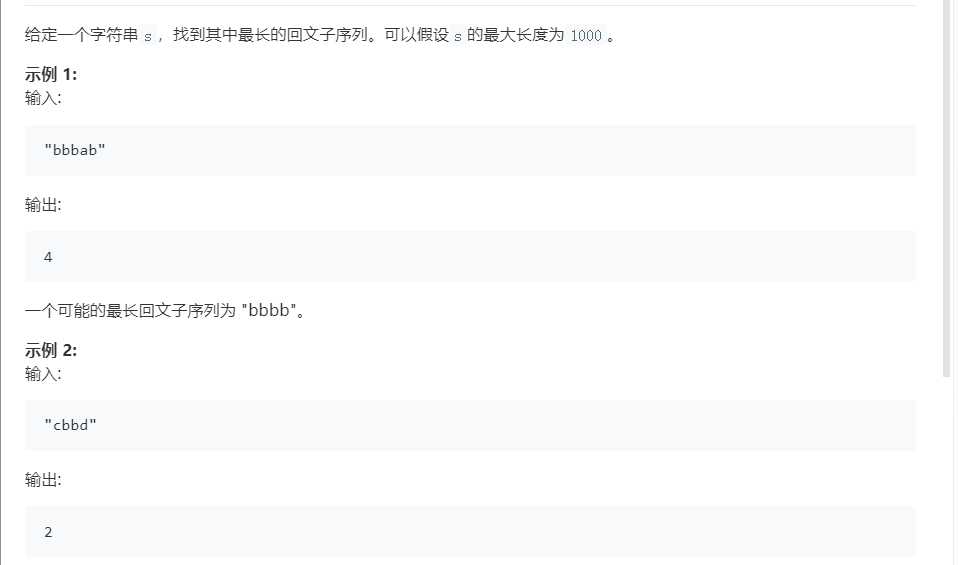
 题解：定义状态dp[l][r]表示区间[l,r]之间的回文串的最大长度。

　　怎么转移的的？dp[l][r]可以由dp[l][r-1]或者d[l+1][r]转移过来，当s[l]==s[r]的时候dp[l][r]也可以有dp[l+1][r-1]转移过来。

　　code:

　　

class Solution {
    int dp[1000+7][1000+7];
public:
    int longestPalindromeSubseq(string s) {
        int n=s.size();1
        for(int i=1;i<=n;i++) dp[i][i]=1;
        for(int i=1;i<n;i++){
            dp[i][i+1]=1;
            if(s[i-1]==s[i])
              dp[i][i+1]=2;
        }
        for(int len=3;len<=n;len++){
            for(int l=1,r=len;r<=n;l++,r++){
                dp[l][r]=max(dp[l+1][r],dp[l][r-1]);
                if(s[l-1]==s[r-1]){
                    dp[l][r]=max(dp[l][r],dp[l+1][r-1]+2);
                }
            }
        }
        return dp[1][n];
    }
};

Acwing 282. 石子合并

题面：

 

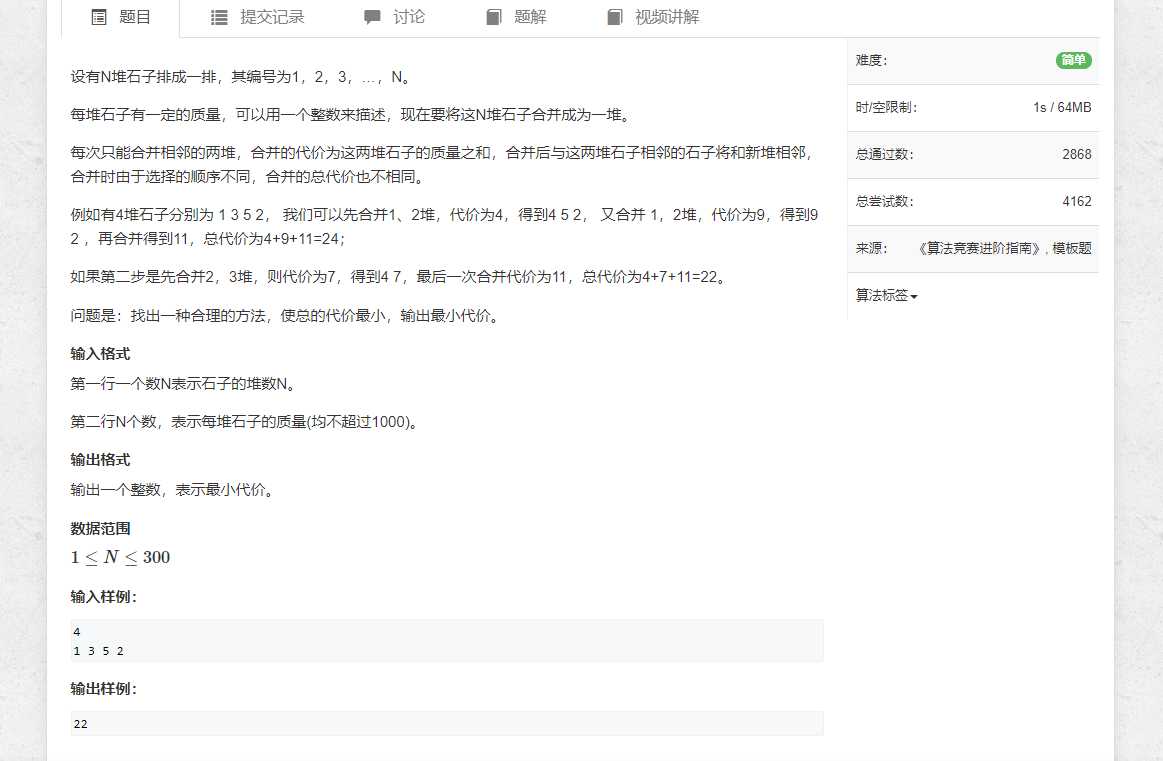
 题解：定义状态dp[l][r]表示合并区间l~r需要的最小代价，该怎么转移呢？

 

 

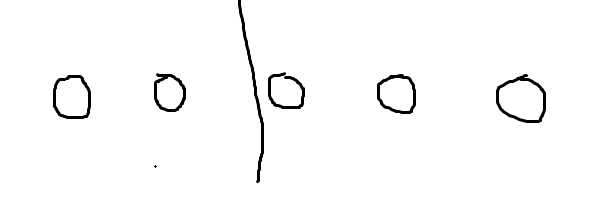
假设有5个石头，dp[1][5]，我们可以将1~5拆分成1~2和3~5，或者1~1和2~5等等....所以状态转移方程为dp[l][r]=dp[l][i]+dp[i+1][r]+sum[l,r]，l<=i&&i+1<=r。sum就是区间和，可以将前缀和预处理出来

 

#include<bits/stdc++.h>
using namespace std;
const int N=300+7;
const int inf=1e9+7;
int dp[N][N];
int arr[N];
int sum[N];
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)
            dp[i][j]=inf;
    }
    for(int i=1;i<=n;i++){
        cin>>arr[i];
        sum[i]=sum[i-1]+arr[i];
        dp[i][i]=0;
    }
    for(int len=2;len<=n;len++){
        for(int l=1,r=len;r<=n;r++,l++){
            for(int i=l;i<r;i++){
                dp[l][r]=min(dp[l][r],dp[l][i]+dp[i+1][r]+sum[r]-sum[l-1]); 
            }
        }
    }
    cout<<dp[1][n]<<endl;
    return 0;
}