机器学习之朴素贝叶斯
Posted stephen-goodboy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习之朴素贝叶斯相关的知识,希望对你有一定的参考价值。
1、贝叶斯公式
贝叶斯的公式如下
[ P(B_{i}| A) = frac {P(B_{i} | P(A)) * P(B_{i})} { sum
olimits_{j=1}^{N} P(B_{j}) * P(A|P(B_{j}))}
]
2、分类中的朴素贝叶斯
上述公式中我们可以将A当做将要预测的实例,(B_{i})表示第(i)个类别标签,也就是说我们输入一个实例,得到在每一个类别标签上的概率,哪个大就选择哪个。
假设我们的训练数据集是
[ T = {(x_{1},y_{1}),(x_{2},y_{2})........(x_{N},y_{N})}
]
由这个训练数据集,我们可以算出每个类别标签在整个数据集出现的概率
[ P(Y|c_{k}) , k = 1,2,3 ....k
]
我们可以得到实例中每个实例所对应的条件概率表示
[ P(X=x|Y=c_{k}) = P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)}.....X^{(n)}=x^{(n)} | Y = c_{k})
]
由于(P(X=x|Y=c_{k}))有指数数量的参数,所以在求解时是不符合实际需要的,所以在这里我们做了个假设,就是各个(x^{1},x^{2}....x^{n})之间是相互独立的,这也是为什么这种算法叫朴素贝叶斯的原因,最终(P(X=x|Y=c_{k}))可以表示成如下:
[ P(X=x|Y=c_{k}) = prod_{j=1}^{n} P(X=x^{j} | Y=c_{k})
]
根据数据集,我们可以求解以上的一些参数,当这些参数求解之后,我们就可以进行预测新的实例了。假设我们有一条新的实例x,如何预测其分类的结果呢?首先我们根据贝叶斯公式可以得到
[ P(Y = y_{k} | X = x )
]
即我们得到所有类别的概率,并选择最大的概率的类别作为结果。展开后为
[ P(Y = y_{k} | X = x ) = frac {P(Y = y_{k}) * P(X=x |Y = y_{k})} {sum
olimits_{k} P(X=x |Y = y_{k})P(Y=y_{k})}
]
由于我们的前提假设,各个(x^{l})之间是相互独立的,所以可以写成
[ P(Y = y_{k} | X = x ) = frac { P(Y = y_{k}) * prod_{j} P(X^{(j)} = x^{(j)} | Y = y_{k}) } {sum
olimits_{k} P(Y=y_{k}) * prod_{j} P(X^{(j)} = x^{(j)} | Y = y_{k}) }
]
接下来我们要计算(P(Y = y_{k} | X = x ))所对应的类别,即
[ y = argmax_{y_{k}} P(Y = y_{k} | X = x )
]
由于式子中分母都相同,所以我们只需要最大化分子即可
[ y = argmax_{y_{k}} P(Y = y_{k}) * prod_{j} P(X^{(j)} = x^{(j)} | Y = y_{k})
]
3、一个例子
这里我们就copy一下《统计学习方法》上的例子了,上面已经讲得很清楚了,我感觉自己举的例子也不一定有这个清楚。
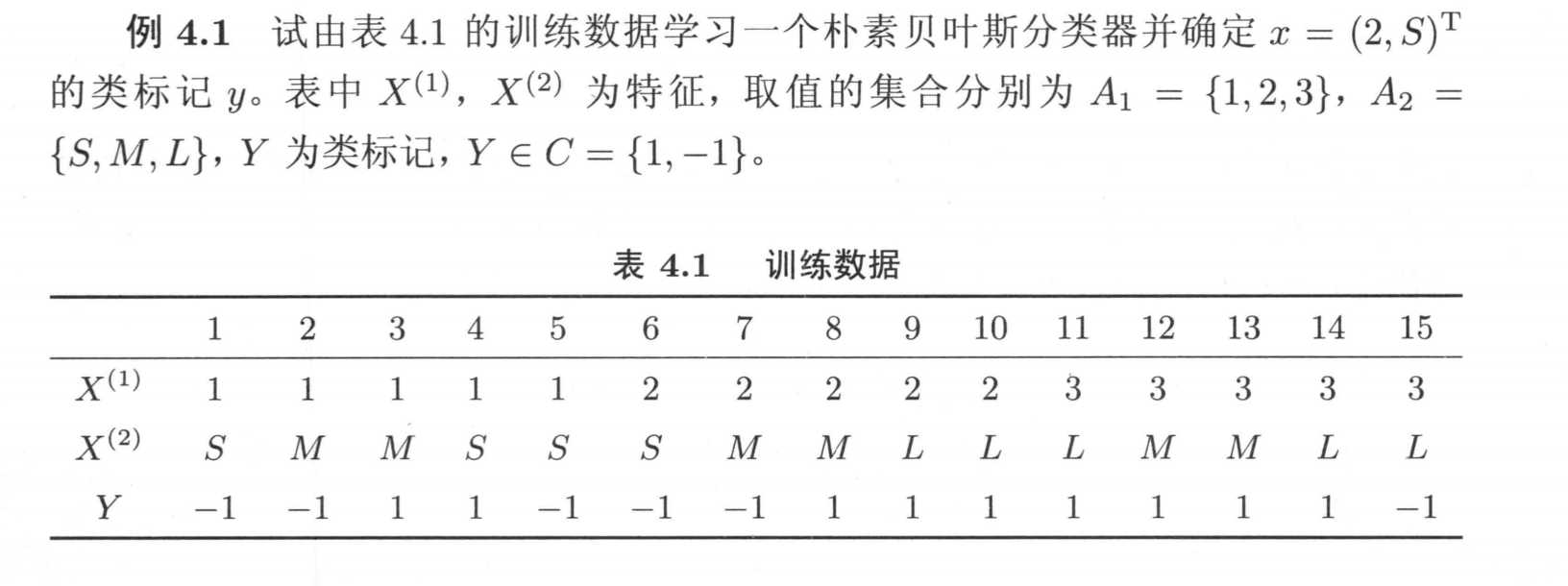
根据公式得到下面的概率
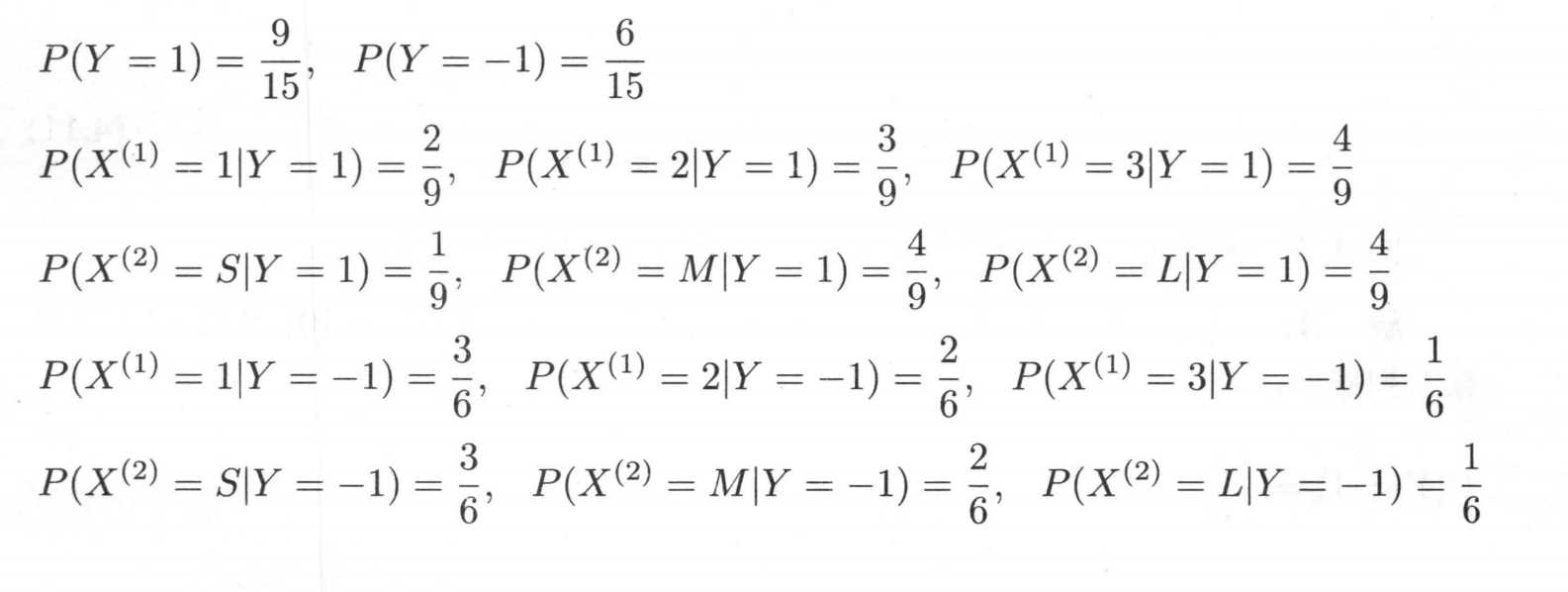
最后我们选择最大的类别作为最终的类别
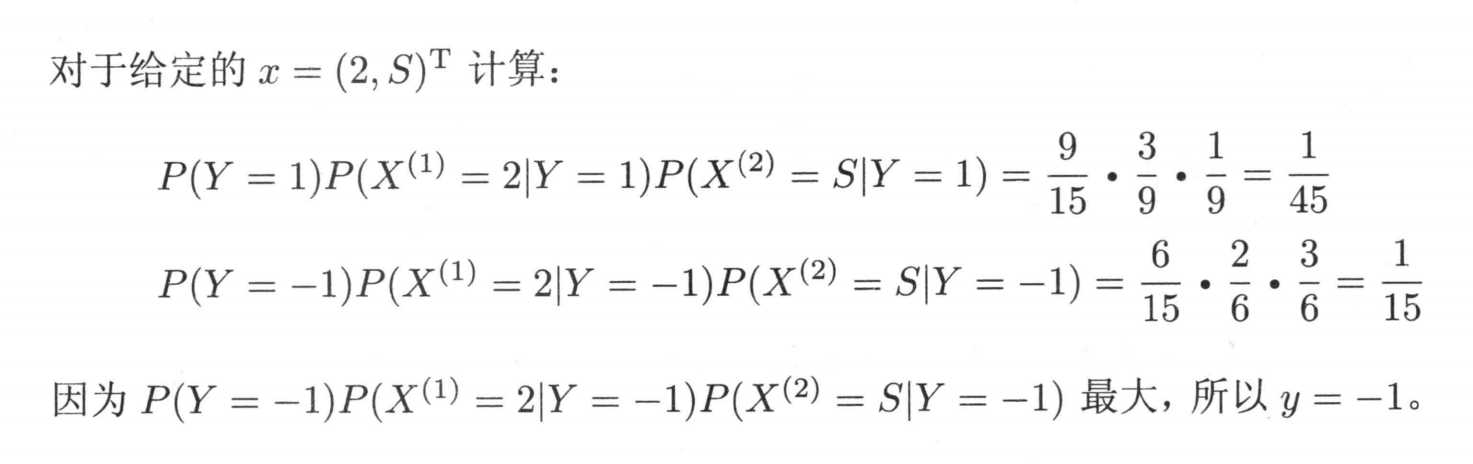
以上是关于机器学习之朴素贝叶斯的主要内容,如果未能解决你的问题,请参考以下文章