图论之二分图

Posted 2020-11-28 mgtnb

一、二分图定义

设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

即二分图上的每条边的两个顶点在不同集合中

                                         

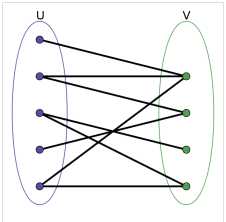
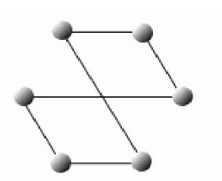
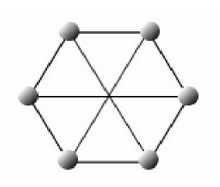
如上图都为二分图

                 

 

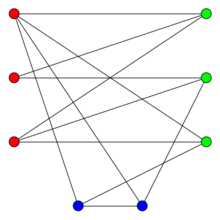
而上图则不是一个二分图

二分图定理：

二分图中不存在奇环，只存在偶环。

二分图判定：

染色法：把一个顶点染成黑色，与之相邻的顶点染成白色，若染色过程中发现相邻点已染色且颜色相同，则不是一个二分图（即找到了一个奇环）

二、匹配

匹配：设M为二分图G的一个子集，若M中任意两条边都没有公共顶点，则M称为G的一个子集

最大匹配：所有匹配中含边数最多的一个

完全匹配：图中每个点都包含在内的一个匹配

完全匹配一定是最大匹配，但最大匹配不一定是完全匹配

每个图都有自己的最大匹配，但不是每个图都有完全匹配

完备匹配：一个二分图中，两集合点数量都为n，且最大匹配边数也为n

 

匈牙利算法求最大匹配

交错路径：给定图G的一个匹配M，如果一条路径的边交替出现在M中和不出现在M中，我们称之为一条M-交错路径。

增广路径：M-交错路径中的两个端点都不与M中的边关联，则称之为M-增广路径

当前我们找到的匹配M，在增广路径中明显存在一个比它大一的匹配，所以就找到了更大的匹配

所以，匈牙利算法的核心思想就是不断找到增广路径来更新当前更大的匹配

当再也找不到增广路径时，即找到了最大匹配

 

如何找到一条増广路：

对于x寻找的匹配点y有两种情况可以将它们匹配：

1.y本身还没有匹配，x、y相连    此时，（x,y）构成了一条长度为1的増广路

2.y已经和x‘匹配，但x‘能够找到一个y‘与之匹配    此时，x~y~x‘~y‘为一条増广路

举个例子：

                               

 

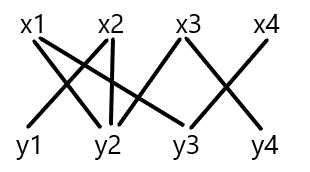
对于上图，从点x1开始，找到y2与之匹配，然后x2找到y1与之匹配

                             

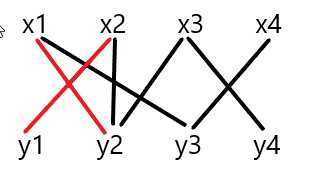
再x3，因为y2已经与x1匹配，但x1可以与y3匹配     所以对于现在的匹配边（x1,y2）找到了一条増广路 x3~y2~x1~y3，

                                

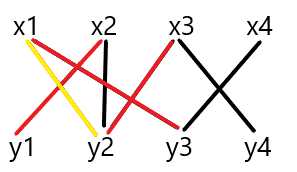
再x4，到y3，x1就到y2，所以x3就到y4     所以对于现在的匹配边，（x1,y3）及（x3,y2）找到了一条増广路 x4~y3~x1~y2~x3~y4

                               

 

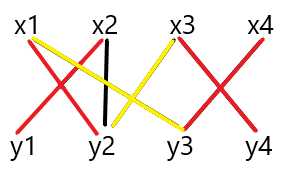
 此时这个图的最大匹配就找到了

bool dfs(int x)
{
    for (int i = head[x]; i; i = next[i])
    {
        int y = ver[i];
        if (!vis[y])
        {
            vis[y] = 1;
            if (!match[y] || dfs(match[y]))
            {
                match[y] = x;
                return 1;
            }
        }
    }
    return 0;
}

for (int i = 1; i <= n; i++)
{
    memset(vis, 0, sizeof(vis));
    if (dfs(i)) ans++;
}

匈牙利算法

 

KM算法求带权最大匹配

带权最大匹配（即最优匹配）：每条边带有一个权值，在最大匹配中，边权值总和最大的一种匹配

交错树：匈牙利算法中，如果从某个点出发寻找匹配失败，则所有此次访问过的点共同构成一棵树

顶标：即“顶点标记值”   在二分图中，给左部点i一个整数值ai，右部点j一个整数值bj

           其中必须满足任意ai+bj>=w[i][j]    w[i][j]为i、j两点的边权值

           这些整数值则称为节点的顶标

相等子图：二分图中所有满足ai+bj=w[i][j]的边构成的子图

定理：

          若在相等子图中存在完备匹配，则这个完备匹配则为二分图的带权最大匹配

 

KM算法的核心思想利用的便是上定理

https://www.cnblogs.com/wenruo/p/5264235.html

详见上博客，便于理解

 

对于上博客中，每个男女生的期望值，就是这个点的顶标

每次为女生找对象失败，就是相当于找到了一个交错树

判定可以配对的条件就是相等子图的条件

const int N = 105;
int w[N][N]; 
int la[N], lb[N];
bool va[N], vb[N]; 
int match[N];
int n, d, u[N];
bool dfs(int x)
{
    va[x] = 1;
    for (int y = 1; y <= n; y++)
    {
        if (!vb[y])
        {
            if (la[x] + lb[y] - w[x][y] == 0)
            {
                vb[y] = 1;
                if (!match[y] || dfs(match[y]))
                {
                    match[y] = x;
                    return 1;
                }
            }
        }
        else u[y] = min (u[y], la[x] + lb[y] - w[x][y]);
    }
    return 0;
}

int KM()
{
    for (int i = 1; i <= n; i++)
    {
        la[i] = -(1<<30);
        lb[i] = 0;
        for (int j = 1; j <= n; j++)
            la[i] = max (la[i], w[i][j]);
    }
    for (int i = 1; i <= n; i++)
    {
        while(1)
        {
            memset(va, 0, sizeof(va));
            memset(vb, 0, sizeof(vb));
            for (int j = 1; j <= n; j++)
                u[j]=1e10;
            if (dfs(i)) break;
            for (int j = 1; j <= n; j++)
                if (!vb[j]) d = min(d, u[j]);
            for (int j = 1; j <= n; j++)
            {
                if (va[j]) la[j] -= d;
                if (vb[j]) lb[j] += d;
            }
        }
    }
    int ans=0;
    for (int i = 1; i <= n; i++)
        ans += w[match[i]][i];
    return ans;
}

KM

 

---

 

 

题目

关押罪犯

https://www.luogu.com.cn/problem/P1525

二分+二分图判定

#include<bits/stdc++.h>
using namespace std;

const int MAX=200002; 

int n,m;
int head[MAX],nex[MAX],ver[MAX],w[MAX],tot;
int vis[MAX];

void add(int x,int y,int z)
{
    w[tot]=z,ver[tot]=y,nex[tot]=head[x],head[x]=tot++;
}

bool dfs(int x,int c,int midd)
{
    vis[x]=c;
    for(int i=head[x];i;i=nex[i])
    {
        int y=ver[i];
        if(w[i]<=midd) continue;
        if(vis[y]==0)
        {
            if(dfs(y,3-c,midd)==0) return 0;
        }
        else if(vis[y]==c) return 0;
    }
    return 1;
}

bool check(int midd)
{
    memset(vis,0,sizeof(vis));
    for(int i=0;i<n;i++)
        if(!vis[i]) 
            if(!dfs(i,1,midd)) return 0;
    return 1;
}

int main()
{
    scanf("%d%d",&n,&m);
    int maxx=0;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        maxx=max(maxx,z);
        add(x,y,z);
        add(y,x,z);
    }
    int l=0,r=maxx+1;
    while(l<r)
    {
        int midd=(l+r)>>1;
        if(check(midd)) r=midd;
        else l=midd+1;
    }
    printf("%d",r);
    return 0;
}

关押罪犯

 

酒店之王

https://www.luogu.com.cn/problem/P1402

建立两个二分图，同时求二分图的最大匹配，综合得到答案

注意点在于，如果当前没办法再找到增光路，就回到前一个状态

#include<bits/stdc++.h>
using namespace std;

const int N=105;

int n,p,q;
int r[N][N],f[N][N];
int nr[N],nf[N],used[N]; 
int lr[N],lf[N],las[N];
bool vr[N],vf[N];

int room(int x)
{
    for(int i=1;i<=p;i++)
    if(!vr[i]&&r[x][i])
    {
        vr[i]=1;
        if(!nr[i]||room(nr[i]))
        {
            nr[i]=x;
            return 1;
        }
    }
    return 0;
}

int food(int x)
{
    for(int i=1;i<=q;i++)
    if(!vf[i]&&f[x][i])
    {
        vf[i]=1;
        if(!nf[i]||food(nf[i]))
        {
            nf[i]=x;
            return 1;
        }
    }
    return 0;
}

int main()
{
    scanf("%d%d%d",&n,&p,&q);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=p;j++)  
            cin>>r[i][j];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=q;j++)  
            cin>>f[i][j];
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        memset(vr,0,sizeof(vr));
        memset(vf,0,sizeof(vf));
        for(int j=1;j<=n;j++) 
            lr[j]=nr[j],lf[j]=nf[j];
        if(room(i)&&food(i)) ans++;
        else  
        {
            for(int j=1;j<=n;j++)
                nr[j]=lr[j],nf[j]=lf[j];
        }
    }
    cout<<ans<<endl;
    return 0;
}

酒店之王