CodeChef Tree Palindromes

Posted 2020-11-28 autoint

Tree Palindromes

Given a tree rooted at node 1 with N nodes, each is assigned a lower case latin character. Print the sum of length of longest palindrome substring from string generated by simple path from root to all other nodes i.e root to some other node (say x) will represent a string, find its lps length and add it to answer for all such nodes x. Then print final answer.

1 ≤ N ≤ 10⁵

题解

翁文涛《回文树及其应用》。

回文树也可以有类似AC自动机的不全转移，不过这个补全是间接性的。

(t=even) 的时候要特殊处理。考虑实际意义（或者get_fail过程）可知 (quick_{even}[c]=odd)。

有了这个Trie上就好做了。

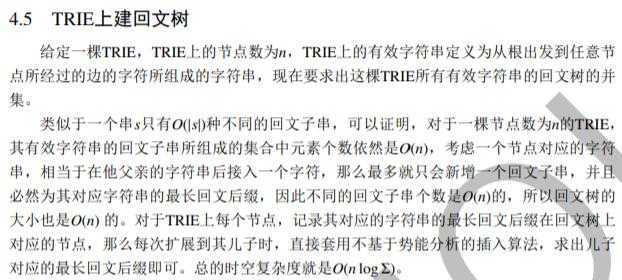
本题字符集较小，在插入的时候，没有必要将失配转移可持久化，直接开一个数组记录即可。时间复杂度 (O(nSigma))。

CO int N=100000+10;
vector<int> to[N];

namespace PAM{
    int str[N],n;
    int tot;
    int ch[N][26],trans[N][26],fa[N],len[N];
    
    IN void init(){
        memset(str,-1,sizeof str);
        tot=1;
        fa[0]=fa[1]=1;
        len[0]=0,len[1]=-1;
        fill(trans[0],trans[0]+26,1);
    }
    int extend(int p,int c){
        if(str[n-len[p]-1]!=str[n]) p=trans[p][c];
        if(!ch[p][c]){
            int cur=++tot;
            len[cur]=len[p]+2;
            fa[cur]=ch[trans[p][c]][c];
            ch[p][c]=cur;
            copy(trans[fa[cur]],trans[fa[cur]]+26,trans[cur]);
            trans[cur][str[n-len[fa[cur]]]]=fa[cur];
        }
        return ch[p][c];
    }
}

char tree[N];
int last[N],res[N];
LL ans;

void dfs(int x,int fa){
    PAM::str[++PAM::n]=tree[x]-'a';
    last[x]=PAM::extend(last[fa],tree[x]-'a');
    res[x]=max(res[fa],PAM::len[last[x]]);
    ans+=res[x];
    for(int i=0;i<(int)to[x].size();++i)
        if(to[x][i]!=fa) dfs(to[x][i],x);
    --PAM::n;
}
int main(){
    int n=read<int>();
    scanf("%s",tree+1);
    for(int i=1;i<n;++i){
        int u=read<int>(),v=read<int>();
        to[u].push_back(v),to[v].push_back(u);
    }
    PAM::init();
    dfs(1,0);
    printf("%lld
",ans);
    return 0;
}