关于主定理的几点注记

Posted 2020-11-28 zyna

1、主定理并不能包含所有的递推情况，例如对于T(N) = 2T(N/2) + NlogN就没有落入主定理当中，需要采用递推树求解

2、主定理的第三种情况可以看成两个条件：1）f(N) = Ω(n^(logb(a) + e))，其中e>0对于充分大的成立，2）存在1 >c > 0，使得对于充分大的N，有af(N/b) <= cf(N)。我们可以证明，实际上条件2蕴涵了条件1，那么问题是是否存在满足1）但是不满足2）的f使得主定理的第三种情况不成立呢？答案是肯定的，考虑f(n) = n*(2-cos(n))，只是作为一个数学上的小问题了，不太可能成为复杂度的。

3、在算法导论中有一个思考题：

 

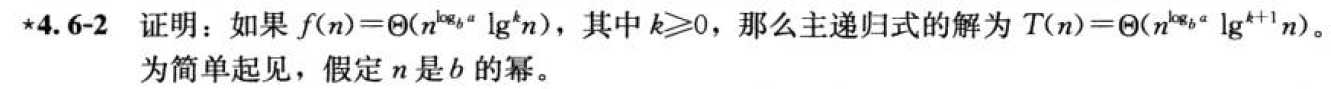
 推导的前面步骤和第二种情况一模一样，只是最后需要用到一个高数的结果：(1^p + 2^p + ... + n^p)/n^(p+1)次对p>0的n存在极限1/(p+1)，具体的推到交给读者，我们给出链接：

https://www.zhihu.com/question/28541195?sort=created