递归和分治思想

Posted 2020-11-28 lemonzhang

1、递归：（归去来兮）

递归效率较低，如果明确知道迭代次数，则能用迭代最好用迭代，递归是函数自己调用自身，每次调用都需要入栈等操作。但是递归操作要比迭代简单和清楚。

2、斐波那契数列的递归实现

#include <stdio.h>
int Fib(int i);
int main()
{
    int i;
    printf_s("请输入一个大于零的整数
");
    scanf_s("%d", &i);
    for (; i >= 0; i--)
    {
        printf_s("%d ", Fib(i));
    }
    
    return 0;
}

int Fib(int i)
{
    if (i < 2)
        return i == 0 ? 0 : 1;
    return Fib(i - 1) + Fib(i - 2);
}

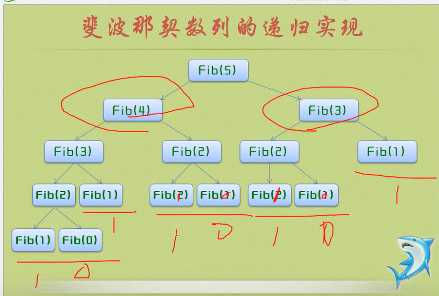
1）递归定义至少有一个终止条件，函数不再调用自身，开始返回。

2）递归和迭代的区别：迭代使用的是循环结构，递归使用的是选择结构。但大量的递归调用会建立函数的副本，会消耗大量的时间和内存，而迭代不需要这种付出。

3）递归函数分为调用阶段和回退阶段，递归的回退顺序是它调用顺序的逆序。

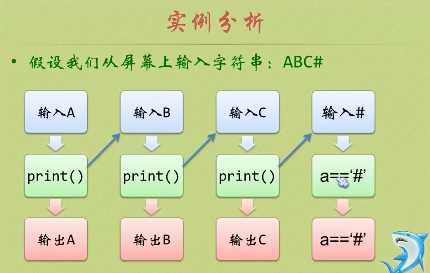
举例：打印输入字符的倒序输出：

void print()
{
    char a;
    scanf_s("%c", &a);
    if (a != ‘#‘) print();
    if (a != ‘#‘) printf_s("%c", a);
}

3、分治思想

采取各个击破，分而治之的原则。当一个问题规模较大且不容易求解时，可以考虑将其分为几个小的模块，逐一解决。采用分治思想处理问题时，其各个小模块通常具有与大问题相同的结构。

4、折半查找

折半查找法，是一种常用的查找方法，该方法通过不断缩小一半查找的范围，直到达到目的，所以效率比较高

前提：针对有序数组（元素从小到大或从大到小），优点是查找速度比较快，时间复杂度为O(log₂n)。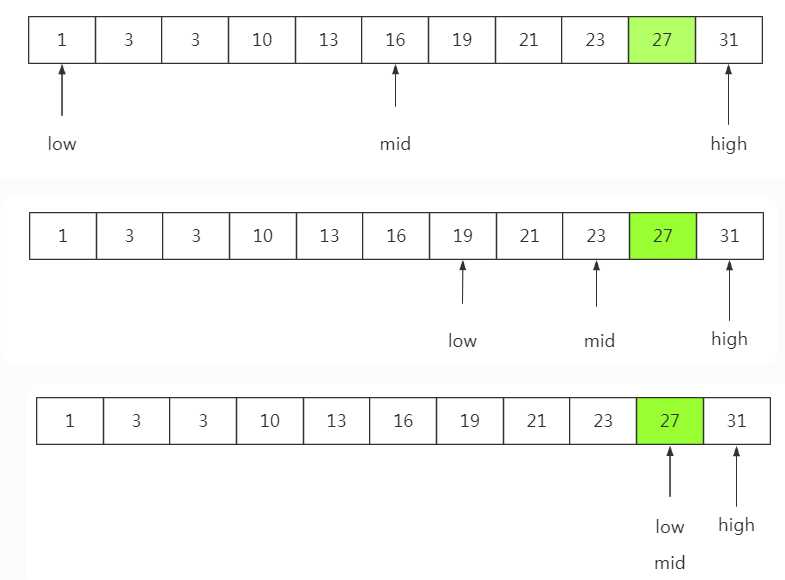

 迭代实现：

int main()
{
    int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 };
    int left, mid, right,num;
    left = 0;
    right = 10;
    num = 27;

    while (left <= right)
    {
        mid = (left + right) / 2;
        if (a[mid] > num)
            right = mid - 1;
        else if (a[mid] < num)
            left = mid + 1;
        else
            break;
    }
    printf("index:%d", mid);
    system("pause");
    return 0;
}

递归实现

int binary_search(int arr[], int left, int right,int ele)
{
    int mid = (left + right) / 2;
    if (arr[mid] > ele)
        right = mid - 1;
    else if (arr[mid] < ele)
        left = mid + 1;
    else
        return mid;
    return binary_search(arr, left, right, ele);
}

int main()
{
    int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 };
    int left, right, num, index;
    left = 0;
    right = 10;
    num = 27;

    index = binary_search(a, left, right, num);
    
    printf("index:%d", index);
    system("pause");
    return 0;
}