平衡二叉搜索树(AVL树,红黑树)数据结构和区别

Posted 2020-11-28 mrxiab

平衡二叉搜索树（Balanced Binary Search Tree）

经典常见的自平衡的二叉搜索树（Self-balancing Binary Search Tree）有

① AVL树 ：Windows NT 内核中广泛使用

② 红黑树：C++ STL（比如 map、set ）Java 的 TreeMap、TreeSet、HashMap、HashSet  Linux 的进程调度  Ngix 的 timer 管理

 

1 AVL树  vs  红黑树

①AVL树 平衡标准比较严格：每个左右子树的高度差不超过1

  最大高度是 1.44  ∗  log2  n + 2 − 1.328（100W个节点，AVL树最大树高28）

  搜索、添加、删除都是 O(logn) 复杂度，其中添加仅需 O(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整

② 红黑树 平衡标准比较宽松：没有一条路径会大于其他路径的2倍

  最大高度是 2 ∗ log2(n + 1)（ 100W个节点，红黑树最大树高40）

  搜索、添加、删除都是 O(logn) 复杂度，其中添加、删除都仅需 O(1) 次旋转调整

? 搜索的次数远远大于插入和删除，选择AVL树；搜索、插入、删除次数几乎差不多，选择红黑树

? 相对于AVL树来说，红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作，整体来说性能要优于AVL树

? 红黑树的平均统计性能优于AVL树，实际应用中更多选择使用红黑树

 

2 AVL和红黑树各自数据结构

 2.1 AVL树

 平衡因子（Balance Factor）：某结点的左右子树的高度差

 AVL树的特点:

 1) 每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为“失衡”）

 2) 每个节点的左右子树高度差不超过 1

 3) 搜索、添加、删除的时间复杂度是 O(logn)

 

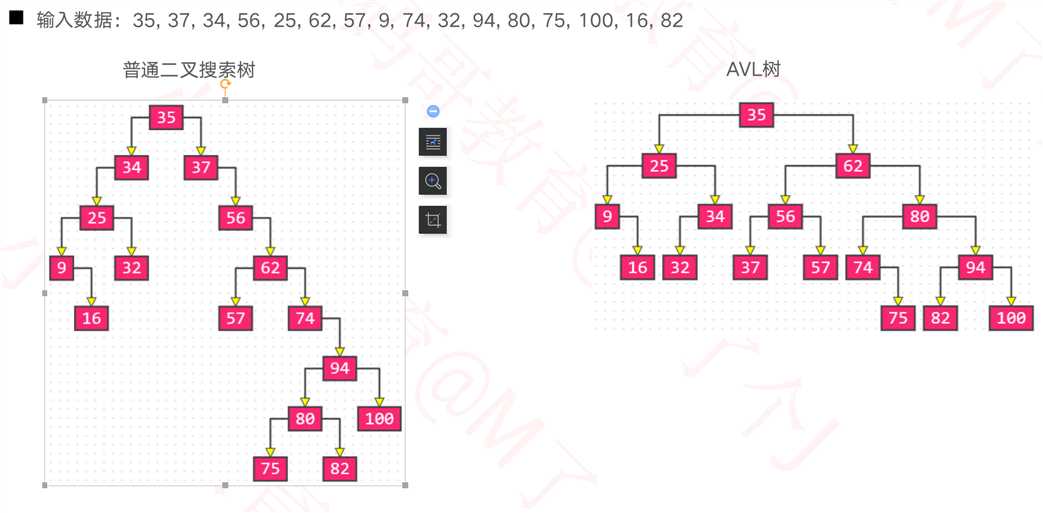
    2.1.1 添加导致的失衡

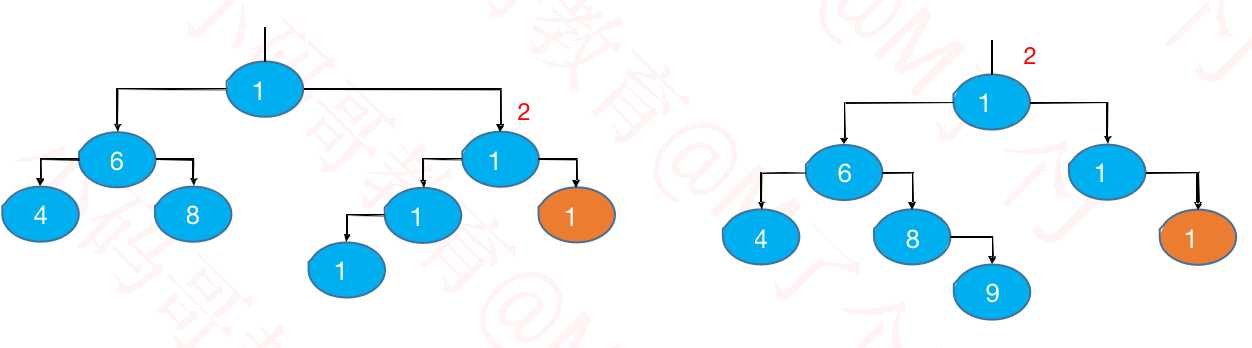
    ? 示例：往下面这棵子树中添加 13

    ? 最坏情况：可能会导致所有祖先节点都失衡

    ? 父节点、非祖先节点，都不可能失衡

    

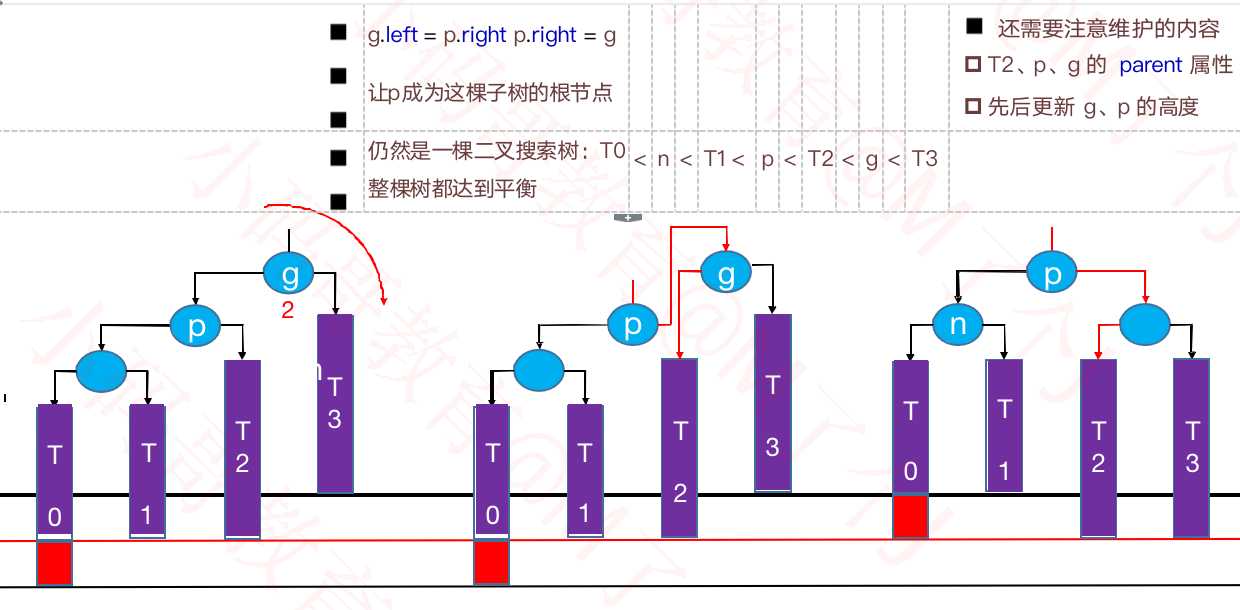
    ①LL – 右旋转（单旋）

    

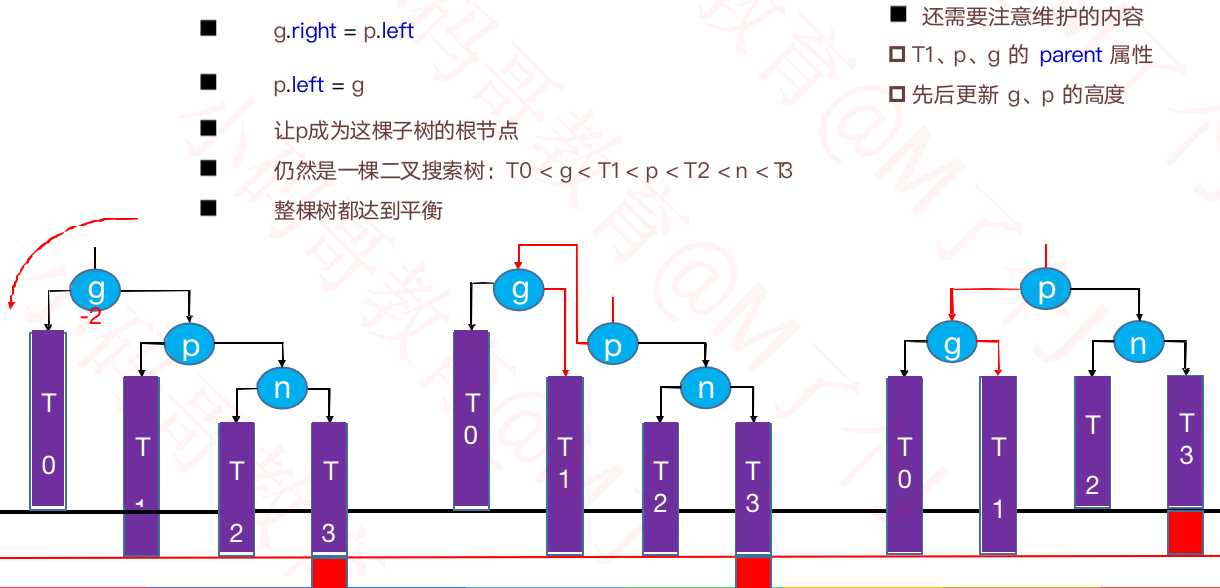
    ②RR – 左旋转（单旋）

    

 

    ③LR – RR左旋转，LL右旋转（双旋）

    

 

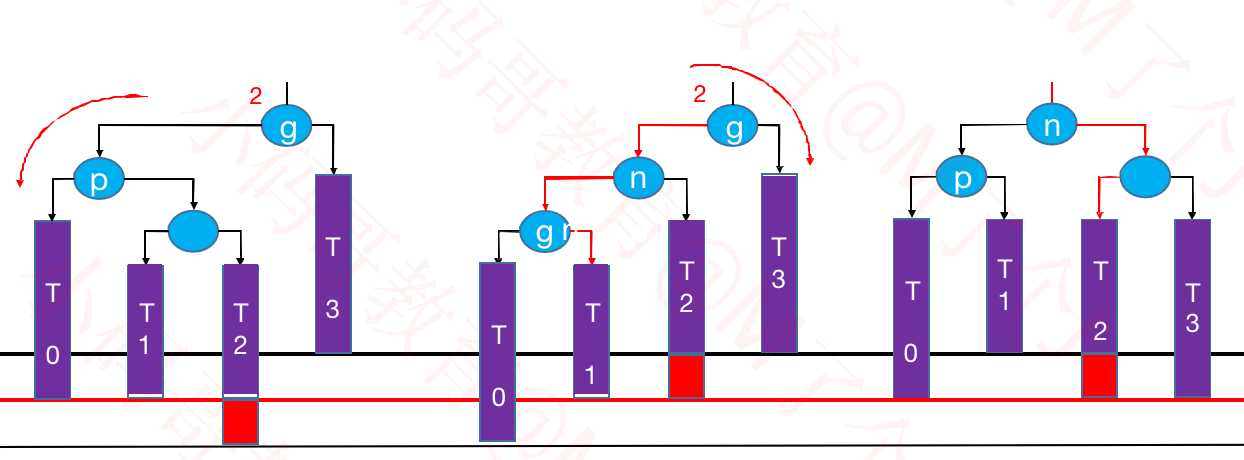
    ④RL – LL右旋转，RR左旋转（双旋）

     

    2.1.2 删除导致的失衡

    ? 示例：删除子树中的 16

    ? 可能会导致父节点或祖先节点失衡（只有1个节点会失衡），其他节点，都不可能失衡

   

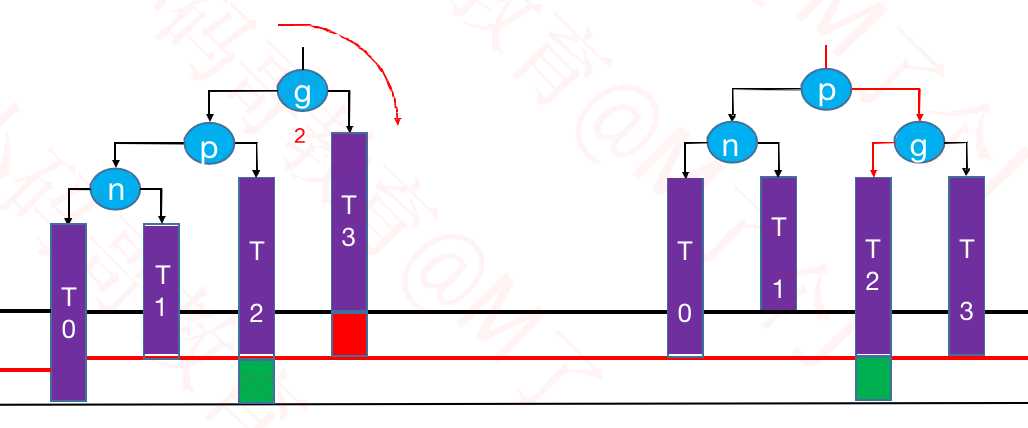
①LL – 右旋转（单旋）

? 如果绿色节点不存在，更高层的祖先节点可能也会失衡，需要再次恢复平衡，然后又可能导致更高层的祖先节点失衡...

? 极端情况下，所有祖先节点都需要进行恢复平衡的操作，共 O(logn) 次调整

② RR – 左旋转（单旋）

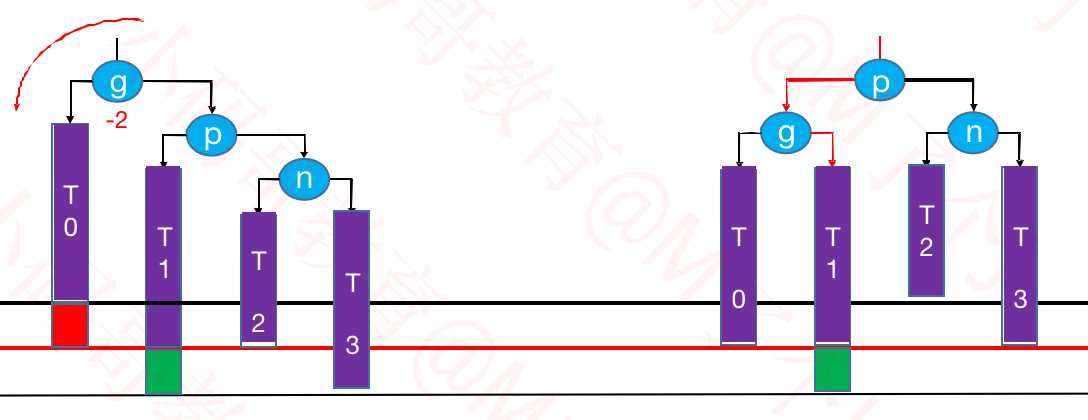
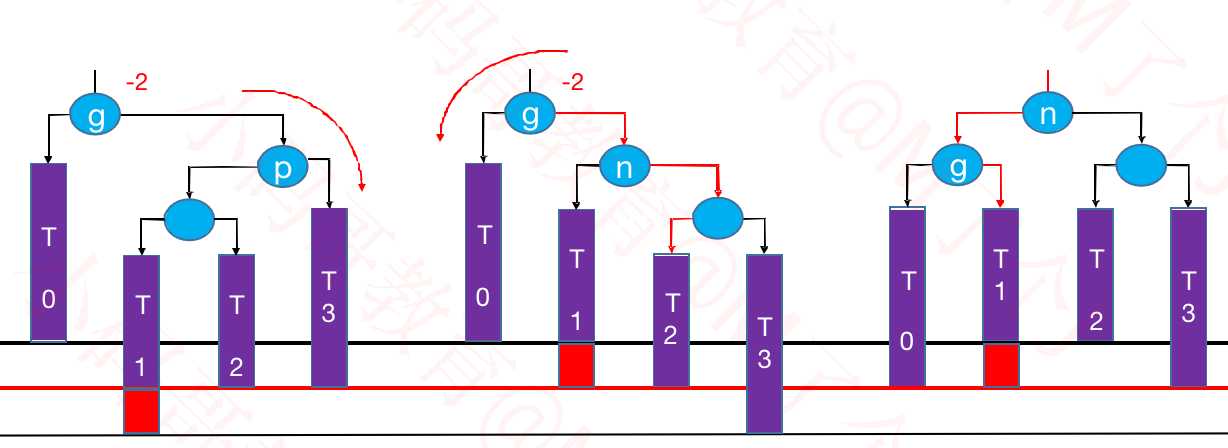
③LR – RR左旋转，LL右旋转（双旋）

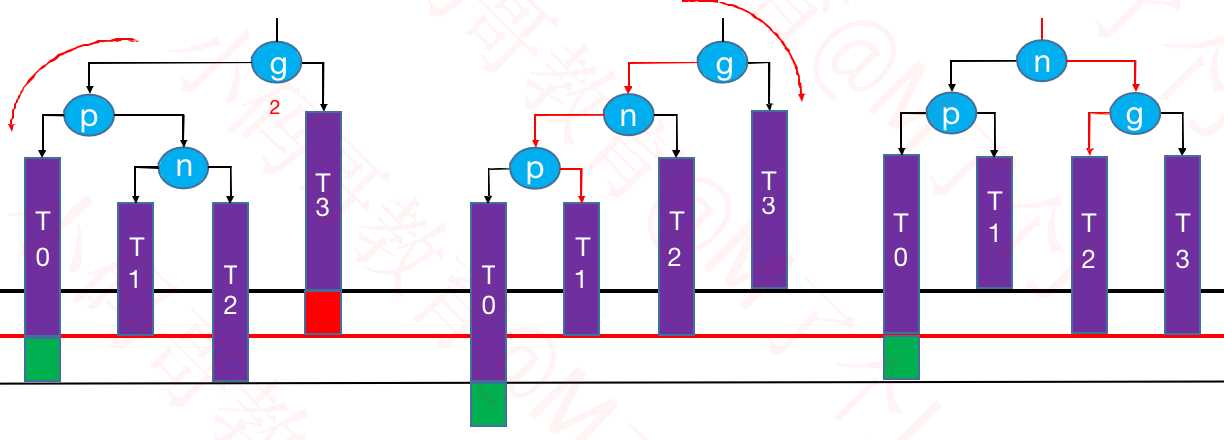
④RL – LL右旋转，RR左旋转（双旋）

 

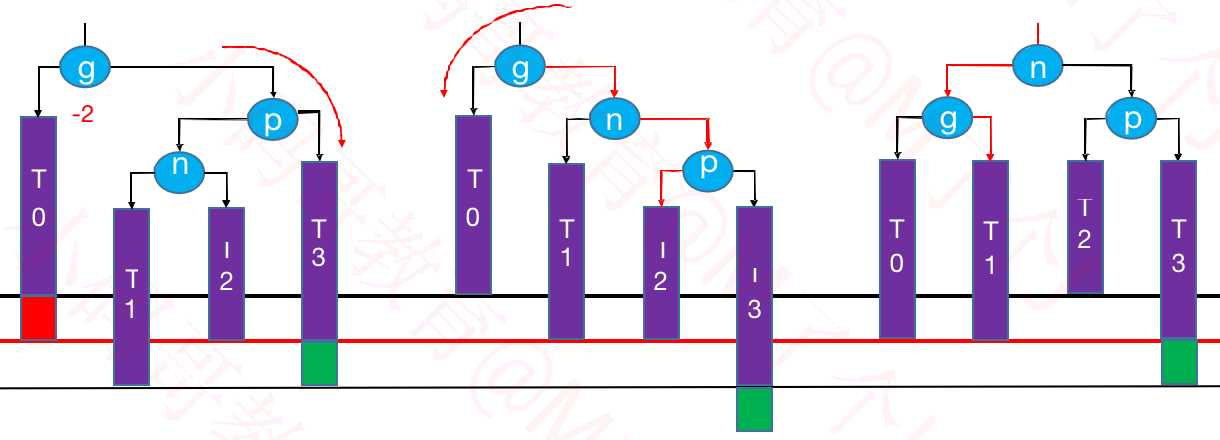
2.1.2 AVL树的总结：

① 添加

可能会导致所有祖先节点都失衡

只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡【仅需 O(1) 次调整】

② 删除

可能会导致父节点或祖先节点失衡（只有1个节点会失衡）

恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要 O(logn) 次调整】

平均时间复杂度

搜索：O(logn)

添加：O(logn)，仅需 O(1) 次的旋转操作

删除：O(logn)，最多需要 O(logn) 次的旋转操作

2.2 红黑树

 也叫做平衡二叉B树（Symmetric Binary

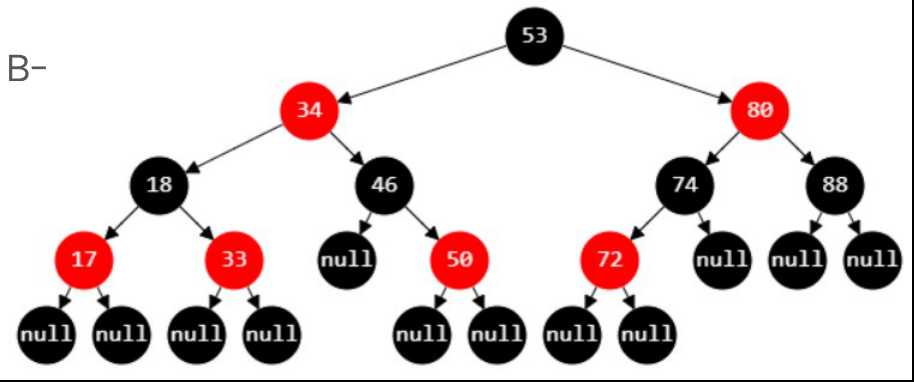
? 红黑树必须满足以下 5 条性质

1. 节点是 RED 或者 BLACK

2. 根节点是 BLACK

3. 叶子节点（外部节点，空节点）都是 BLACK

4. RED 节点的子节点都是 BLACK

  ① RED 节点的 parent 都是 BLACK

  ② 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点

5.从任一节点到叶子节点的所有路径都包含相同数目的BLACK 节点

2.2.1 红黑树和4阶B树（2-3-4树）具有等价性

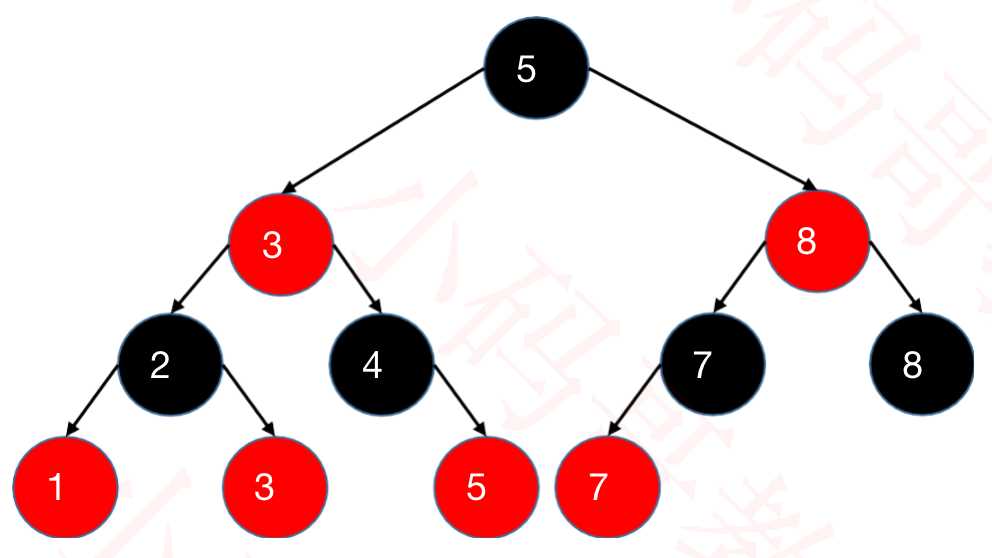
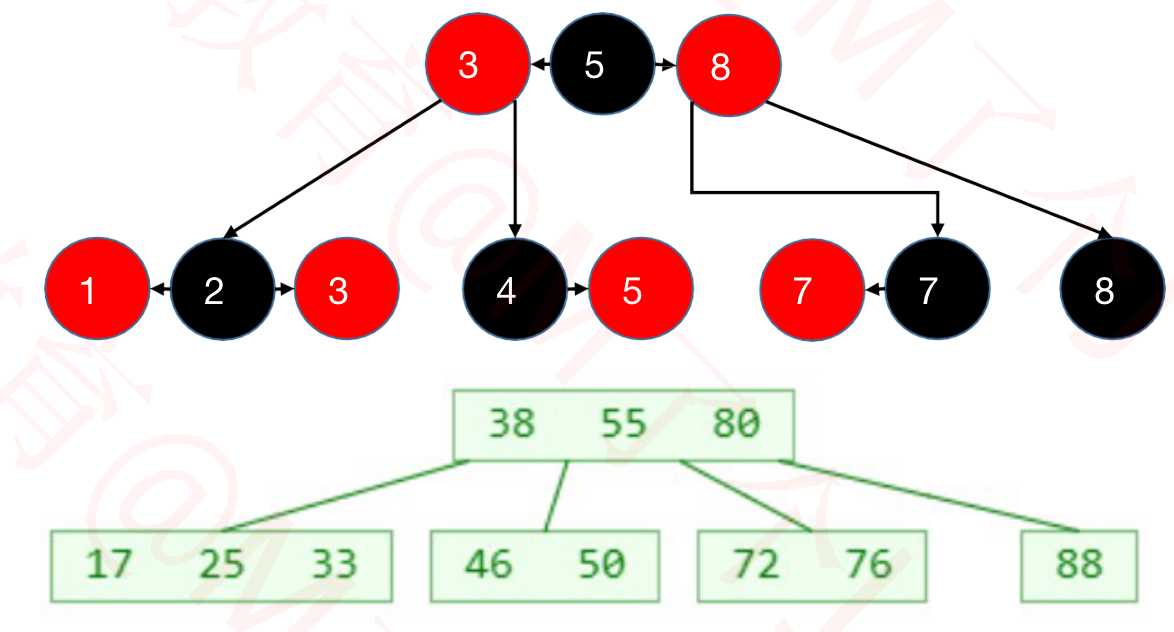
? BLACK 节点与它的 RED 子节点融合在一起，形成1个B树节点

? 红黑树的 BLACK 节点个数 与 4阶B树的节点总个数 相等

? 网上有些教程：用 2-3树 与 红黑树 进行类比，这是极其不严谨的，2-3树 并不能完美匹配 红黑树 的所有情况

? 注意：因为PPT界面空间有限，后面展示的红黑树都会省略 NULL 节点

2.2.2 添加导致的失衡

2.2.3 删除导致的失衡

2.2.4 红黑树性质总结

最初遗留的困惑：为何那5条性质，就能保证红黑树是平衡的？

p 那5条性质，可以保证 红黑树 等价于 4阶B树 

? 相比AVL树，红黑树的平衡标准比较宽松：没有一条路径会大于其他路径的2倍

? 是一种弱平衡、黑高度平衡

? 红黑树的最大高度是 2 ∗ log2(n + 1) ，依然是 O(logn) 级别

? 搜索：O(logn)

? 添加：O(logn)，O(1) 次的旋转操作

? 删除：O(logn)，O(1) 次的旋转操作