1111.有效括号的嵌套深度

Posted 2020-11-27 jiewl

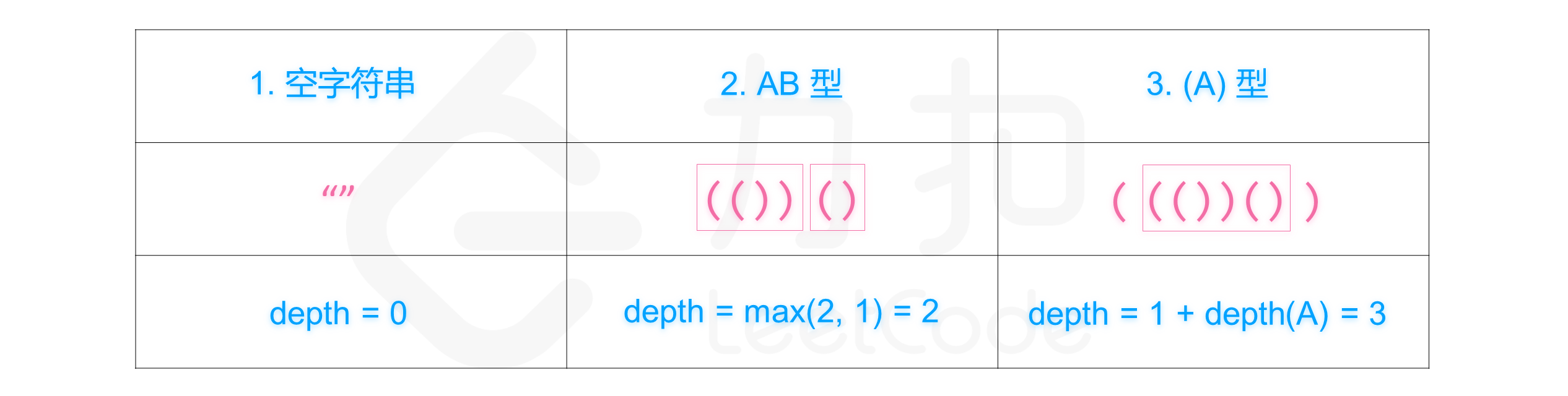
有效括号字符串 定义：对于每个左括号，都能找到与之对应的右括号，反之亦然。详情参见题末「有效括号字符串」部分。

嵌套深度 depth 定义：即有效括号字符串嵌套的层数，depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。

有效括号字符串类型与对应的嵌套深度计算方法如下图所示：

给你一个「有效括号字符串」 seq，请你将其分成两个不相交的有效括号字符串，A 和 B，并使这两个字符串的深度最小。

不相交：每个 seq[i] 只能分给 A 和 B 二者中的一个，不能既属于 A 也属于 B 。
A 或 B 中的元素在原字符串中可以不连续。
A.length + B.length = seq.length
深度最小：max(depth(A), depth(B)) 的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示，编码规则如下：

answer[i] = 0，seq[i] 分给 A 。
answer[i] = 1，seq[i] 分给 B 。
如果存在多个满足要求的答案，只需返回其中任意 一个 即可。

首先要解决的是括号如何划分，如果括号字符串深度只有1，那么可以全部划给A，如果深度有2，深度为1的字符串划给A，深度为2的划给B，那么A和B深度都为1，同理，深度为3时，深度为1和3的括号划给A，深度为2的划给B，那么A深度为2，B深度为1。所以可以把深度为奇数的分给A，为偶数的划给B。

class Solution {
    public int[] maxDepthAfterSplit(String seq) {
    	int[] res = new int[seq.length()];
    	char[] chars = seq.toCharArray();
    	int depth = 0;
    	for(int i = 0; i < chars.length; i ++) {
    		if(chars[i] == ‘(‘) {
    			depth++;
    			res[i] = depth%2;
    		}else {
                //为了保证右括号和左括号深度一样,应该先划分再深度减一
    			res[i] = depth%2;
    			depth--;
    		}
    	}
    	return res;
    }
}

还有一种思路，A和B首先深度都为0，当A深度小于B时，把左括号分给A，否则分给B，降低深度时（也就是分右括号）如果A深度高，就分给A，否则分给B

class Solution {
    public int[] maxDepthAfterSplit(String seq) {
    	int[] res = new int[seq.length()];
    	char[] chars = seq.toCharArray();
    	int a = 0;
    	int b = 0;
    	for(int i = 0; i < chars.length; i++) {
    		if(chars[i] == ‘(‘) {
    			if(a < b) {
    				a++;
    				res[i] = 0;
    			}else {
					b++;
					res[i] = 1;
				}
    		}else {
    			if(a >= b) {
    				a--;
    				res[i] = 0;
    			}else{
    				b--;
    				res[i] = 1;
    			}
    		}
    	}
    	return res;
    }
}