面试题60： n个骰子的点数替换空格（C++）

Posted 2020-11-27 wzw0625

题目地址：https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/

题目描述

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

题目示例

示例 1:

输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:

输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.1

解题思路

投掷n个骰子，所有点数出现的总次数是 6^n ，因为一共有n枚骰子，每枚骰子的点数都有6种可能出现的情况。

动态规划：我们用二维数组dp[i][j]表示投掷完i枚骰子后，点数j出现的次数（这里的点数指的是前n枚骰子的点数和，而不是第n枚骰子的点数），初始条件为dp[1][1]=dp[1][2]=dp[1][3]=dp[1][4]=dp[1][5]=dp[1][6]=1;状态转移方程为

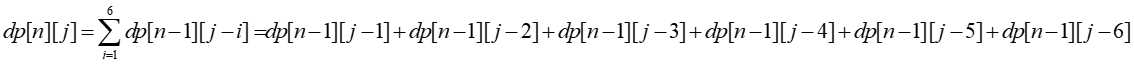
其中，n表示阶段，即投掷完了多少枚骰子，j表示投掷完n枚骰子后，可能出现的点数和，i表示第n枚骰子会出现的六个点数。

动态规划的空间优化：因为每个阶段的状态都只和它前一阶段的状态有关，因此我们不需要用额外的一维来保存所有阶段。我们可以用一维数组来保存一个阶段的状态，然后对下一个阶段可能出现的点数j从大到小遍历，实现一个阶段到下一阶段的转换。

程序源码

动态规划

class Solution {
public:
    vector<double> twoSum(int n) {
        vector<vector<int>> dp(n + 1, vector<int>(6 * n + 1, 0));
        //初始化
        for(int i = 1; i <= 6; i++)
        {
            dp[1][i] = 1;
        }
        //计算dp
        for(int i = 2; i <= n; i++) //从2到n计算dp
        {
            for(int j = i; j <= 6 * i; j++) //当n=i时的点数和
            {
                for(int k = 1; k <= 6; k++) //状态转移方程计算
                {
                    dp[i][j] += dp[i - 1][j - k];
                    if(j - k <= 0) break; //若第i个骰子的点数比第i-1个的点数小，错误处理
                }
            }
        }
        int all_counts = pow(6, n);
        vector<double> res;
        //计算投掷完n枚骰子后，点数j出现的次数与总的次数的比值，即(所有骰子出现的次数/总的次数)
        for(int j = n; j <= 6 * n; j++)
        {
            res.push_back(dp[n][jj * 1.0 / all_counts);
        }
        return res;
    }
};

动态规划—空间优化

class Solution {
public:
    vector<double> twoSum(int n) {
        vector<int> dp(6 * n + 1, 0);
        //初始化
        for(int i = 1; i <= 6; i++)
        {
            dp[i] = 1;
        }
        //计算dp
        for(int i = 2; i <= n; i++) //从2到n计算dp
        {
            for(int j = 6 * i; j >= i; j--) //当n=i时的点数和
            {
                dp[j] = 0;
                for(int k = 1; k <= 6; k++) //状态转移方程计算
                {
                    dp[j] += dp[j - k];
                    if(j - k <= i - 1) break; //若第i个骰子的点数比第i-1个的点数小，错误处理
                }
            }
        }
        int all_counts = pow(6, n);
        vector<double> res;
        //计算投掷完n枚骰子后，点数j出现的次数与总的次数的比值，即(所有骰子出现的次数/总的次数)
        for(int j = n; j <= 6 * n; j++)
        {
            res.push_back(dp[j] * 1.0 / all_counts);
        }
        return res;
    }
};

参考文章

动态规划初级试炼场：https://mp.weixin.qq.com/s/Ef73zZv6wiaXwiJRnCLpoQ