"美团杯"热身题(数独)

Posted 2020-11-27 hznudreamer

虽然之前没做过数独，不知道这种题是咋出出来的，但的确每一步都能通过一定的推理确定，不含赌的成分(话说假设法不算赌吧quq)。

每一行每一列每一个九宫格内1-9只出现一次，从带有圆球一端开始每条曲线上的数字严格递增。

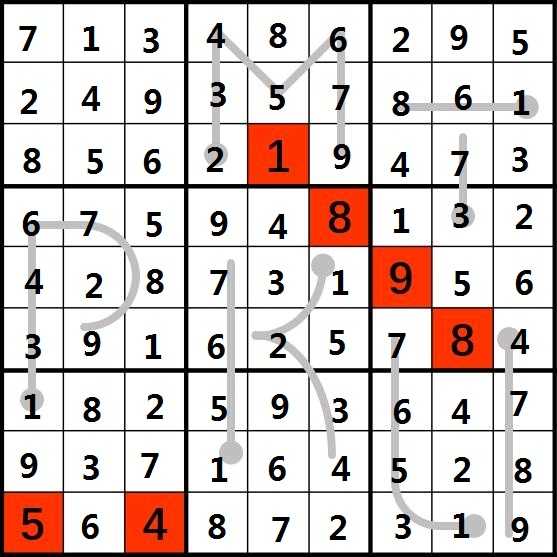
先给原图：

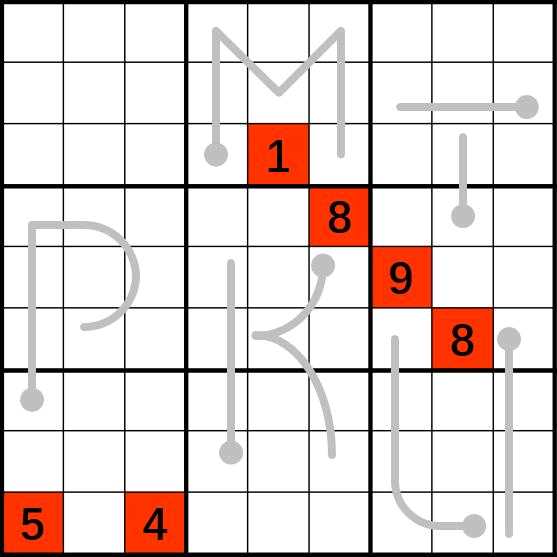
以下提供一种解题思路：

1.考虑字母M，因为(4,6)含有数字8，因此字母M第6列的位置不含8，而M中的数字严格递增，可以推得，在M的九宫格中，8必然位于(1,5)处，此时该九宫格已经确定2个数字，其余的数字严格递增，因此也能够确定，那么这个九宫格的数字就已经完全确定了。

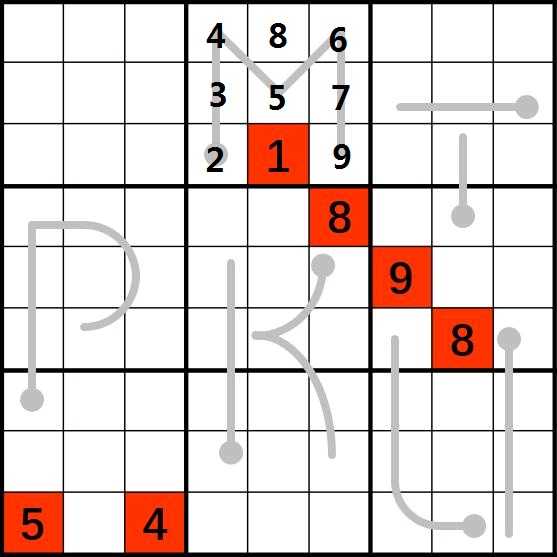
2.考虑字母K，K的第4列自下向上严格递增，而因为(4,6)含有数字8，因此该九宫格内不再含8，又因为K的第4列严格递增，8不可能位于(4,7)和(4,8)，如此一来，8只能位于(4,9)。又由于严格递增和(5,7)处含有数字9,所以第4列的9只能位于(4,4)。此时第4列除了K的边上的元素都已经确定，根据严格递增，这条边上的元素也能够确定，这样就把第4列完全确定了。

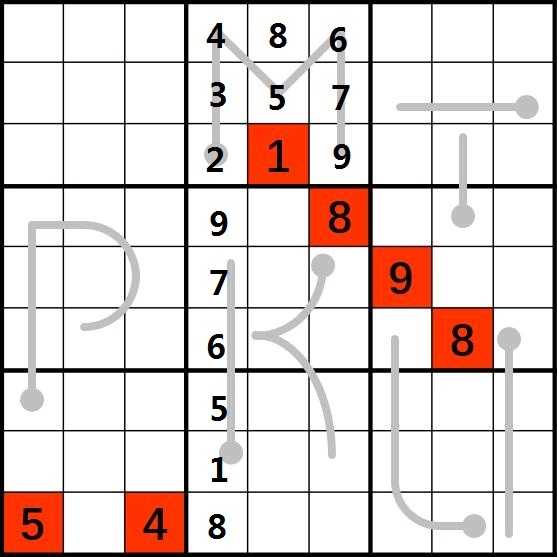
3.考虑(7,4)和(2,5)含有数字5，因此第6列的5必然位于(5,6)或者(6,6)，又考虑(4,6)含数字8，假设5位于(5,6)，由于K上数字严格递增，则必然会在(7,6)或者(8,6)出现数字8，但该列本身已经含有数字8，因此5位于(5,6)是不成立的，所以第6列的5只能位于(6,6)。

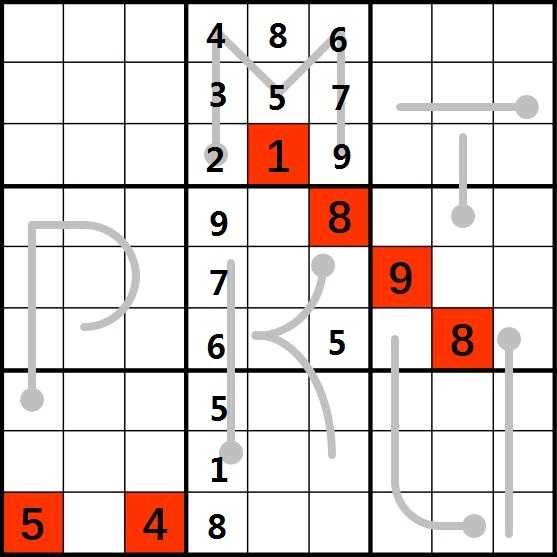
4.此时第6列还有1,2,3,4没有填入。考虑K的严格递增，3和4只能位于(7,6)和(8,6)，1只能位于(5,6)，这样一来剩下的2只能位于(9,6)，同时可以确定(6,5)处应填2。

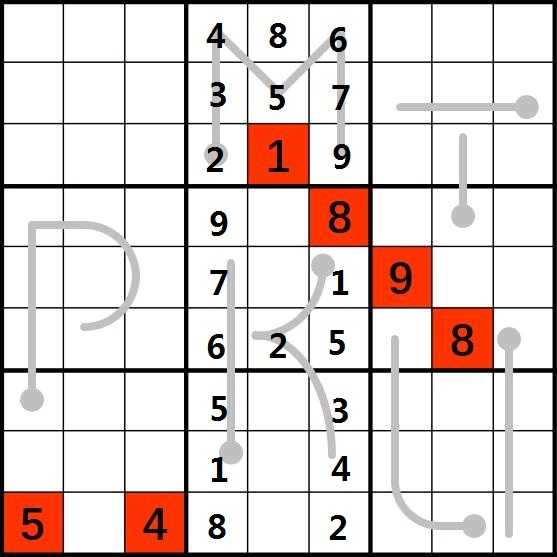
5.考虑(6,7)，根据之前所填的数可以确定，该位置不能为5、6、8、9，而该位置位于字母L的最后一个位置，也就是第5个位置，所以它至少是第5大的数，所以它必然>=5，结合之前的判断，该位置只能为7。

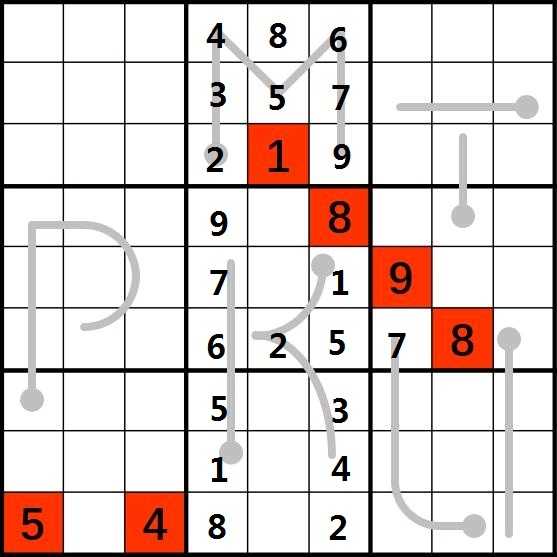
6.考虑(7,7)，由于它在数字7以下，所以该位置<=6，由于(7,4)含数字5，该位置不能为5，又由于该位置在L严格递增的第4位，因此它>=4，所以可以判断它只能为4或者6，假设它为4，那么根据严格递增，(9,7)必为2，但(9,6)已经确定为2，因此(7,7)只能为6。此时考虑(7,6)，它在6之下，所以它应<=5，又它在L严格递增第三位，它应>=3，又(8,6)已经确定为4，所以该位置必为5。考虑(9,7)和(9,8)，由于(9,3)为数字4，(9,6)为数字2，因此(9,7)只能为3，(9,8)只能为1。至此字母L完全确定。

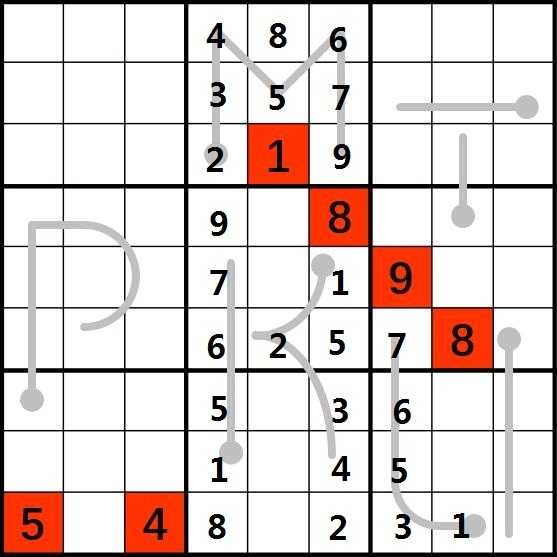
7.考虑字母P。由于(4,4)和(5,7)为数字9以及考虑P的严格递增，因此第6行的9必然位于(6,2)或者(6,3)，假设位于(6,3)，由于(6,7)为7以及(6,8)为8，所以(6,2)<=6，但(6,2)位于P严格递增的第7位，该位置必然>=7，因此矛盾，所以第6行的9必然位于(6,2)。同理，考虑第5行的数字8，由于(4,6)和(6,8)为数字8以及P严格递增，所以第5行的8必然位于(5,2)或者(5,3)，假设位于(5,2)，由于(5,4)为7，所以(5,3)<=6，又由于它位于P递增的第6位，所以它又>=6，所以它=6，依次反推可得(6,1)为2，但(6,5)已经为2，所以该方案错误，所以第5行的8应该位于(5,3)。同理考虑第4行的7，由于(5,4)和(6,7)为7和P的递增，第4行的7只能位于(4,2)或者(4,3)，假设位于(4,3)，依据P的递增性和利用(9,1)的5和(6,5)的2可以用类似之前的排除法排除掉这种情况，第4行的7应该位于(4,2)。

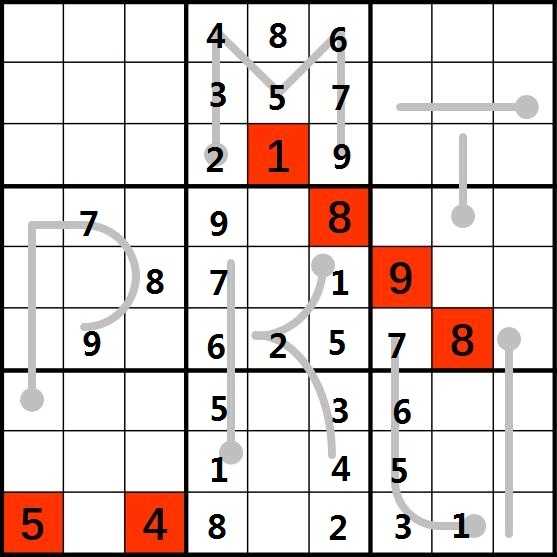
8.考虑第一列。(9,1)为5，考虑(4,1)应该<=6并且>=4并且!=5，考虑如果=4，(6,1)必为2，而(6,5)已经为2，所以不符合，所以(4,1)必为6。考虑(5,1)应该<=5并且>=3并且!=5，考虑如果为3，那(6,1)为2，和之前一样是不符合的，所以(5,1)必为4。同理(6,1)<=3并且>=2，又(6,5)为2，所以(6,1)!=2，所以(6,1)必为3。

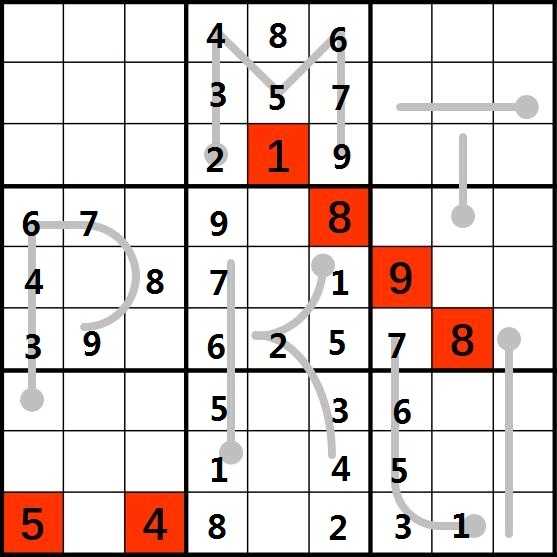
9.考虑最后一行。剩下3个数6,7,9。考虑(9,2)，由于(4,2)为7，(6,2)为9，所以(9,2)必为6。考虑中间的九宫格，还剩3,4没填，由于(5,1)已经为4，所以(4,5)为4，(5,5)为3。

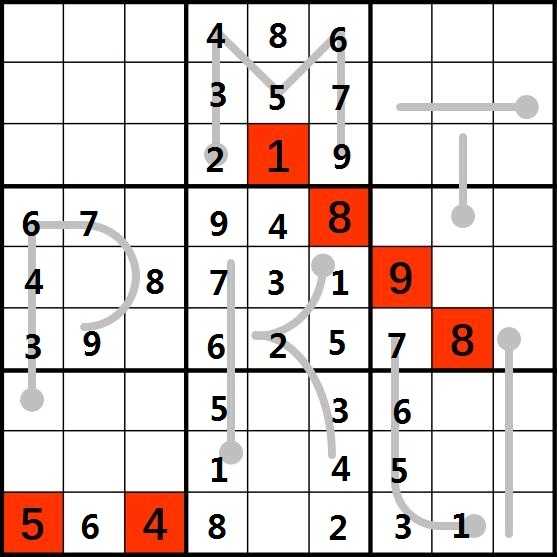
10.根据每行每列元素要不同把(6,3)的1、(6,9)的4、(8,5)的6补上。

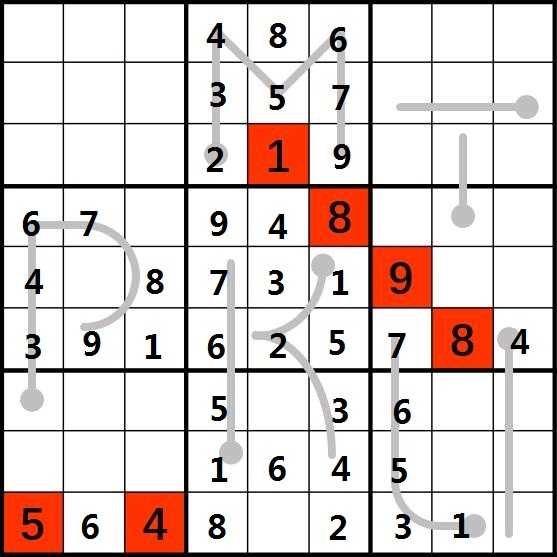
11.考虑字母I。由I的递增性，(7.9) >= 5，(7,4)为5，(7,7)为6，因此(7,9) >= 7，由于(7,9)之后还有2位，所以只能是(7,9)为7，(8,9)为8，(9,9)为9。填完之后补上(9,5)的7和(7,5)的9还有(7,8)的4和(8,8)的2。

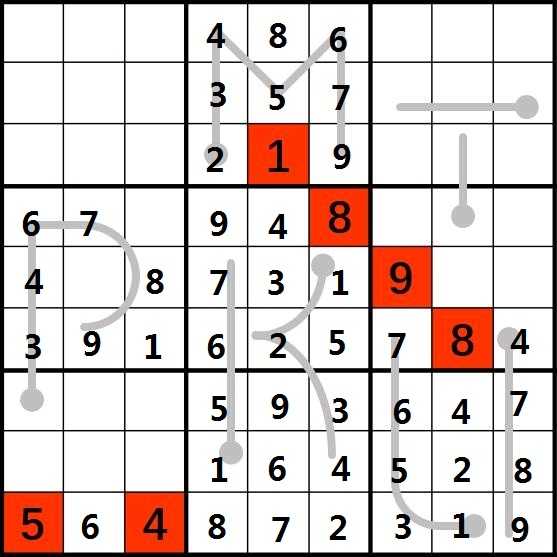
12.考虑第7行的8。由于(5,3)和(8,9)的8已经确定，又(7,1)只能是1或者2，因此第7行的8只能位于(7,2)。然后考虑(7,1)，由于(6,3)为1，所以(7,1)为1，所以(7,3)为2。根据九宫格内元素不同和同一行同一列元素不同把(4,3)的5和(5,2)的2补上。

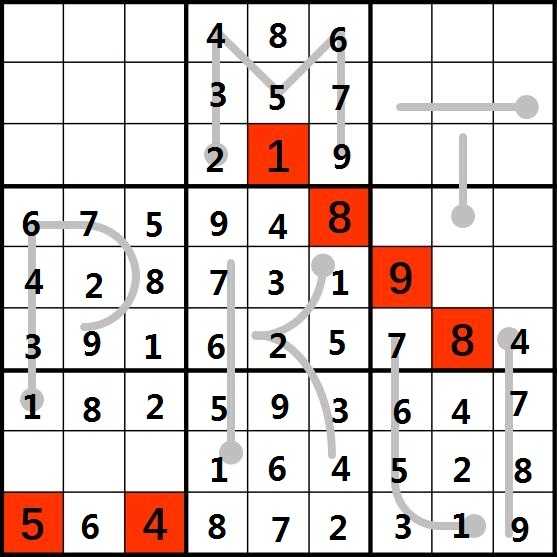
13.根据(5,7)和(9,9)的9以及字母T的递增性补上(1,8)的9。考虑第4行，剩下1,2,3没填，考虑第8列有1,2，所以(4,8)为3。

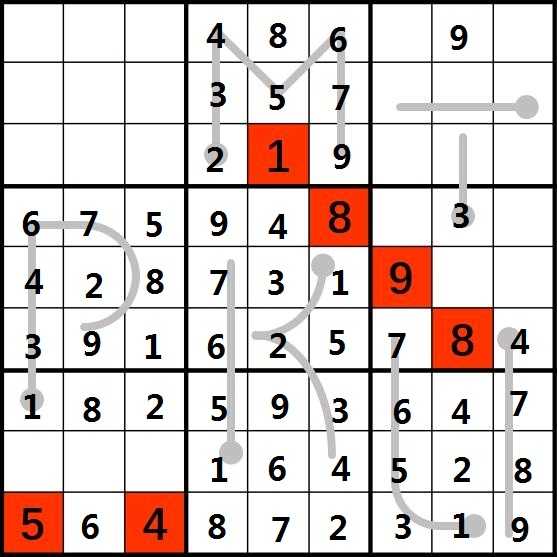
14.考虑第7列的4，由于(1,4)和(4,5)以及确定有4，所以第7列的4只能在(2,7)或者(3,7)，假设在(2,7)，由于第8列已经确定含有1,2,3，因此由字母T的递增性确定不可能在(2,7)，所以第7列的4在(3,7)。继续考虑第7列的8，由于(1,5)和(4,6)已经确定含8，因此第7列的8位于(2,7)。

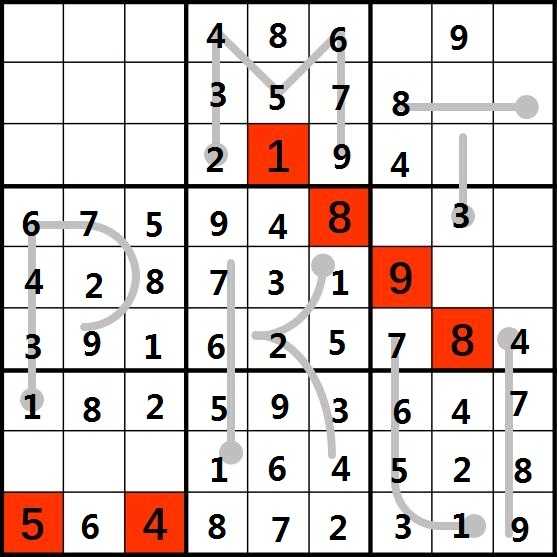
15.由(5,1)、(9,3)、(1,4)、(3,7)的4可以确定第一个九宫格内的4位于(2,2)。

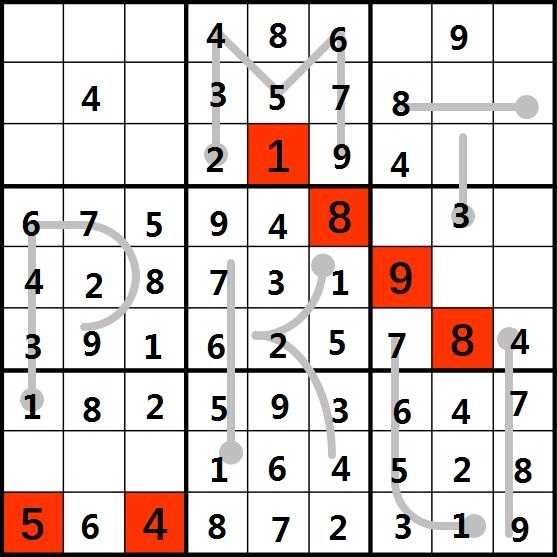
16.至此，大部分元素已经确定，剩下部分已经不成问题，只需按照题目要求拼拼凑凑(或者说乱搞?)就能得到最终答案。