Decision tree——决策树

Posted 2020-11-27 qizhou

基本流程

　　决策树是通过分次判断样本属性来进行划分样本类别的机器学习模型。每个树的结点选择一个最优属性来进行样本的分流，最终将样本类别划分出来。  

　　决策树的关键就是分流时最优属性$a$的选择。使用所谓信息增益$Gain(D,a)$来判别不同属性的划分性能，即划分前样本类别的信息熵，减去划分后样本类别的平均信息熵，显然信息增益越大越好：

$ ext{Ent}(D)=-sumlimits_{k=1}^{|mathcal{Y}|}p_klog_{2}p_k$
$displaystyle ext{Gain}(D,a)= ext{Ent}(D)-sumlimits_{v=1}^{V}frac{|D^v|}{|D|} ext{Ent}(D^v)$

　　其中$D$是划分前的数据集，$|mathcal{Y}|$是样本的类别数，$p_k$是数据集中类别$k$的比例，$D^v$是划分后的某个数据集，$V$是数据集的分流数量。

　　又考虑到可能有的属性取值过多，直接将样本划分为多个只包含一个样本的集合，信息熵变为了0。如此似乎取得最大的信息增益，但实际上是过拟合了。因此，还要使用“增益率”来平衡，除了信息增益要大外，划分出的集合数要小。增益率定义如下：

$ ext{Gain_ratio}(D,a)=displaystyle frac{ ext{Gain(D,a)}}{ ext{IV}(a)},$

$displaystyle ext{IV}(a)=-sumlimits_{v=1}^Vfrac{|D^v|}{|D|}log_{2}frac{|D^v|}{|D|}$

　　另外，也不能一味地取增益率大的属性，因为大增益率偏好属性种类少的属性，也就会偏好连续属性（因为连续属性是取一个划分点来将样本划分为两部分，而离散属性则可能有多个属性种类）。因此通常会启发性地先选出信息增益大于平均值的属性，再从其中选择增益率最大的属性。

实验

　　训练数据集使用西瓜数据集：

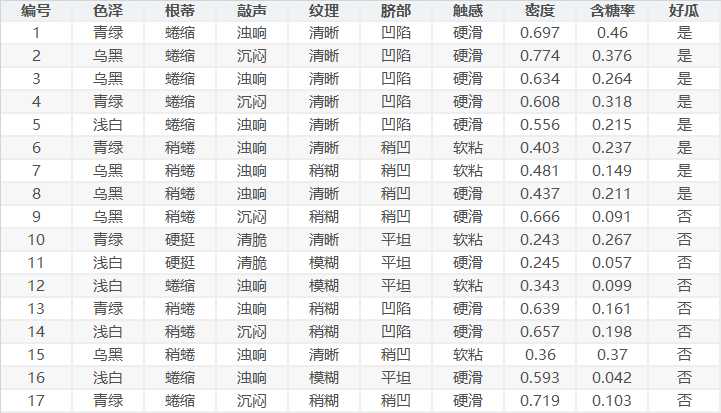
　　实验没有使用python的机器学习包sklearn，分别测试了使用与不使用增益率来生成决策树。 首先自定义树结点的结构，分别是离散属性结点、连续属性结点与叶结点，如下：

 1 node(离散):
 2 { 
 3     "divide_attr": ["纹理", 3, 0, 0],        //0：属性名称（第几个属性） //1：属性序号  //2：0离散，1连续     //3：连续属性的划分点
 4     "if_leave": false,            //是否为叶结点 
 5     "info_gain": 0.3805918973682686,    //信息增益
 6     "gain_ratio": 0.2630853587192754,    //信息率
 7     "divide": 
 8     {
 9         "清晰":node,
10         "稍糊":node,
11         "模糊":node
12     }//存各个样式的结点
13 }
14 node(连续):
15 { 
16     "divide_attr": ["密度", 6, 1, 0.3815],        
17     "if_leave": false,            
18     "info_gain": 0.7642045065086203,    
19     "gain_ratio": 1.0,    
20     "divide": 
21     {
22         "0":node,            //小于等于划分点
23         "1":node            //大于划分点
24     }//存各个样式的结点 
25 }
26 node(叶结点):
27 {
28     "if_leave":true,
29     "class":"是"            //判断类别
30     "samples":[...]            //存生成决策树时划分到这个叶结点的样本
31 }

　　结点使用字典存储。

　　将数据输入Excel中并在python中读入，然后使用处理好的数据生成决策树。以下是不使用增益率生成的决策树结构：

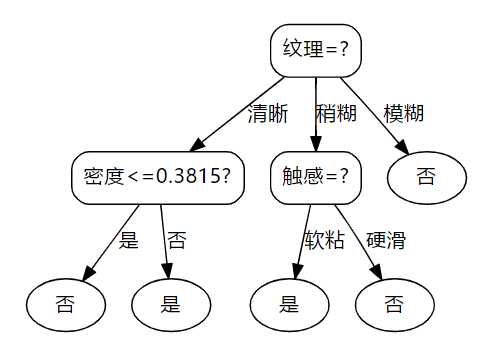
　　以下是使用增益率生成的决策树结构：

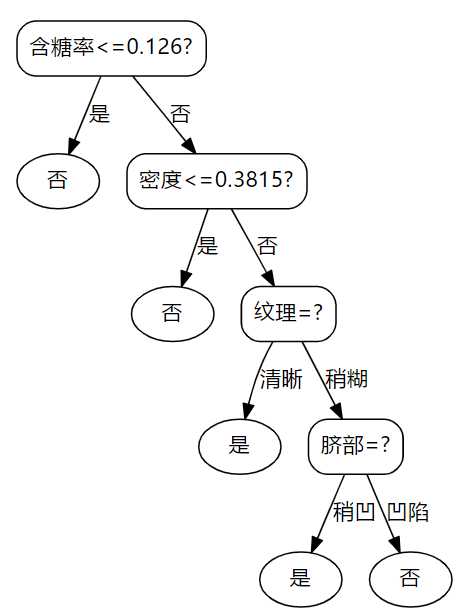
　　对比可以发现，当增益率参与决策树的生成时，连续属性会优先被使用。使用以上二者进行对训练集进行测试的正确率都是1.0。以下是处理数据、生成决策树、训练集验证、画出决策树结构的代码：

  1 #%%
  2 import matplotlib as plt
  3 import numpy as np
  4 import xlrd
  5 import sys
  6 
  7 table = xlrd.open_workbook(‘data.xlsx‘).sheets()[0]#读取Excel数据
  8 data = []
  9 for i in range(0,table.nrows):
 10     data.append(table.row_values(i))  
 11  
 12 attr_type = np.zeros([len(data[0])-2])#获取属性类型0离散，1连续
 13 for i in range(len(attr_type)):
 14     if type(data[1][i+1]) == str:
 15         attr_type[i] = 0
 16     else:
 17         attr_type[i]=1
 18 
 19 data = np.array(data)[:,1:] #转为数字矩阵 并去掉序号
 20 all_attr = data[0,:-1]  #存属性名称
 21 data = data[1:]#去掉表头   
 22    
 23 #%%
 24 def get_info_entropy(a):
 25     """
 26     传入array或list计算类别的信息熵
 27     """
 28     c = {}
 29     n = len(a)
 30     for i in a:
 31         if i not in c.keys(): 
 32             c[i] = 1
 33         else:
 34             c[i] += 1
 35     entropy = 0
 36     for i in c.keys():
 37         p = c[i]/n
 38         entropy += -p*np.log2(p) 
 39     return entropy  
 40 
 41 def info_gain_and_ratio(D,s):
 42     """
 43     传入原数据集、按属性分类后的字典s
 44     """
 45     info_gain  = get_info_entropy(D[:,-1])
 46     class_entro = 0 
 47     for i in s.keys():
 48         n = len(s[i])
 49         info_gain -= n/len(D)*get_info_entropy(s[i][:,-1])
 50         class_entro-=n/len(D)*np.log2(n/len(D))
 51     if class_entro == 0:
 52         return info_gain,info_gain
 53     return info_gain,info_gain/class_entro
 54     
 55 
 56 def attr_classfier(D,an,if_dic): 
 57     """ 
 58     传入：数据集、分类属性序号、是否传出字典
 59     使用属性对D进行分类
 60     传出：
 61     1、离散：以属性值为key，以分类后的数据集为value的字典dictionary 
 62     连续：key为0时<bound，为1时>bound
 63     2、连续属性的最优分界点float，离散的传出0
 64     3、类别信息增益
 65     4、增益率
 66     """
 67     dic = {}
 68     opt_bound = 0
 69     info_gain = 0
 70     gain_ratio = 0
 71     if attr_type[an] == 0:#离散属性获得分类数据集
 72         for i in D:
 73             if i[an] not in dic.keys():
 74                 dic[i[an]] = [i]
 75             else:
 76                 dic[i[an]].append(i)
 77         for i in dic.keys():
 78             dic[i] = np.array(dic[i]) 
 79         info_gain,gain_ratio = info_gain_and_ratio(D,dic)
 80     elif attr_type[an] == 1:#连续属性获得分类数据集
 81         attrs = D[:,an]
 82         attrs = np.sort(attrs.astype(float))
 83         for i in range(len(attrs)-1): 
 84             bound = (attrs[i]+attrs[i+1])/2
 85             dic0 = {} #每次都初始化
 86             dic0[‘0‘] = []
 87             dic0[‘1‘] = [] 
 88             for j in D:
 89                 if float(j[an]) <= bound:
 90                     dic0[‘0‘].append(j)
 91                 else:
 92                     dic0[‘1‘].append(j) 
 93             for j in dic0.keys():
 94                 dic0[j] = np.array(dic0[j])
 95             t,b = info_gain_and_ratio(D,dic0) 
 96             if t>info_gain:
 97                 dic = dic0
 98                 opt_bound = bound
 99                 info_gain = t
100                 gain_ratio = b
101     if if_dic:
102         return dic,opt_bound,info_gain,gain_ratio
103     return opt_bound,info_gain,gain_ratio  
104 
105 def get_most_class(d):
106     """
107     获取数据集中占比最大的类别
108     """
109     c = {}  
110     for i in d[:,-1]:
111         if i not in c.keys(): 
112             c[i] = 1
113         else:
114             c[i] += 1
115     m = ""
116     for i in c.keys():
117         if m == "":
118             m = i
119         elif c[i] > c[m]:
120             m = i
121     return m
122             
123 #%%
124 def get_opt_attr(ave_info_gain,info_gains,gain_ratios,A,use_gain_ratios):
125     """
126     获取最优属性传入：
127     1、平均信息增益
128     2、所有属性的信息增益
129     3、所有属性的信息率
130     4、属性可用list
131     5、是否使用信息率
132     """
133     opt_attr_index = 0
134     #获取最优属性 
135     for i in range(len(A)):
136         if A[i] == 1:
137             if info_gains[i] > ave_info_gain:#在信息增益大于平均中取最大信息率
138                 if use_gain_ratios:
139                     if gain_ratios[i] > gain_ratios[opt_attr_index]:
140                         opt_attr_index = i ################取到最优属性了 
141                 else:
142                     if info_gains[i] > info_gains[opt_attr_index]:
143                         opt_attr_index = i
144     return opt_attr_index
145 
146 def create_node(D,A,use_gain_ratios):
147     ‘‘‘
148     :传入数据集和属性集
149     :D传入数据集的切片
150     :A传入属性的使用矩阵，如[1,1,1,0,0,0,1],1表示可使用，0表示已使用
151     :函数同一类别的先判断，之后属性取值全相同和划分属性放一起
152     ‘‘‘
153     node = {}
154     if len(set(D[:,-1])) == 1:#类别全相等，叶结点
155         node["if_leave"]=True
156         node["class"]=D[0,-1]
157         node["samples"] = D.tolist()
158         return node 
159     info_gains = np.zeros([len(A)]) #所有可用属性得出的信息增益
160     ave_info_gain = 0#平均信息增益
161     gain_ratios = np.zeros([len(A)])#所有可用属性得出的信息增益率
162     opt_attr_index = 0#大于平均信息增益的属性中，增益率最大的属性索引
163     attr_bound = np.zeros([len(A)])   #连续属性的属性界限
164     active_attrN = 0 #可用属性数，用于求信息增益平均 
165     for i in range(len(A)):
166         if A[i] == 1:
167             attr_bound[i],info_gains[i],gain_ratios[i] =  attr_classfier(D,i,False)
168             ave_info_gain += info_gains[i]
169             active_attrN += 1 
170     """
171     以下判断之一成立，即为叶结点，没有分下去的意义：
172     # 1、所有属性增益率都太低  
173     # 2、所有属性是否分别在所有样本上取值都相同（同上，信息增益=0）  
174     # 3、可用属性为空
175     """
176     if ave_info_gain < 0.01 or active_attrN == 0:
177         node["if_leave"] = True
178         node["class"] = get_most_class(D[:,-1])#类别为数据集中最多的类
179         node["samples"] = D.tolist()
180         return node
181     #获取最优属性
182     opt_attr_index = get_opt_attr(opt_attr_index,info_gains,gain_ratios,A,use_gain_ratios) 
183     """
184     以下由最优属性生成子结点
185     """
186     dic,bound,info_gain,gain_ratio= attr_classfier(D,opt_attr_index,True)
187     if attr_type[opt_attr_index] == 0:#离散
188         A[opt_attr_index] = 0
189         node["divide_attr"] = [all_attr[opt_attr_index],opt_attr_index,0,0] 
190     elif attr_type[opt_attr_index] == 1:#连续
191         node["divide_attr"] = [all_attr[opt_attr_index],opt_attr_index,1,bound]
192     sons = {}
193     for i in dic.keys():
194         sons[i] = create_node(dic[i],A[:],use_gain_ratios) 
195     node["if_leave"] = False
196     node["info_gain"] = info_gain
197     node["gain_ratio"] = gain_ratio    
198     node["divide"] = sons
199     return node
200 
201 """
202 此处生成决策树，True使用增益率，False不用
203 """
204 root = create_node(data,np.ones([len(all_attr)]),False)
205 
206 #%%
207 """
208 以上训练好模型root，下面测试
209 """
210 def test_decision_tree(sample,tree):
211     decision = ""
212     while True:
213         if tree["if_leave"] == True:
214             decision = tree["class"]
215             break
216         if tree["divide_attr"][2] == 0:#离散
217             attr = tree["divide_attr"][1] 
218             tree = tree["divide"][sample[attr]]
219         elif tree["divide_attr"][2] == 1:#连续
220             attr = tree["divide_attr"][1] 
221             b = tree["divide_attr"][3]
222             if float(sample[attr]) <= b:
223                 tree = tree["divide"]["0"]
224             else:
225                 tree = tree["divide"]["1"]
226     return decision 
227 right = 0
228 for i in data: 
229     a = test_decision_tree(i,root) 
230     if i[-1] == a:
231         right +=1
232 print("正确率：" + str(right/len(data))) 
233 #%%
234 """
235 Json导出树的结构
236 """
237 import json
238 with open(‘decision tree.json‘,‘w‘,encoding=‘utf-8‘) as f:
239     f.write(json.dumps(root,ensure_ascii = False))
240 #%%
241 """
242 画出决策树结构
243 """ 
244 import pydotplus as pdp 
245 
246 def iterate_tree(tree,num): 
247     """
248     迭代决策树，递归出结点间的箭头map
249     """
250     map_str = ""
251     itenum = num 
252     if tree["if_leave"]:
253         map_str = str(num)+‘[label="‘ + tree["class"] + ‘"];‘ #类别
254         map_str += str(num)+‘[shape=ellipse];‘ #显示为椭圆
255     else: 
256         if tree["divide_attr"][2] == 0:#离散属性
257             map_str = str(num)+‘[label="‘ + tree["divide_attr"][0] + ‘=?"];‘ #判别属性
258             for i in tree["divide"].keys():
259                 itenum+=1
260                 map_str += str(num)+"->"+str(itenum)+‘[label="‘+ i +‘"];‘ #添加边与边标签
261                 son_map_str, itenum= iterate_tree(tree["divide"][i],itenum)
262                 map_str+=son_map_str
263         elif tree["divide_attr"][2] == 1:#连续属性 
264             map_str = str(num)+‘[label="‘ + tree["divide_attr"][0] +"<="+ str(tree["divide_attr"][3]) + ‘?"];‘ #判别属性标签
265             itenum+=1
266             map_str += str(num)+"->"+str(itenum)+‘[label="是"];‘ #添加边与边标签
267             son_map_str, itenum= iterate_tree(tree["divide"]["0"],itenum)
268             map_str+=son_map_str
269             itenum+=1
270             map_str += str(num)+"->"+str(itenum)+‘[label="否"];‘ #添加边与边标签
271             son_map_str, itenum= iterate_tree(tree["divide"]["1"],itenum)
272             map_str+=son_map_str
273 
274     return map_str,itenum
275 def get_decision_tree_map(tree):
276     map_str = """
277     digraph decision{
278         node [shape=box, style="rounded", color="black", fontname="Microsoft YaHei"]; 
279         edge [fontname="Microsoft YaHei"];   
280     """
281     mm,n = iterate_tree(tree,0) 
282     return map_str + mm + "}"  
283 
284 decision_tree_map =  get_decision_tree_map(root)
285 print(decision_tree_map)
286 graph = pdp.graph_from_dot_data(decision_tree_map)
287 graph.write_pdf("Decision tree.pdf")