降维实践（PCA，LDA）

Posted 2020-11-27 knight66666

17 降维简介

当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。
PCA、LDA降维一般假设数据集为线性可分，如果用这两种方法，对线性不可分的数据集进行降维，效果往往不理想。本质上PCA和LDA还是一种线性变换。而线性不可分数据应该是很普遍的，对线性不可分数据集该如何进行降维呢？这里我们介绍一种核PCA方法，这样降维方法综合了核技巧及PCA思想，对非线性数据集降维有非常好的效果。
此外，这里我们还介绍SVD方法，这也是一种非常有效的降维方法。

17.1 PCA简介

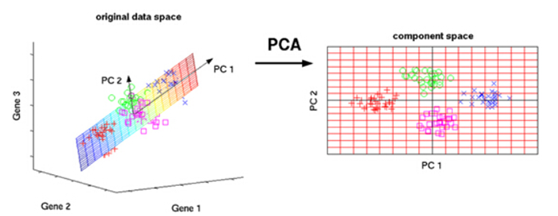
主成分分析（Principal Components Analysis），简称PCA，是一种数据降维技术，用于数据预处理。一般我们获取的原始数据维度都很高，比如1000个特征，在这1000个特征中可能包含了很多无用的信息或者噪声，真正有用的特征才50个或更少，那么我们可以运用PCA算法将1000个特征降到50个特征。这样不仅可以去除无用的噪声，还能减少很大的计算量。
PCA算法是如何实现的？
简单来说，就是将数据从原特征空间转换到新的特征空间中，例如原始的空间是三维的(x,y,z)，x、y、z分别是原始空间的三个基，我们可以通过某种方法，用新的坐标系(a,b,c)来表示原始的数据，那么a、b、c就是新的基，它们组成新的特征空间。在新的特征空间中，可能所有的数据在c上的投影都接近于0，即可以忽略，那么我们就可以直接用(a,b)来表示数据，这样数据就从三维的(x,y,z)降到了二维的(a,b)。
问题是如何求新的基(a,b,c)?
一般步骤是这样的：
1）对原始数据集做标准化处理。
2）求协方差矩阵。
3）计算协方差矩阵的特征值和特征向量。
4）选择前k个最大的特征向量，k小于原数据集维度。
5）通过前k个特征向量组成了新的特征空间，设为W。
6)通过矩阵W,把原数据转换到新的k维特征子空间。

17.2 PCA算法实现

这里以葡萄酒数据为例，数据集特征如下：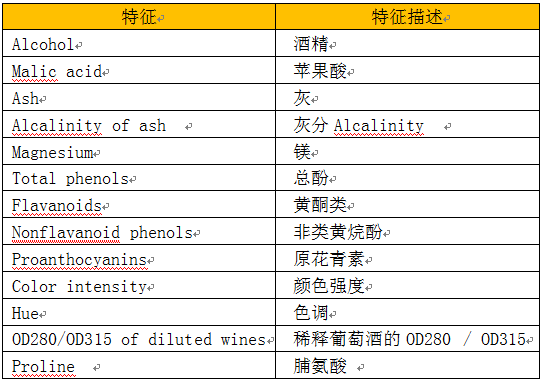

数据来源于：https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
1）对原数据集做标准化处理
导入需要的库及数据

 

 

 

1 2 3 4 5 6 7 8 9 10	import pandas as pd   df_wine = pd.read_csv(‘https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data‘, header=None)   df_wine.columns = [‘Class label‘, ‘Alcohol‘, ‘Malic acid‘, ‘Ash‘, ‘Alcalinity of ash‘, ‘Magnesium‘, ‘Total phenols‘, ‘Flavanoids‘, ‘Nonflavanoid phenols‘, ‘Proanthocyanins‘, ‘Color intensity‘, ‘Hue‘, ‘OD280/OD315 of diluted wines‘, ‘Proline‘]   df_wine.head()

部分内容：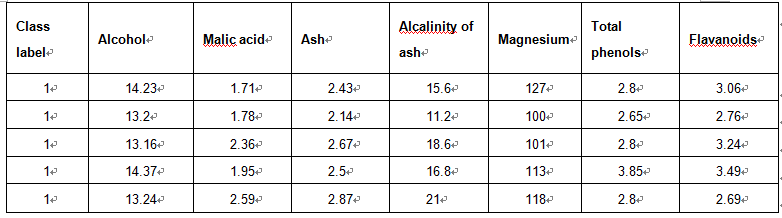

为便于后续处理，把数据集分为训练集和测试集，划分比例为7:3

 

1 2 3 4 5

from sklearn.cross_validation import train_test_split   X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values X_train, X_test, y_train, y_test =         train_test_split(X, y, test_size=0.3, random_state=0)

对原数据进行标准化处理

 

1 2 3 4 5

from sklearn.preprocessing import StandardScaler   sc = StandardScaler() X_train_std = sc.fit_transform(X_train) X_test_std = sc.fit_transform(X_test)

2) 求协方差矩阵
这里使用numpy.cov函数，求标准化后数据的协方差矩阵

 

1 2	import numpy as np cov_mat = np.cov(X_train_std.T)

3）计算协方差矩阵的特征值和特征向量
使用np.linalg.eig函数，求协方差的特征值和特征向量

 

1 2	eigen_vals, eigen_vecs = np.linalg.eig(cov_mat) print(‘ Eigenvalues %s‘ % eigen_vals)

得到13个特征向量：
Eigenvalues
[ 4.8923083 2.46635032 1.42809973 1.01233462 0.84906459 0.60181514 0.52251546 0.08414846 0.33051429 0.29595018 0.16831254 0.21432212 0.2399553 ]
要实现降维，我们可以选择前k个最多信息（或方差最大）特征向量组成新的子集，由于特征值的大小决定了特征向量的重要性，因此，可以通过对特征值的排序，获取前k个特征值。特征值λ_i的方差贡献率是指特征值λ_i与所有特征值和的比例：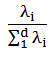

我们可以通过numpy.cumsum函数计算累计方差。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

tot = sum(eigen_vals) var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)] cum_var_exp = np.cumsum(var_exp)   #然后用matplotlib各主成分的方差贡献率图形。   import matplotlib.pyplot as plt %matplotlib inline   import matplotlib.font_manager as fm myfont = fm.FontProperties(fname=‘/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf‘)   plt.bar(range(1, 14), var_exp, alpha=0.5, align=‘center‘,         label=‘individual explained variance‘) plt.step(range(1, 14), cum_var_exp, where=‘mid‘,          label=‘cumulative explained variance‘) plt.ylabel(‘方差贡献率‘,fontproperties=myfont,size=12) plt.xlabel(‘主成分‘,fontproperties=myfont,size=12) plt.legend(loc=‘best‘) plt.tight_layout() plt.show()

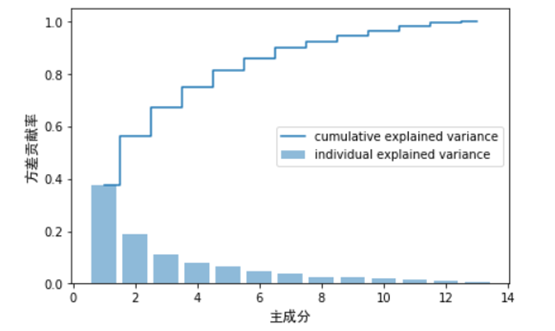
从这个图可以看出第一个主成分占了方差总和的40%左右，前两个主成分占了近60%。
4）选择前k个最大的特征向量，k小于原数据集维度
首先，按特征值按降序排序

 

1 2 3 4 5

# 构成一个元组 (eigenvalue, eigenvector) eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]   # Sort the (eigenvalue, eigenvector) tuples from high to low eigen_pairs.sort(reverse=True)

5）通过前k个特征向量组成了新的特征空间，设为W。
为便于数据可视化，这里我们取k=2，实际上前2个特征值已占了总方差的近60%。

 

1 2 3

w = np.hstack((eigen_pairs[0][1][:, np.newaxis],                eigen_pairs[1][1][:, np.newaxis])) print(‘Matrix W: ‘, w)

这样我们就可得到一个由这两个特征向量构成的13*2矩阵W:
Matrix W:
[[ 0.14669811 0.50417079]
[-0.24224554 0.24216889]
[-0.02993442 0.28698484]
[-0.25519002 -0.06468718]
[ 0.12079772 0.22995385]
[ 0.38934455 0.09363991]
[ 0.42326486 0.01088622]
[-0.30634956 0.01870216]
[ 0.30572219 0.03040352]
[-0.09869191 0.54527081]
[ 0.30032535 -0.27924322]
[ 0.36821154 -0.174365 ]
[ 0.29259713 0.36315461]]

6）通过矩阵W,把原数据转换到新的k维特征子空间
通过这个特征矩阵W,把原样本x转换到PCA的子空间上，得到一个新样本x^，。
x^，=xW
训练集与W点积后，把这个训练集转换到包括两个主成分的子空间上。然后，把子空间的数据可视化。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14

X_train_pca = X_train_std.dot(w) colors = [‘r‘, ‘b‘, ‘g‘] markers = [‘s‘, ‘x‘, ‘o‘]   for l, c, m in zip(np.unique(y_train), colors, markers):     plt.scatter(X_train_pca[y_train==l, 0],                 X_train_pca[y_train==l, 1],                 c=c, label=l, marker=m)   plt.xlabel(‘PC 1‘) plt.ylabel(‘PC 2‘) plt.legend(loc=‘lower left‘) plt.tight_layout() plt.show()

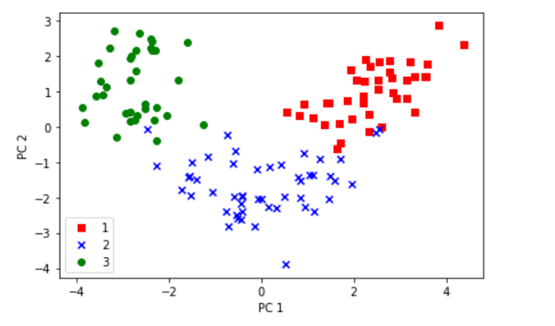
从以上图形可以看出，大部分数据沿PC1方向分布，而且可以线性划分，在可视化图形时，为便于标识点，这里采用了y_train标签信息。

我们用来6步来实现PCA，这个过程还是比较麻烦的，是否有更简单的方法呢？
有的，接下来我们介绍利用Scikit-learn中PCA类进行降维。

17.3 利用Scikit-learn进行主成分分析

我们将使用Scikit-learn中PCA对数据集进行预测处理，然后使用逻辑斯谛回归对转换后的数据进行分类，最后对数据进行可视化。
1）数据预处理

 

1 2 3 4 5

from sklearn.decomposition import PCA   pca = PCA() X_train_pca = pca.fit_transform(X_train_std) pca.explained_variance_ratio_

得到主成分数据：
array([ 0.37329648, 0.18818926, 0.10896791, 0.07724389, 0.06478595, 0.04592014, 0.03986936, 0.02521914, 0.02258181, 0.01830924, 0.01635336, 0.01284271, 0.00642076])

2）可视化主成分方差贡献率图

 

1 2 3 4 5

plt.bar(range(1, 14), pca.explained_variance_ratio_, alpha=0.5, align=‘center‘) plt.step(range(1, 14), np.cumsum(pca.explained_variance_ratio_), where=‘mid‘) plt.ylabel(‘Explained variance ratio‘) plt.xlabel(‘Principal components‘) plt.show()

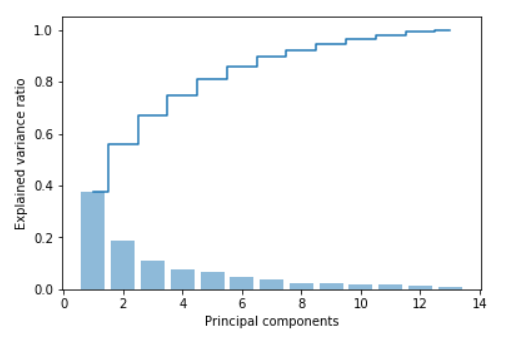
3）获取前2个主成分

 

1 2 3 4 5 6 7 8

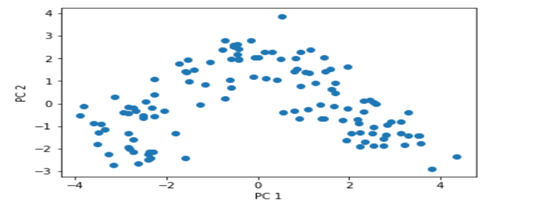
pca = PCA(n_components=2) X_train_pca = pca.fit_transform(X_train_std) X_test_pca = pca.transform(X_test_std) 4）把训练集映射到主成分空间上，并可视化。 plt.scatter(X_train_pca[:,0], X_train_pca[:,1]) plt.xlabel(‘PC 1‘) plt.ylabel(‘PC 2‘) plt.show()

5）利用回归模型对数据进行分类。

 

1 2 3 4

from sklearn.linear_model import LogisticRegression   lr = LogisticRegression() lr = lr.fit(X_train_pca, y_train)

6）为了更好看到分类后情况，这里我们定义一个函数plot_decision_regions，通过这个函数对决策区域数据可视化。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

from matplotlib.colors import ListedColormap def plot_decision_regions(X, y, classifier, resolution=0.02):       # setup marker generator and color map     markers = (‘s‘, ‘x‘, ‘o‘, ‘^‘, ‘v‘)     colors = (‘red‘, ‘blue‘, ‘lightgreen‘, ‘gray‘, ‘cyan‘)     cmap = ListedColormap(colors[:len(np.unique(y))])       # plot the decision surface     x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1     x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1     xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),                          np.arange(x2_min, x2_max, resolution))     Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)     Z = Z.reshape(xx1.shape)     plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)     plt.xlim(xx1.min(), xx1.max())     plt.ylim(xx2.min(), xx2.max())       # plot class samples     for idx, cl in enumerate(np.unique(y)):         plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],                     alpha=0.8, c=cmap(idx),                     marker=markers[idx], label=cl)

7)把训练数据转换到前两个主成分轴后生成决策区域图形

 

1 2 3 4 5 6 7

plot_decision_regions(X_train_pca, y_train, classifier=lr) plt.xlabel(‘PC 1‘) plt.ylabel(‘PC 2‘) plt.legend(loc=‘lower left‘) plt.tight_layout() # plt.savefig(‘./figures/pca3.png‘, dpi=300) plt.show()

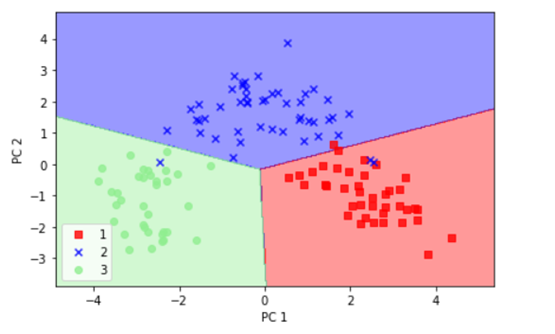
对高维数据集进行降维除了PCA方法，还有线性判别分析（Linear Discriminant Analysis， LDA）、决策树、核主成分分析、SVD等等。

17.4 LDA 降维

LDA的基本概念与PCA类似，PCA是在数据集中找到方差最大的正交的主成分分量的轴。而LDA的目标是发现可以最优化分类的特征子空间。两者都是可以用于降维的线性转换方法，其中，PCA是无监督算法，LDA是监督算法。与PCA相比，LDA是一种更优越的用于分类的特征提取技术。
LDA的主要步骤：
（1）对d维数据集进行标准化处理（d为特征数量）
（2）对每一类别，计算d维的均值向量
（3）构造类间的散布矩阵S_B以及类内的散布矩阵S_W
（4）计算矩阵〖S_W〗^(-1) S_B的特征值所对应的特征向量，
（5）选取前k个特征值对应的特征向量，构造一个d x k维的转换矩阵W，其中特征向量以列的形式排列
（6）使用转换矩阵W将样本映射到新的特征子空间上.
以下还是以下葡萄酒数据为例，用代码实现以上各步：
（1）对d维数据集进行标准化处理

 

1 2 3 4 5 6 7 8

from sklearn.preprocessing import StandardScaler   X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) #对特征进行标准化处理 sc = StandardScaler() X_train_std = sc.fit_transform(X_train) X_test_std = sc.transform(X_test)

（2）对每一类别，计算d维的均值向量

 

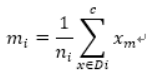
1 2 3 4 5 6 7 8

#设置精度 np.set_printoptions(precision=4)   #求各类的平均值 mean_vecs = [] for label in range(1,4):     mean_vecs.append(np.mean(X_train_std[y_train==label], axis=0))     print(‘MV %s: %s ‘ %(label, mean_vecs[label-1]))

运行结果
MV 1: [ 0.9259 -0.3091 0.2592 -0.7989 0.3039 0.9608 1.0515 -0.6306 0.5354 0.2209 0.4855 0.798 1.2017]

MV 2: [-0.8727 -0.3854 -0.4437 0.2481 -0.2409 -0.1059 0.0187 -0.0164 0.1095 -0.8796 0.4392 0.2776 -0.7016]

MV 3: [ 0.1637 0.8929 0.3249 0.5658 -0.01 -0.9499 -1.228 0.7436 -0.7652 0.979 -1.1698 -1.3007 -0.3912]
（3）构造类间的散布矩阵S_B以及类内的散布矩阵S_W
通过均值向量计算类内散布矩阵Sw：

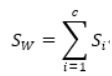
通过累加各类别i的散布矩阵Si来计算：

 

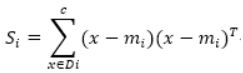
1 2 3 4 5 6 7 8 9 10

d = 13 # number of features S_W = np.zeros((d, d)) for label,mv in zip(range(1, 4), mean_vecs):     class_scatter = np.zeros((d, d)) # scatter matrix for each class     for row in X_train_std[y_train == label]:         row, mv = row.reshape(d, 1), mv.reshape(d, 1) # make column vectors         class_scatter += (row-mv).dot((row-mv).T)     S_W += class_scatter                             # sum class scatter matrices   print(‘Within-class scatter matrix: %sx%s‘ % (S_W.shape[0], S_W.shape[1]))

运行结果
Within-class scatter matrix: 13x13

计算各类标样本数

 

1	print(‘Class label distribution: %s‘ % np.bincount(y_train)[1:])

运行结果为：
Class label distribution: [40 49 35]
由此看出，各类记录数不很均匀，为此，需要对SB进行归一化处理：

 

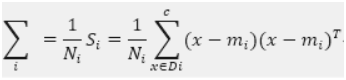
1 2 3 4 5 6

d = 13 # number of features S_W = np.zeros((d, d)) for label,mv in zip(range(1, 4), mean_vecs):     class_scatter = np.cov(X_train_std[y_train==label].T)     S_W += class_scatter print(‘Scaled within-class scatter matrix: %sx%s‘ % (S_W.shape[0], S_W.shape[1]))

运行结果
Scaled within-class scatter matrix: 13x13

计算类间散布矩阵：

 

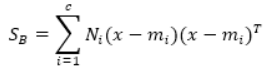
1 2 3 4 5 6 7 8 9 10

mean_overall = np.mean(X_train_std, axis=0) d = 13 # number of features S_B = np.zeros((d, d)) for i,mean_vec in enumerate(mean_vecs):     n = X_train[y_train==i+1, :].shape[0]     mean_vec = mean_vec.reshape(d, 1) # make column vector     mean_overall = mean_overall.reshape(d, 1) # make column vector     S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)   print(‘Between-class scatter matrix: %sx%s‘ % (S_B.shape[0], S_B.shape[1]))

运行结果
Between-class scatter matrix: 13x13

 

1	eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))

（5）选取前k个特征值对应的特征向量，构造一个d x k维的转换矩阵W，其中特征向量以列的形式排列

求得广义特征值之后，按照降序对特征值排序

 

1 2 3 4 5 6 7 8 9 10 11

# 生成特征值与特征向量构成的元组 eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]   # Sort the (eigenvalue, eigenvector) tuples from high to low eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)   # Visually confirm that the list is correctly sorted by decreasing eigenvalues   print(‘Eigenvalues in decreasing order: ‘) for eigen_val in eigen_pairs:     print(eigen_val[0])

运行结果
Eigenvalues in decreasing order:

452.721581245
156.43636122
7.05575044266e-14
5.68434188608e-14
3.41129233161e-14
3.40797229523e-14
3.40797229523e-14
1.16775565372e-14
1.16775565372e-14
8.59477909861e-15
8.59477909861e-15
4.24523361436e-15
2.6858909629e-15
d x d维协方差矩阵的秩最大为d-1，得到两个非0的特征值。
与PCA一样，我们可视化各特征贡献率

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

tot = sum(eigen_vals.real) discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)] cum_discr = np.cumsum(discr)   plt.bar(range(1, 14), discr, alpha=0.5, align=‘center‘,         label=‘individual "discriminability"‘) plt.step(range(1, 14), cum_discr, where=‘mid‘,          label=‘cumulative "discriminability"‘) plt.ylabel(‘"discriminability" ratio‘) plt.xlabel(‘Linear Discriminants‘) plt.ylim([-0.1, 1.1]) plt.legend(loc=‘best‘) plt.tight_layout() # plt.savefig(‘./figures/lda1.png‘, dpi=300) plt.show()

运行结果

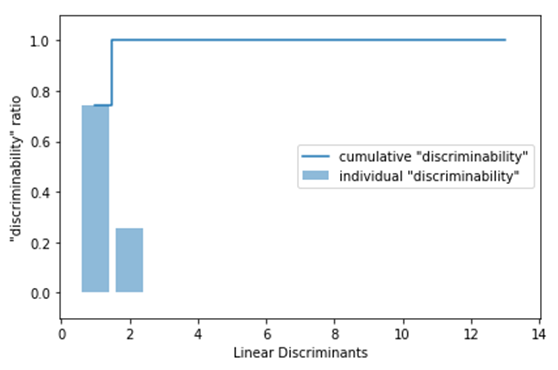
（6）使用转换矩阵W将样本映射到新的特征子空间上.
由上面两个新得到两个特征构成一个新矩阵

 

1 2 3

w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,                       eigen_pairs[1][1][:, np.newaxis].real)) print(‘Matrix W: ‘, w)

d x d维协方差矩阵的秩最大为d-1，得到两个非0的特征值。Matrix W:
[[-0.0662 -0.3797]
[ 0.0386 -0.2206]
[-0.0217 -0.3816]
[ 0.184 0.3018]
[-0.0034 0.0141]
[ 0.2326 0.0234]
[-0.7747 0.1869]
[-0.0811 0.0696]
[ 0.0875 0.1796]
[ 0.185 -0.284 ]
[-0.066 0.2349]
[-0.3805 0.073 ]
[-0.3285 -0.5971]]
将样本映射到新的特征空间

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

X_train_lda = X_train_std.dot(w) colors = [‘r‘, ‘b‘, ‘g‘] markers = [‘s‘, ‘x‘, ‘o‘]   for l, c, m in zip(np.unique(y_train), colors, markers):     plt.scatter(X_train_lda[y_train==l, 0] * (-1),                 X_train_lda[y_train==l, 1] * (-1),                 c=c, label=l, marker=m)   plt.xlabel(‘LD 1‘) plt.ylabel(‘LD 2‘) plt.legend(loc=‘lower right‘) plt.tight_layout() # plt.savefig(‘./figures/lda2.png‘, dpi=300) plt.show()

运行结果

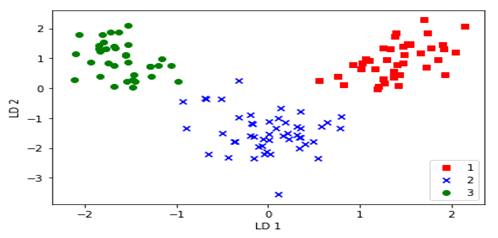
17.5 利用Scikit-learn进行LDA分析

下面我们利用scikit-learn中对LDA类的实现
这里先定义一个函数，后面需要用到

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

from matplotlib.colors import ListedColormap   def plot_decision_regions(X, y, classifier, resolution=0.02):       # setup marker generator and color map     markers = (‘s‘, ‘x‘, ‘o‘, ‘^‘, ‘v‘)     colors = (‘red‘, ‘blue‘, ‘lightgreen‘, ‘gray‘, ‘cyan‘)     cmap = ListedColormap(colors[:len(np.unique(y))])       # plot the decision surface     x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1     x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1     xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),                          np.arange(x2_min, x2_max, resolution))     Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)     Z = Z.reshape(xx1.shape)     plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)     plt.xlim(xx1.min(), xx1.max())     plt.ylim(xx2.min(), xx2.max())       # plot class samples     for idx, cl in enumerate(np.unique(y)):         plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],                     alpha=0.8, c=cmap(idx),                     marker=markers[idx], label=cl)

对数据先LDA处理，然后用逻辑回归进行分类。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA     lda = LDA(n_components=2) X_train_lda = lda.fit_transform(X_train_std, y_train) # 逻辑回归在相对低维数据上的表现 from sklearn.linear_model import LogisticRegression lr = LogisticRegression() lr = lr.fit(X_train_lda, y_train)   plot_decision_regions(X_train_lda, y_train, classifier=lr) plt.xlabel(‘LD 1‘) plt.ylabel(‘LD 2‘) plt.legend(loc=‘lower left‘) plt.tight_layout() # plt.savefig(‘./images/lda3.png‘, dpi=300) plt.show()

运行结果

还有几个点划分错误，下面通过正则化，效果将更好

 

1 2 3 4 5 6 7 8 9

X_test_lda = lda.transform(X_test_std)   plot_decision_regions(X_test_lda, y_test, classifier=lr) plt.xlabel(‘LD 1‘) plt.ylabel(‘LD 2‘) plt.legend(loc=‘lower left‘) plt.tight_layout() # plt.savefig(‘./images/lda4.png‘, dpi=300) plt.show()

运行结果

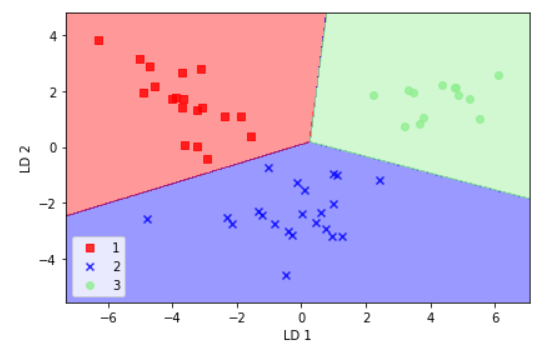
17.6使用核PCA降维

前面我们介绍了两种降维方法，PCA及LDA.这两种方法，如果用于线性不可分数据集上进行分类，效果往往不很理想，原因是通过他们无法把线性不可分数据集变为线性可分数据集。如果遇到线性不可分数据集（这样的数据集往往比较普遍），有什么好方法，既降维，又可把线性不可分数据集变为线性可分数据集？
在SVM中，我们了解到核函数的神奇，把可以通过把线性不可分的数据集映射到一个高维空间，变得线性可分。基于这点，如果我们在降维时也采用核技术是否也可以呢？可以的，这就是接下来我们要介绍的内容---核PCA.
核PCA=核技术+PCA,具体步骤如下：
（1）计算核矩阵，也就是计算任意两个训练样本。这里以向基核函数（RBF）为例
经向基函数核（又称高斯核）为：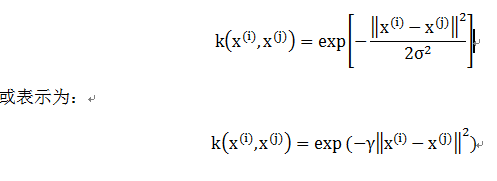

得到以下矩阵：

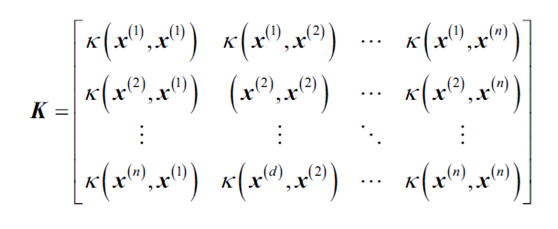
（2）对核矩阵K进行中心化处理

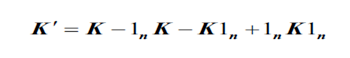
其中,是n*n的矩阵，n=训练集样本数，中每个元素都等于.l_n中的每个元素都是1/n
（3）求核矩阵的特征向量，并按降序排列，提取前k个特征向量。
不同于标准PCA，这里的特征向量并不是主成分轴。
下面我们根据以上三个步骤，实现一个核PCA。借助SciPy和NumPy，其实实现核PCA很简单。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

from scipy.spatial.distance import pdist, squareform from scipy import exp from scipy.linalg import eigh import numpy as np   def rbf_kernel_pca(X, gamma, n_components):     """     RBF kernel PCA implementation.       Parameters     ------------     X: {NumPy ndarray}, shape = [n_samples, n_features]              gamma: float       Tuning parameter of the RBF kernel              n_components: int       Number of principal components to return       Returns     ------------      X_pc: {NumPy ndarray}, shape = [n_samples, k_features]        Projected dataset         """     # Calculate pairwise squared Euclidean distances     # in the MxN dimensional dataset.     sq_dists = pdist(X, ‘sqeuclidean‘)       # Convert pairwise distances into a square matrix.     mat_sq_dists = squareform(sq_dists)       # Compute the symmetric kernel matrix.     K = exp(-gamma * mat_sq_dists)       # Center the kernel matrix.     N = K.shape[0]     one_n = np.ones((N,N)) / N     K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)       # Obtaining eigenpairs from the centered kernel matrix     # numpy.eigh returns them in sorted order     eigvals, eigvecs = eigh(K)       # Collect the top k eigenvectors (projected samples)     X_pc = np.column_stack((eigvecs[:, -i]                             for i in range(1, n_components + 1)))       return X_pc

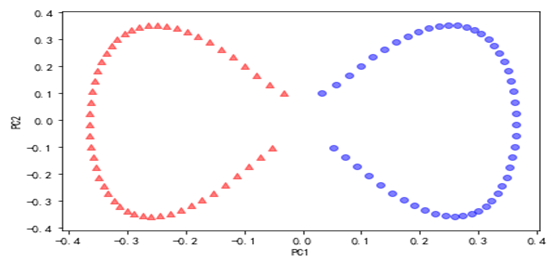
下面以一分离同心数据集为例，分别用PCA和核PCA对数据集进行处理，然后处理后的结果，具体请看以下代码及生成的图形：

 

1 2 3 4 5 6 7 8 9

from sklearn.datasets import make_circles   X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)   plt.scatter(X[y==0, 0], X[y==0, 1], color=‘red‘, marker=‘^‘, alpha=0.5) plt.scatter(X[y==1, 0], X[y==1, 1], color=‘blue‘, marker=‘o‘, alpha=0.5)   plt.tight_layout() plt.show()

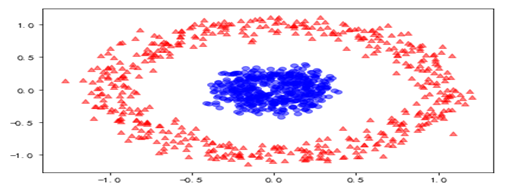
这是典型线性不可数据集，现在我们分别用PCA及核PCA进行处理。
（1）用PCA处理，然后进行分类

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler import matplotlib.pyplot as plt   scikit_pca = PCA(n_components=2) X_spca = scikit_pca.fit_transform(X)   plt.figure( figsize=(5,3))   plt.scatter(X_spca[y==0, 0], X_spca[y==0, 1],             color=‘red‘, marker=‘^‘, alpha=0.5) plt.scatter(X_spca[y==1, 0], X_spca[y==1, 1],             color=‘blue‘, marker=‘o‘, alpha=0.5)     plt.xlabel(‘PC1‘) plt.ylabel(‘PC2‘)   plt.show()

（2）用核PCA处理，然后进行分类

 

1 2 3 4 5 6 7 8 9 10 11 12

X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)   plt.figure( figsize=(5,3)) plt.scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],             color=‘red‘, marker=‘^‘, alpha=0.5) plt.scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],             color=‘blue‘, marker=‘o‘, alpha=0.5)   plt.xlabel(‘PC1‘) plt.ylabel(‘PC2‘)   plt.show()

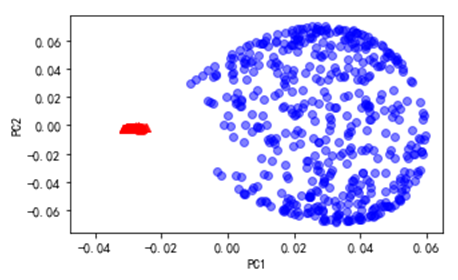
（3）使用sklearn实现核PCA
源数据的图形为

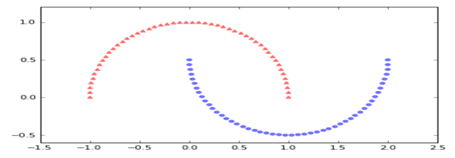
这里通过核PCA把该数据变为线性可分数据集，实现代码如下：

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

from sklearn.decomposition import KernelPCA from sklearn.datasets import make_moons   X, y = make_moons(n_samples=100, random_state=123) scikit_kpca = KernelPCA(n_components=2, kernel=‘rbf‘, gamma=15) X_skernpca = scikit_kpca.fit_transform(X)   plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1],             color=‘red‘, marker=‘^‘, alpha=0.5) plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1],             color=‘blue‘, marker=‘o‘, alpha=0.5)   plt.xlabel(‘PC1‘) plt.ylabel(‘PC2‘) plt.tight_layout() plt.show()

 

17.7 SVD矩阵分解

（1）SVD奇异值分解的定义
假设有一个mxn矩阵，如果存在一个分解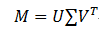

其中U为的mxm酉矩阵，∑为mxn的半正定对角矩阵，除了对角元素不为0，其他元素都为0，并且对角元素是从大到小排列的，前面的元素比较大，后面的很多元素接近0。这些对角元素就是奇异值。V^T为V的共轭转置矩阵，且为nxn的酉矩阵。这样的分解称为的奇异值分解，对角线上的元素称为奇异值，U称为左奇异矩阵，V^T称为右奇异矩阵。
SVD在信息检索（隐性语义索引）、图像压缩、推荐系统、金融等领域都有应用。
（2）SVD奇异值分解与特征值分解的关系
特征值分解与SVD奇异值分解的目的都是提取一个矩阵最重要的特征。然而，特征值分解只适用于方阵，而SVD奇异值分解适用于任意的矩阵，不一定是方阵。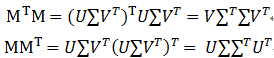

这里M^T M和MM^T都是方阵，UU^T和VV^T都是单位矩阵，V是M^T M的特征向量，U是MM^T的特征向量。
（3）SVD奇异值分解的作用和意义
奇异值分解最大的作用就是数据的降维，当然，还有其他很多的作用，这里主要讨论数据的降维，对于mxn的M矩阵，进行奇异值分解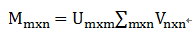

取其前k个非零奇异值，可以还原原来的矩阵，即前k个非零奇异值对应的奇异向量代表了矩阵的主要特征。可以表示为

17.8 用Python实现SVD，并用于图像压缩
（1）首先读取一张图片（128*128*3）：

 

1 2 3 4 5 6 7 8 9 10 11 12 13

#!python #  -*- coding:utf-8 -*- from PIL import Image import os import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt   if __name__ == ‘__main__‘:     mpl.rcParams[‘font.sans-serif‘] = [u‘simHei‘]     mpl.rcParams[‘axes.unicode_minus‘] = False     A = Image.open(‘02.jpg‘)     a = np.array(A)  #转换成矩阵

（2）然后可以利用python的numpy库对彩色图像的3个通道进行SVD分解

 

1 2 3 4 5

numpy库中有SVD分解函数：np.linalg.svd #由于是彩色图像，所以3通道。a的最内层数组为三个数，分别表示RGB，用来表示一个像素 u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0]) u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1]) u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2])

（3）然后便可以根据需要压缩图像（丢弃分解出来的三个矩阵中的数据），利用的奇异值个数越少，则压缩的越厉害。下面来看一下不同程度压缩后，重构图像的清晰度：

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

plt.figure(facecolor = ‘w‘, figsize = (10, 10)) # 奇异值个数依次取：1,2,...,16。来看看一下效果 K = 16 for k in range(1, K + 1):     R = restore(u_r, sigma_r, v_r, k)     G = restore(u_g, sigma_g, v_g, k)     B = restore(u_b, sigma_b, v_b, k)     I = np.stack((R, G, B), axis = 2)     # 将图片重构后的显示出来     plt.subplot(4, 4, k)     plt.imshow(I)     plt.axis(‘off‘)     plt.title(u‘奇异值个数：%d‘ %  k)   plt.suptitle(u‘SVD与图像分解‘, fontsize = 20) plt.tight_layout(0.1, rect = (0, 0, 1, 0.92)) plt.show()

（4）其中restore函数定义为

 

1 2 3 4 5 6 7 8 9 10 11 12 13

def restore(u, sigma, v, k):     m = len(u)     n = len(v)     a = np.zeros((m, n))     # 重构图像     a = np.dot(u[:, :k], np.diag(sigma[:k])).dot(v[:k, :])     # 上述语句等价于：     # for i in range(k):     #     ui = u[:, i].reshape(m, 1)     #     vi = v[i].reshape(1, n)     #     a += sigma[i] * np.dot(ui, vi)     a[a < 0] = 0 a[a > 255] = 255     return np.rint(a).astype(‘uint8‘)