视频+图文+动画 详解插入排序(轻松易理解系列)
Posted qpgshare
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了视频+图文+动画 详解插入排序(轻松易理解系列)相关的知识,希望对你有一定的参考价值。
一、视频讲解插入排序
二、插入排序的思想
- 把n个待排序的元素看成是一个有序表和一个无序表
- 第一轮排序时,有序表中只含一个元素,无序表中包含n-1个元素
- 排序过程中,每次从无序表中取出第一个元素,去和有序表中的每个元素进行比较
- 找到适合自己的位置并插入,使自己成为有序表
三、插入排序的动画演示及思路分析
动画演示:
橙色的数字:有序表中的数字
粉色的数字:每轮无序表的第一个数
绿色的数字:有序表中需与无序表粉色数字进行比较的数
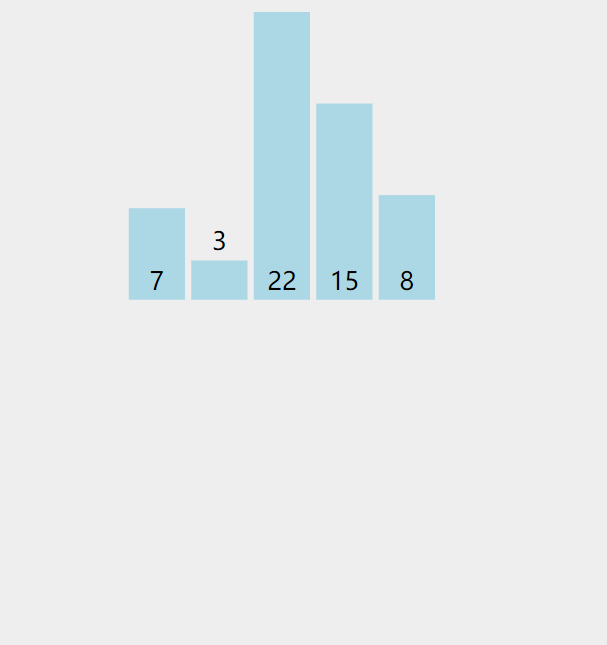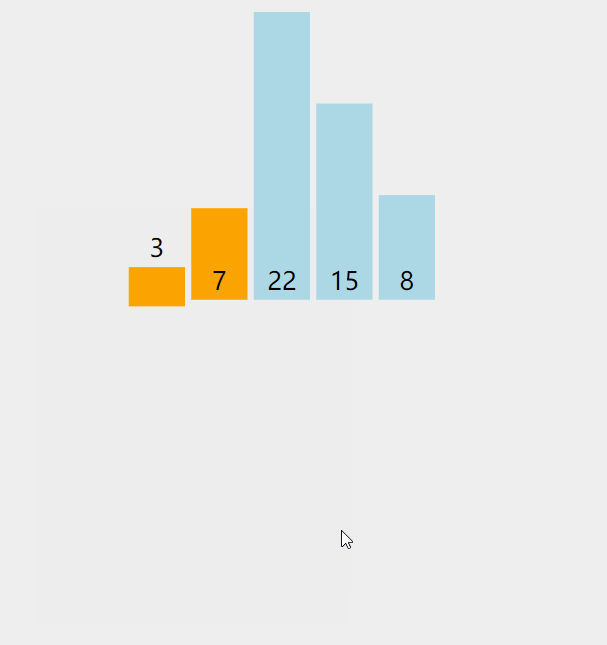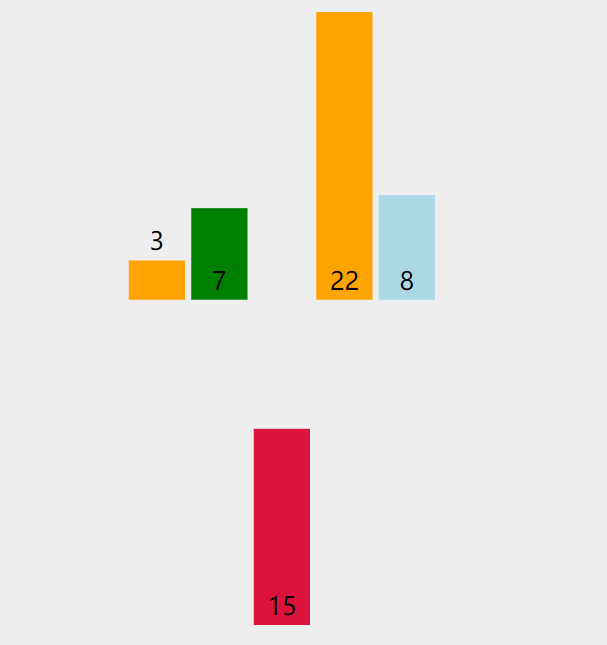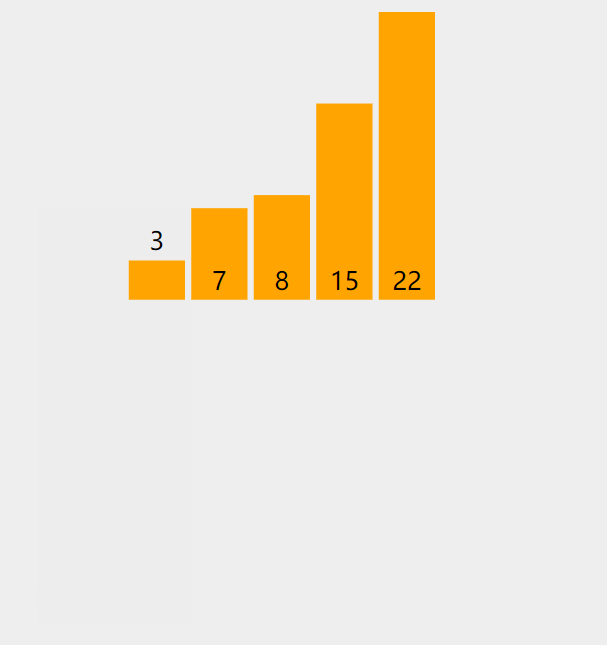
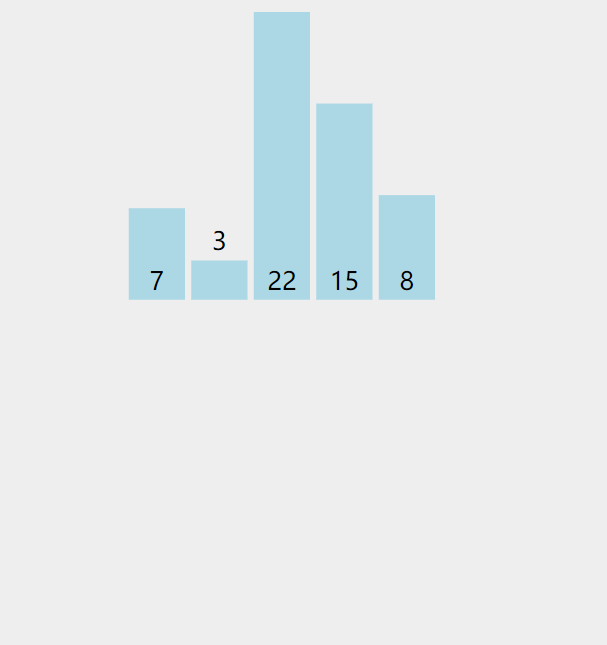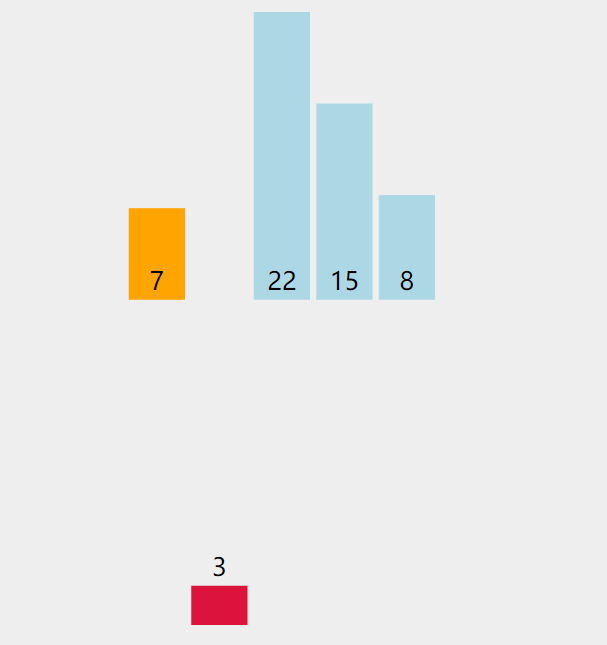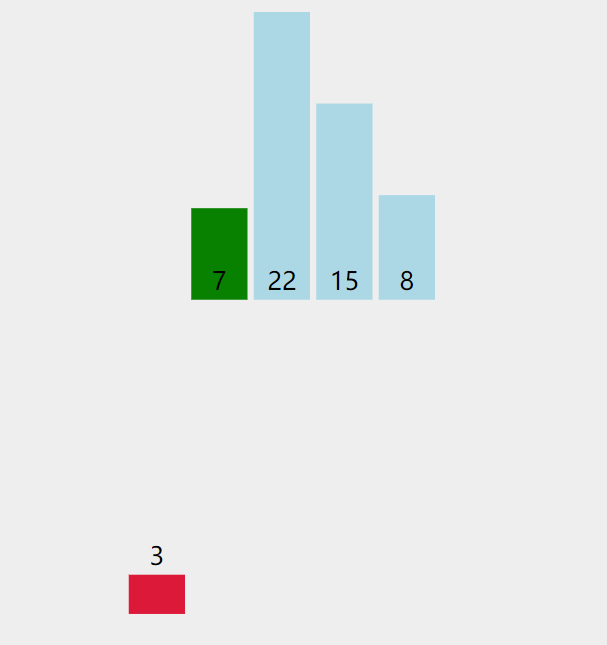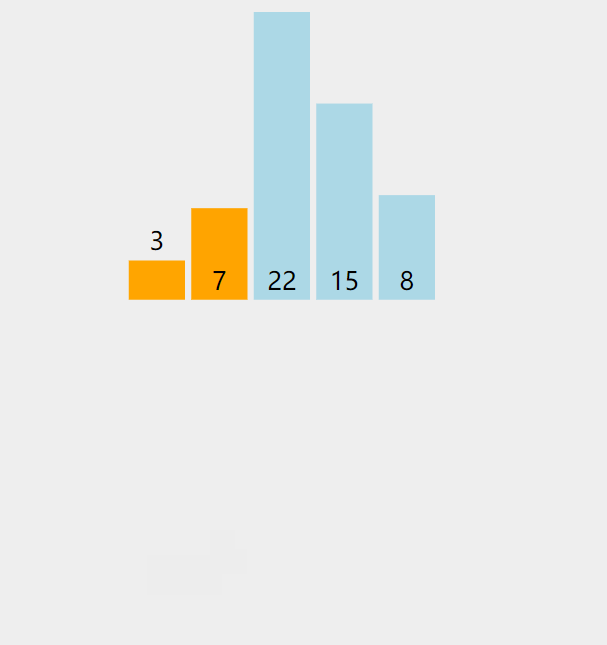
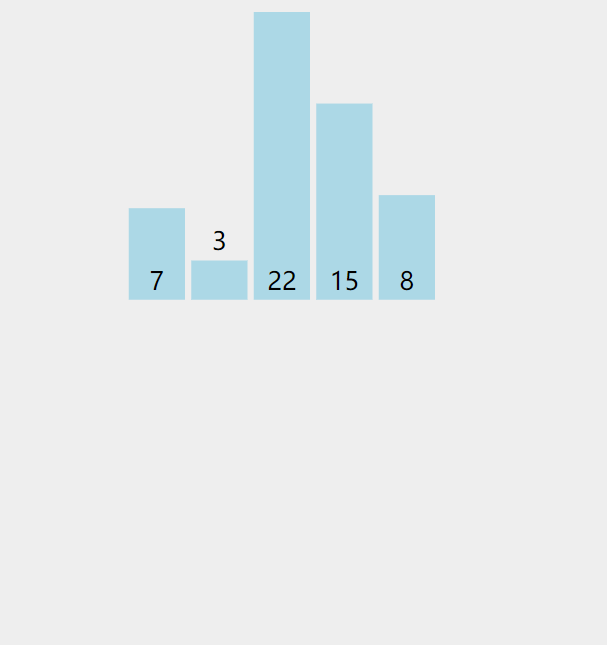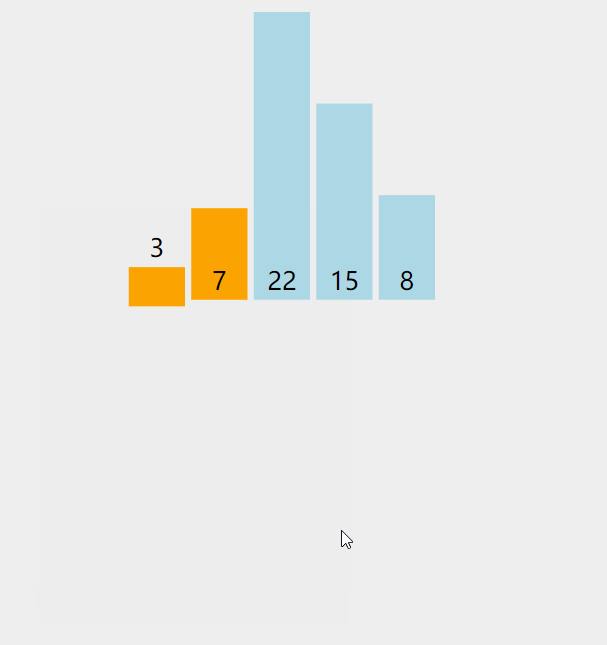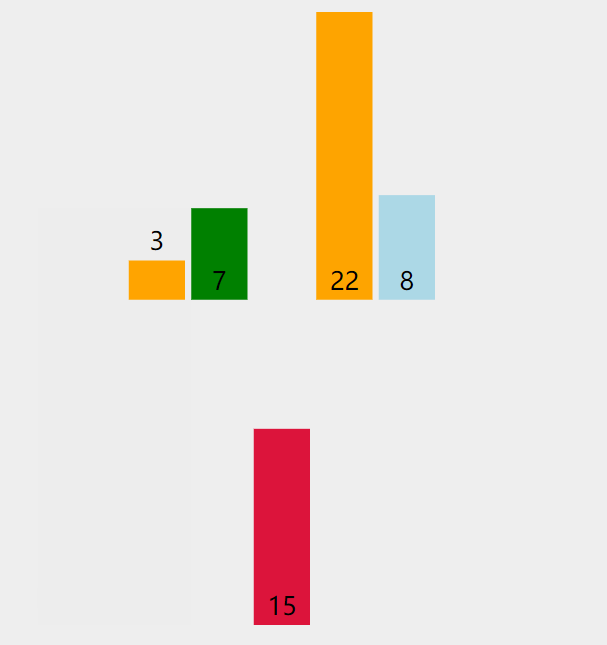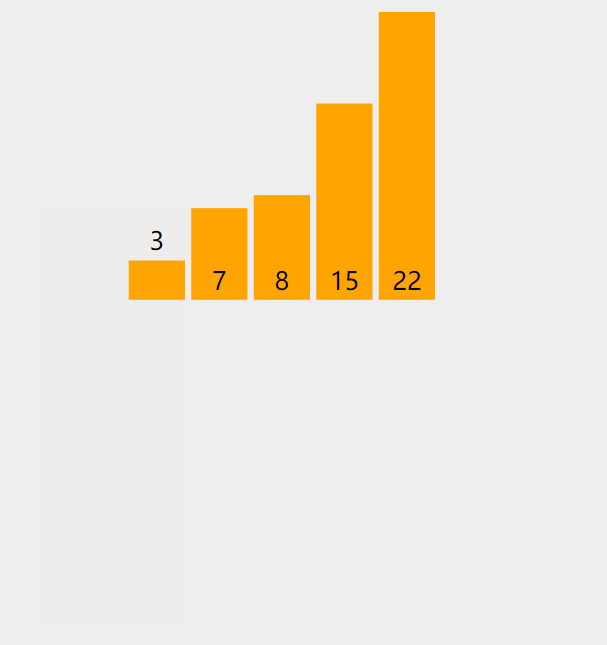
思路分析:以7,3,22,15,8为例
为了便于理解代码,在这里我们需用两个变量:
- insertValue:每轮排序中无序表中的第一个数字即待插入的数
- insertIndex:从此数组下标开始,为insertValue找合适的位置 【下标需要大于等于0的条件要遵守】
第一次排序:拿出无序表中的第1个元素3,与有序表的元素7进行比较
原始数组:7,3,22,15,8
| 有序表:7 | insertIndex:1-1=0 (从此下标开始往前找合适的位置) |
|---|---|
| 无序表:3,22,15,8 | insertValue (待插入的数):arr[1]–>3 |
- 3<7,所以arr[0]=7需要向后移一位,即arr[1]=7
- 此时3找到合适的位置【即下标为0的位置】,进行插入。
排序结果: 3,7,22,15,8
第二次排序:拿出无序表中的第1个元素22,与有序表的元素3,7进行比较
原始数组:3,7,22,15,8
| 有序表:3,7 | insertIndex:2-1=1 (从此下标开始往前找合适的位置) |
|---|---|
| 无序表:22,15,8 | insertValue (待插入的数):arr[2]–>22 |
- 22>7,所以22不需要移动,
- 此时22所在的位置就是其合适的位置【即下标为2的位置】。
排序结果: 3,7,22,15,8
第三次排序:拿出无序表中的第1个元素15,与有序表的元素3,7,22进行比较
原始数组:3,7,22,15,8
| 有序表:3,7,22 | insertIndex:3-1=2 (从此下标开始往前找合适的位置) |
|---|---|
| 无序表:15,8 | insertValue (待插入的数):arr[3]–>15 |

- 15<22,所以arr[2]=22需要向后移一位,即arr[3]=22
- 而15>7,所以此时15找到合适的位置【即下标为2的位置】,进行插入。
排序结果: 3,7,15,22,8
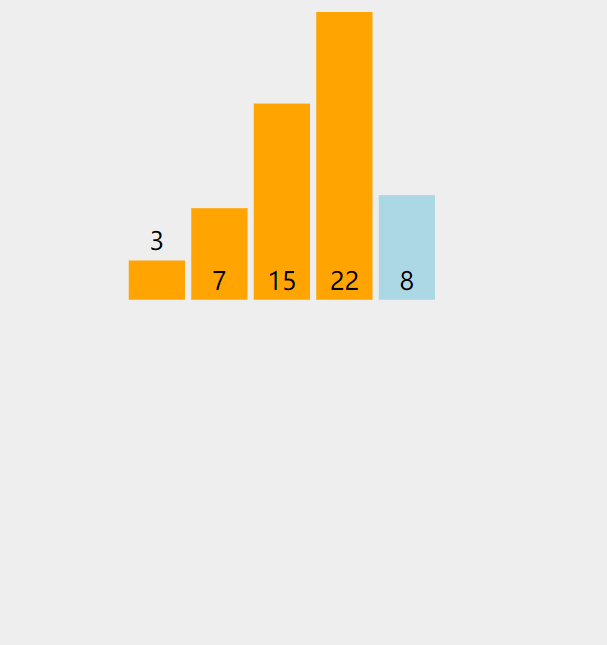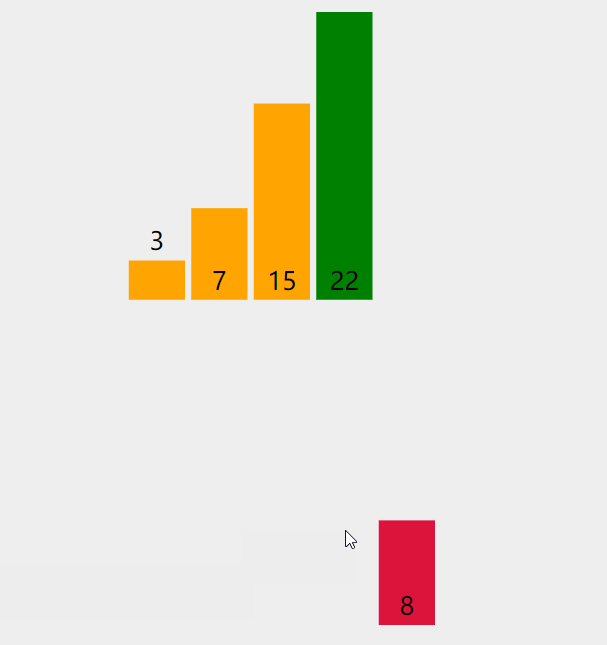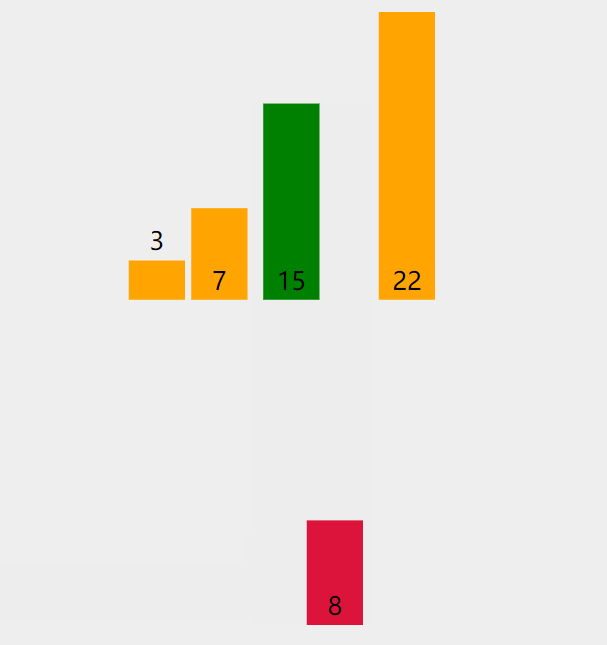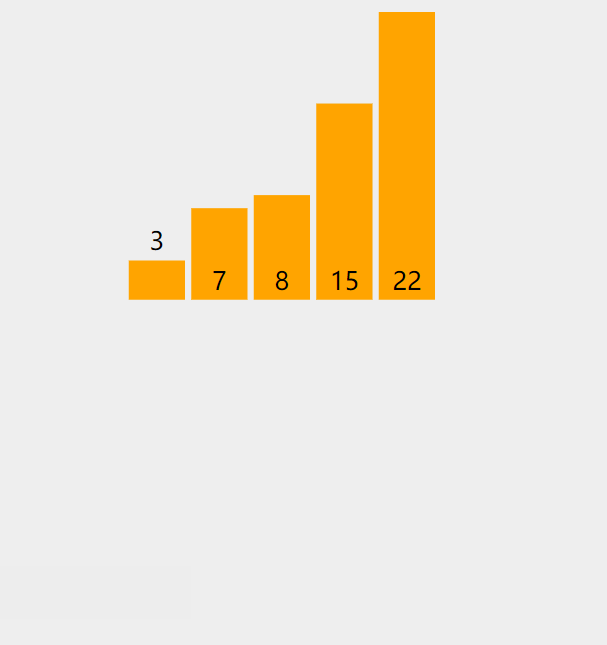
第四次排序:拿出无序表中的第1个元素8,与有序表的元素3,7,15,22进行比较
原始数组:3,7,15,22,8
| 有序表:3,7,15,,22 | insertIndex:4-1=3 (从此下标开始往前找合适的位置) |
|---|---|
| 无序表:8 | insertValue (待插入的数):arr[4]–>8 |
- 8<22,所以arr[3]=22需要向后移一位,即arr[4]=22
- 8<15,所以arr[2]=15需要向后移一位,即arr[3]=15
- 而8>7,所以此时8找到合适的位置【即下标为2的位置】,进行插入。
排序结果: 3,7,15,22,8
四、插入排序的代码+代码优化+代码详解
代码--————多个while循环分别控制排序:
package Sort;
import java.util.Arrays;
public class InsertSort {
public static void main(String[] args) {
int arr[] = { 7, 3, 22, 15, 8 };
int insertValue = 0; //(无序表的第一个值)待插入的值
int insertIndex = 0; //从这里开始查找待插入值的下标
//第一次排序
insertValue = 3;
insertIndex = 1-1;
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex]; //将7后移一个位置,arr[1]=7
insertIndex--;
}
//退出while循环,待插入的数的下标确定
arr[insertIndex + 1] = insertValue;
System.out.println("第一次排序的结果为:"+Arrays.toString(arr));
//第二次排序
insertValue = 22;
insertIndex = 2-1;
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
//退出while循环,待插入的数的下标确定
arr[insertIndex + 1] = insertValue;
System.out.println("第二次排序的结果为:"+Arrays.toString(arr));
//第三次排序
insertValue = 15;
insertIndex = 3-1;
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex]; //将22后移一个位置,arr[3]=22
insertIndex--;
}
//退出while循环,待插入的数的下标确定
arr[insertIndex + 1] = insertValue;
System.out.println("第三次排序的结果为:"+Arrays.toString(arr));
//第四次排序
insertValue = 8;
insertIndex = 4-1;
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
//将22后移一个位置即arr[4]=22;15也后移一个位置即arr[3]=15
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
//退出while循环,待插入的数的下标确定
arr[insertIndex + 1] = insertValue;
System.out.println("第四次排序的结果为:"+Arrays.toString(arr));
}
}
结果:
优化代码--————for循环嵌套while循环控制排序:
优化分析:
根据下表红色数据部分,我们可以看出:
- 可以用一个for循环嵌套在while循环外,控制1-4的变化
| insertValue:无序表中第一个数即待插入的数 | insertIndex:从此下标开始往前找合适的位置 | |
|---|---|---|
| 第一次排序 | arr[1]=3 | 1-1=0 |
| 第二次排序 | arr[2]=22 | 2-1=1(0-1) |
| 第三次排序 | arr[3]=15 | 3-1=2(0-2) |
| 第四次排序 | arr[4]=8 | 4-1=3(0-3) |
代码:
package Sort;
import java.util.Arrays;
public class InsertSort {
public static void main(String[] args) {
int arr[] = { 7, 3, 22, 15, 8 };
int insertValue = 0; //(无序表的第一个值)待插入的值
int insertIndex = 0; //从这里开始查找待插入值的下标
for (int i = 1; i < arr.length; i++) {
insertValue = arr[i];
insertIndex = i - 1;
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
//退出while循环,待插入的数的下标确定
if (insertIndex + 1 != i) {//如果insertIndex + 1 != i说明此数在正确位置上不用交换
arr[insertIndex + 1] = insertValue;
}
System.out.println("第" + i + "次排序的结果为:" + Arrays.toString(arr));
}
}
}
结果:
代码详解(优化版本):以7,3,22,15,8为例
第一次排序时:
- i=1,1<arr.length=5
- insertValue=arr[i]=arr[1]=3,
- insertIndex=i-1=1-1=0
- insertIndex=0且insertValue=3<arr[insertIndex]=7
满足while循环的条件while (insertIndex >= 0 && insertValue < arr[insertIndex])进入while循环
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
-
arr[insertIndex+1]=arr[insertIndex]即将原来arr[1]=3换为现在的arr[1]=7
7,3,22,15,8 -->7,3,22,15,8 --> 3,7,22,15,8
-
insertIndex--后InsertIndex=-1
不满足while循环条件,退出while循环,待插入数:3的位置找到即arr[0]=3 -
因为此时insertIndex=-1,满足
if (insertIndex + 1 != i)进入if分支语句
if (insertIndex + 1 != i) {//如果insertIndex + 1 != i说明此数在正确位置上不用交换
arr[insertIndex + 1] = insertValue;
}
-
所以arr[insertIndex+1]=insertValue 即arr[0]=3
-
输出第一次排序的结果:3,7,22,15,8 --> 3,7,22,15,8
第二次排序时:
- i=2,2<arr.length=5
- insertValue=arr[i]=arr[2]=22,
- insertIndex=i-1=2-1=1
- insertIndex=1但insertValue=22>arr[insertIndex]=7
不满足while循环的条件while (insertIndex >= 0 && insertValue < arr[insertIndex])不进入while循环
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
3,7,22,15,8 --> 3,7,22,15,8
- 因为此时insertIndex=1,不满足
if (insertIndex + 1 != i)不进入if分支语句
if (insertIndex + 1 != i) {//如果insertIndex + 1 != i说明此数在正确位置上不用交换
arr[insertIndex + 1] = insertValue;
}
-
所以本次排序不发生交换
-
输出第二次排序的结果:3,7,22,15,8 --> 3,7,22,15,8
第三次排序时:
- i=3,3<arr.length=5
- insertValue=arr[i]=arr[1]=3,
- insertIndex=i-1=3-1=2
- insertIndex=2且insertValue=15<arr[insertIndex]=22
满足while循环的条件while (insertIndex >= 0 && insertValue < arr[insertIndex])进入while循环
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
-
arr[insertIndex+1]=arr[insertIndex]即将原来arr[3]=15换为现在的arr[3]=22
3,7,22,15,8 --> 3,7,22,15,8 --> 3,7,22,22,8
-
insertIndex--后InsertIndex=1但insertValue=15>arr[insertIndex]=arr[1]=7
3,7,22,22,8 --> 3,7,22,22,8
不满足while循环条件,退出while循环,待插入数:15的位置找到即arr[2]=15
-
因为此时insertIndex=1,满足
if (insertIndex + 1 != i)进入if分支语句
if (insertIndex + 1 != i) {//如果insertIndex + 1 != i说明此数在正确位置上不用交换
arr[insertIndex + 1] = insertValue;
}
3,7,22,22,8 --> 3,7,15,22,8
-
所以arr[insertIndex+1]=insertValue 即arr[2]=15
-
输出第三次排序的结果:3,7,15,22,8
第四次排序时:
- i=4,4<arr.length=5
- insertValue=arr[i]=arr[4]=8,
- insertIndex=i-1=4-1=3
- insertIndex=3且insertValue=8<arr[insertIndex]=15
满足while循环的条件while (insertIndex >= 0 && insertValue < arr[insertIndex])进入while循环
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
-
arr[insertIndex+1]=arr[insertIndex]即将原来arr[3]=22换为现在的arr[4]=22
3,7,15,22,8 --> 3,7,15,22,8 --> 3,7,15,22,22
-
insertIndex--后InsertIndex=2且insertValue=8<arr[insertIndex]=arr[2]=15
满足while循环条件,进入while循环, -
arr[insertIndex+1]=arr[insertIndex]即将原来arr[3]=22换为现在的arr[3]=15
3,7,15,22,22 --> 3,7,15,22,22 --> 3,7,15,15,22
-
insertIndex--后InsertIndex=1但insertValue=8>arr[insertIndex]=arr[1]=7
不满足while循环条件,退出while循环,待插入数:8的位置找到即arr[2]=8 -
因为此时insertIndex=1,满足
if (insertIndex + 1 != i)进入if分支语句
if (insertIndex + 1 != i) {//如果insertIndex + 1 != i说明此数在正确位置上不用交换
arr[insertIndex + 1] = insertValue;
}
3,7,15,15,22 --> 3,7,8,15,22
-
所以arr[insertIndex+1]=insertValue 即arr[2]=8
-
输出第四次排序的结果:3,7,8,15,22
到此插入排序就讲解完了~~
以上是关于视频+图文+动画 详解插入排序(轻松易理解系列)的主要内容,如果未能解决你的问题,请参考以下文章
史上最易理解的快速排序原理详解以及Arrays.sort方法

