Eight HDU - 1043 (双向BFS)

Posted 2020-11-27 accepting

记得上人工智能课的时候老师讲过一个A*算法，计算估价函数(f[n]=h[n]+g[n])什么的，感觉不是很好理解，百度上好多都是用逆向BFS写的，我理解的逆向BFS应该是从终点状态出发，然后把每一种状态打表列举出来，最后O(1)查询就可以了。这种办法确实挺好，但是不会....。

这位大佬用的双向BFS https://blog.csdn.net/qq_41670466/article/details/84110090，挺好理解的，但是注释什么的比较少，也没有过多的介绍思路，所以我想借助这篇blog简单的介绍一下这个题目的双向BFS的思路。

双向BFS就是终点状态（从后向前）和起始状态（从前向后）一起寻找，当且仅当而且碰头时，就是答案了。

 

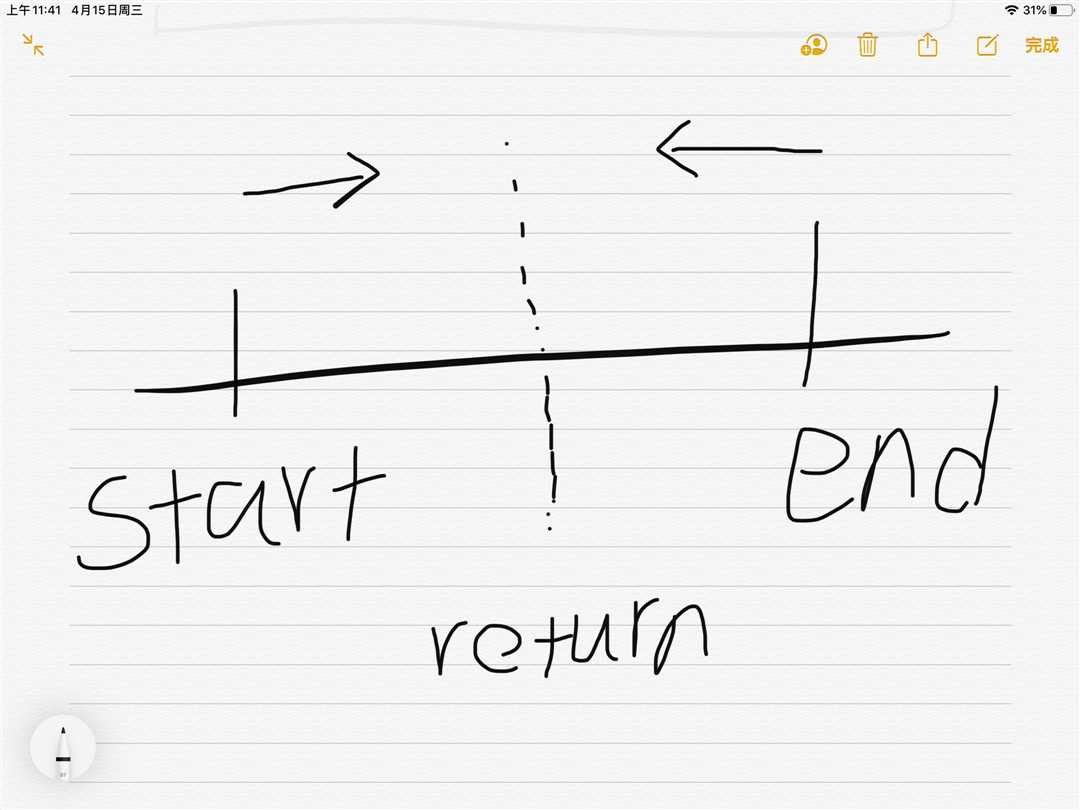
 针对本题来说，初始状态就是输入的转态，终点状态都是一样的123456780（x用0来代替），但是这个状态怎么表示呢？康托展开 （不会的可以点开看一下)。状态表示解决完了，接下来我们看一下转态转移。

当x处在0 3 6这三个位置时，不可以向左移动，当x处于2 5 8这三个位置时，不可以向右移动，当x处于0 1 2这三个位置时，不可以向上移动，处于6 7 8这三个位置时，不可以向下移动。 对于本题样例，s[]=2 3 4 1 5 x 7 6 8。，x是处于5这个位置，如果向上移动，就可以看成s[5]和s[5-3]交换了一下，向下移动可以看成s[5]和s[5+3]交换了一下，

向左s[5]和s[5-1]向右同理....这样就实现了状态之间的转移。

路径的记录。维护两个数组char 和int ,char 用来记录向哪移动了，int 用来记录上一个状态的下标。

最后还要加一个特判，问题是否有解跟逆序对有关，如果逆序对是奇数就有解，否则就无解具体为什么跟线性代数有关吧~~我也不太懂（待解释）。

具体实现都在code中了....

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+7;
string a;
int ha[10]={40320,5040,720,120,24,6,2,1,1};//从8到0对应的阶乘
int vis[maxn],vis2[maxn];
struct node {
    int num;
    char ch;
}pre[maxn];//write path
struct stu {
    string s;//当前串
    int num;//x的位置
}e;//save now state
int direction[]={-3,3,-1,1};//udlr
string s1="udlr",s2="durl";
int ct(string s){//当前串对应的康托值
    int sum=0;
    for(int i=0;i<9;i++){
        int k=0;
        for(int j=i+1;j<9;j++){
            if(s[j]>s[i]) k++;
        }
        sum+=k*ha[i];
    }
    return sum;
}
void writhpath(int x){
    if(pre[x].num==-1) return ;
    writhpath(pre[x].num);
    printf("%c",pre[x].ch);
}
void bfs(){
    queue<stu> que1,que2;
    int q=ct(e.s);
    vis[q]=1;
    stu f,g;
    f.s="123456780";
    f.num=8;
    int p=ct(f.s);
    vis2[p]=2;
    pre[1].num=-1;pre[2].num=-1;

    int num=2;
    que1.push(e);que2.push(f);
    while(que1.size()&&que2.size()){
        f=que1.front();que1.pop();
        p=ct(f.s);
        if(vis2[p]){
            writhpath(vis[p]);
            int k=vis2[p];
            while(pre[k].num!=-1) {
                printf("%c",pre[k].ch);
                k=pre[k].num;
            }
            cout<<endl;
            return ;
        }
        else{
            for(int i=0;i<4;i++){
               if(i==0&&f.num<3) continue ;
               if(i==1&&f.num>5) continue ;
               if(i==2&&f.num%3==0) continue ;
               if(i==3&&f.num%3==2) continue ;
               int dx=f.num+direction[i];g=f;
               swap(g.s[f.num],g.s[dx]);
               q=ct(g.s);
               if(vis[q]) continue ;
               vis[q]=++num;g.num=dx;
               que1.push(g);
               pre[num].num=vis[p];pre[num].ch=s1[i];
            }
        }
        f=que2.front();que2.pop();
        p=ct(f.s);
        if(vis[p]){
            writhpath(vis[p]);
            int k=vis2[p];
            while(pre[k].num!=-1) {
                printf("%c",pre[k].ch);
                k=pre[k].num;
           }
           cout<<endl;
           return ;
        }
        else{
            for(int i=0;i<4;i++){
               if(i==0&&f.num<3) continue ;
               if(i==1&&f.num>5) continue ;
               if(i==2&&f.num%3==0) continue ;
               if(i==3&&f.num%3==2) continue ;
               int dx=f.num+direction[i];g=f;
               swap(g.s[f.num],g.s[dx]);
               q=ct(g.s);
               if(vis2[q]) continue ;
               vis2[q]=++num;g.num=dx;
               que2.push(g);
               pre[num].num=vis2[p];pre[num].ch=s2[i];
            }
        }
    }
    puts("unsolvable");
}
int main(){
    while(getline(cin,a)){
        string c="";
        int n=a.size(),pos=0,j=0;
        for(int i=0;i<n;i++){
            if(a[i]==‘ ‘) continue ;
            if(a[i]==‘x‘){
                c+=‘0‘;pos=j;
            }
            else {
                c+=a[i];j++;
            }
        }
        int k=0;e.num=pos;e.s=c;
        for (int i=0;i<9;i++){
            if (e.s[i]==‘0‘)continue;
                for (int j = 0;j<i;j++){
                    if (e.s[j] == ‘0‘)continue;
                    if (e.s[j]>e.s[i])k++;
            }
        }
        if(k&1) {
             puts("unsolvable");
        }
        else {
            memset(vis,0,sizeof vis);
            memset(vis2,0,sizeof vis2);
            bfs();
        }
    }
    return 0;
}