二维取数dp

Posted 2020-11-27 1-0001

acwing 1027.方格取数

https://www.acwing.com/problem/content/1029/

对于走一次，容易得到状态转移方程为：$f[i][j] = max(f[i-1][j], f[i][j-1]) + w[i][j]$。

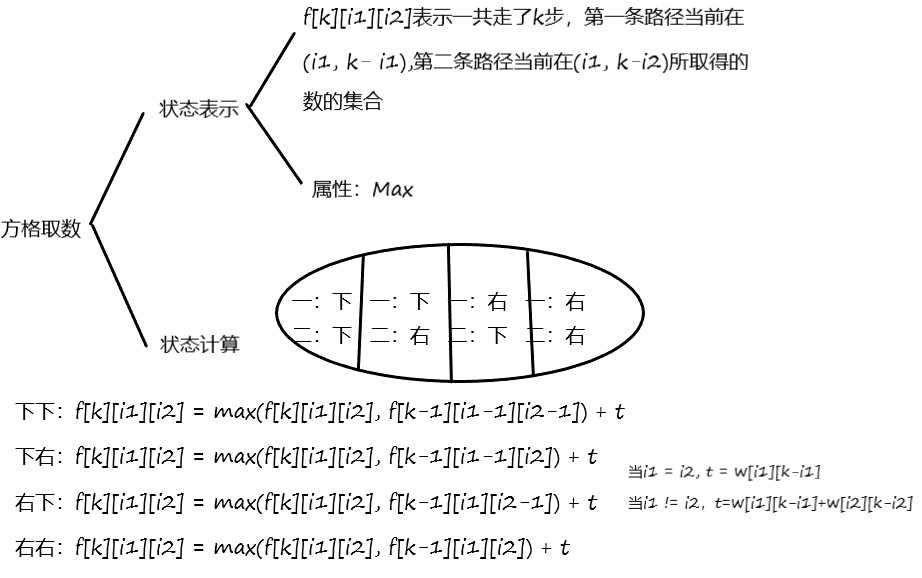
而对于走两次时，设定状态为$f[i_1][j_1][i_2][j_2]$表示第一条路径从$(1, 1)$走到$(i_1, j_1)$,第二条路径从$(1, 1)$走到$(i_2, j_2)$取的数的最大和。

该题的核心是：如何处理对于同一个格子不能取两次。分析可知，只有当$i_1 + j_1 = i_2+j_2$的时候，取的格子才有可能是同一个格子，这也启发我们可以将状态降一维。

用$k = i_1+j_1 = i_2+j_2$，这样状态就变成了$f[k][i_1][i_2]$。

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 15;
 7 
 8 int n;
 9 int w[N][N];
10 int f[N * 2][N][N];
11 
12 int main()
13 {
14     cin >> n;
15 
16     int a, b, c;
17     while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
18 
19     for (int k = 2; k <= n + n; k ++ )
20         for (int i1 = 1; i1 <= n; i1 ++ )
21             for (int i2 = 1; i2 <= n; i2 ++ )
22             {
23                 int j1 = k - i1, j2 = k - i2;
24                 if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
25                 {
26                     int t = w[i1][j1];
27                     if (i1 != i2) t += w[i2][j2];
28                     int &x = f[k][i1][i2];
29                     x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
30                     x = max(x, f[k - 1][i1 - 1][i2] + t);
31                     x = max(x, f[k - 1][i1][i2 - 1] + t);
32                     x = max(x, f[k - 1][i1][i2] + t);
33                 }
34             }
35 
36     cout << f[n + n][n][n] << endl;
37     return 0;
38 }