数据结构与算法：寻找峰值

Posted 2020-11-27 shitianfang

一维：

峰值规定：a[i]>a[i-1] and a[i]>a[i+1]，假定只存在一个峰值

1

2

1

9

5

0

 

 

例如9就是一个峰值

方法一：顺序遍历，时间复杂度O(n)

方法二：分治策略，将列表折半查找，第一次查找n/2，左右两边哪一边大继续折半查找哪一边

def search_peak(alist):
    l=0
    r=len(alist)-1
    while l<=r:
        mid=(l+r)//2
        if mid==0 or mid==len(alist)-1:
            return mid
        else:
            if alist[mid]<alist[mid-1]:
                r=mid-1
            elif alist[mid]<alist[mid+1]:
                l=mid+1
            else:
                return mid
    return -1
    
print(search_peak([1,1,1,1,1,2,3,5,7,9]))

这种写法并未考虑相邻两数相等情况的处理，并且只能处理查找一个峰值的情况，如果查找多个峰值，即使利用二分查找复杂度仍然会降为O(n)

时间复杂度分析：

1，首先进行一次折半得：T(n) = T(n/2) + O(1) 

2，n为剩余元素，O(1)代表进行一次比较

3，再次进行折半得：T(n) =  T(n/4) + O(1) *2

4，以此类推得：T(n) = T(n/2^k)+O(1)*k  #注意前面是幂，后面乘

5，令n/2^k=1（表示最后剩下一个元素）得：k=log2n

所以T(n) = O(1)*log2n = O(logn)

 

 二维：

	1
2	5	3
	4

 

 

 

 

长为m，宽为n

例如5就是一个峰值，通过算法找出来

方法一：贪婪上升算法，选择一个位置开始遍历，然后利用深度优先搜索一条路搜下去，最坏情况下时间复杂度是O(n*m)

方法二：分治策略：先二分求每一行的峰值，确定行峰值位置后，再判断它是不是大于列位置的相邻上下元素，时间复杂度为O(logn)

方法三：田字分割，时间复杂度O(n)

1，先找田字中最大的元素，此处为7

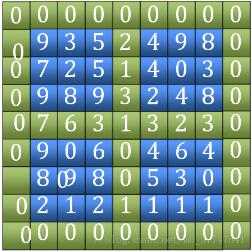
2，找到后判断是否为峰值，若不是，记录相邻四点中最大值的坐标，继续分割最大值坐标所在象限

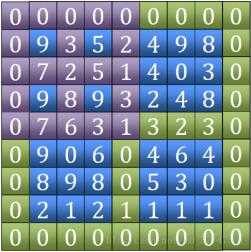
 3，当范围缩小到3*3时必定会找到局部峰值