单应矩阵
Posted yepeichu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了单应矩阵相关的知识,希望对你有一定的参考价值。
单应矩阵原理
单应(透射变换)是射影几何中的概念,又称为射影变换。他把一个射影平面上的点映射到另一个平面对应的位置,并且把直线映射为直线,具有保线性质。与对极几何不同的是,对极几何将点映射到线上,而单应矩阵是点对点的关系。要注意的是单应矩阵的适用场景为:当场景中的特征点都落在同一平面上,比如墙、地面等,此时可用单应性估计运动。
单应(透射变换)可以看成是仿射变换的拓展。仿射变换在图形中的变换包括:平移、缩放、旋转、斜切及它们的组合形式。这些变换的特点是:平行关系和线段的长度比例保持不变,即保持物体的平直性。而单应中也存在上述多种变换的组合形式,但是差别在于单应并不一定能保持平行关系和线段的长度比例不变。单应的特点是共面点成像,即单应变换是将某一块共面的地方变换到另外一个地方,但是多数情况下都会彻底改变物体位置和形状。
平面表示方法
首先需要确定一个平面法向量为 $mathbf{vec{n}} = [n_{1}, n_{2}, n_{3}]^{T}$,但是确定法向量并不能唯一确定一个平面。我们会得到无数多的相互平行的平面。为了唯一确定一个平面,我们还需要一个点,若平面上有一个定点 $mathbf{x} = [x_{1}, x_{2}, x_{3}]^{T}$, 那么我们即可确定一个平面。
    假设平面上任意一点为 $mathbf{m} = {x, y, z}$,平面方程为
$$Ax + By + Cz + D = 0$$
由于法向量已知,则上述方程可以表示成:
$$mathbf{vec{n}^{T}} mathbf{m} + D = 0$$
显然上述的方程表示的是无数组平行的平面,确定 $D$ 即可确定唯一平面。则利用上述所说的平面上的任意动点 $x$,则有:
$$D = -mathbf{vec{n}^{T}}mathbf{x} = -(n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3})$$
则平面的唯一表示方法为:
$$Ax + Bx + Cz = (n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3})$$
综上,为了表示一个平面,我们需要一个法向量,以及一个平面上的点(目的是为了求偏置)。
单应矩阵
由上述可知平面的表示方法可以写成:
$$mathbf{vec{n}}^{T}mathbf{x} = d$$
参考对极几何及单应矩阵这篇文章,我们可以得到单应约束图像:
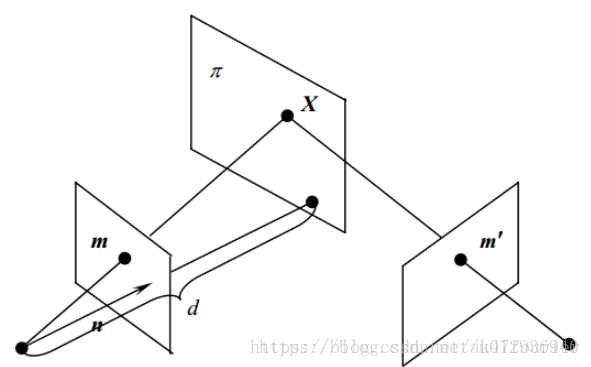
假设左边为第一个相机坐标系 $C_{1}$,右边为第二个相机坐标系 $C_{2}$。并且平面 $pi$ 在第一个相机坐标系的法向量为 $mathbf{vec{n}}$,$C_{2}$ 到平面 $pi$ 的距离为 $d$。假设平面中任意一个点 $mathbf{X}$ 在第一个相机坐标系中的表示为 $mathbf{X_{1}}$,则平面 $pi$ 的表示方法为:
$$mathbf{vec{n}}^{T} mathbf{X_{1}} = d$$
显然,上面的表示方法满足我们前面介绍的平面表示方法的约束条件,即一个法向量以及平面内有一个已知点。接着我们将平面 $pi$ 的表示方法改变一下:
$$frac{1}{d}mathbf{vec{n}}^{T} mathbf{X_{1}} = 1$$
假设平面 $pi$ 中有一空间点 $X$,对应两个相机的投影像素分别为 $mathbf{p_{1}}, mathbf{p_{2}}$,相机内参矩阵为 $mathbf{K},$归一化平面中的坐标系为 $mathbf{x_{1}},mathbf{{x_{2}}}$,并且满足条件 $s_{1}mathbf{x_{1}} = mathbf{X_{1}}$,其中 $s_{1}$ 为 $X_{1}$ 的深度值。若已知两个坐标系之间的相对变换为 $mathbf{R}, mathbf{t}$,表示从相机坐标系 $1$ 变换到相机坐标系 $2$,则有:
$$mathbf{x_{1}} = mathbf{K}^{-1}mathbf{p_{1}}$$
$$mathbf{x_{2}} = mathbf{K}^{-1}mathbf{p_{2}}$$
$$s_{2}mathbf{x_{2}} = s_{1}mathbf{R}mathbf{x_{1}} + mathbf{t}$$
$$s_{2}mathbf{K}^{-1}mathbf{p_{2}} = s_{1}mathbf{R}mathbf{K}^{-1}mathbf{p_{1}} + mathbf{t}$$
将平面 $pi$ 的信息代入上述方程中得到:
$$s_{2}mathbf{K}^{-1}mathbf{p_{2}} = s_{1}mathbf{R}mathbf{K}^{-1}mathbf{p_{1}} + frac{s_{1}}{d}mathbf{t}mathbf{vec{n}}^{T} mathbf{K}^{-1} mathbf{p_{1}} = s_{1}(mathbf{R} + frac{1}{d}mathbf{t}mathbf{vec{n}}^{T})mathbf{K}^{-1} mathbf{p_{1}} $$
两边左乘相机内参矩阵:
$$s_{2}mathbf{p_{2}} = s_{1} mathbf{K}(mathbf{R} + frac{1}{d}mathbf{t}mathbf{vec{n}}^{T})mathbf{K}^{-1} mathbf{p_{1}}$$
其中 $mathbf{H} = mathbf{K}(mathbf{R} + frac{1}{d}mathbf{t}mathbf{vec{n}}^{T})mathbf{K}^{-1}$ 称为单应矩阵。再进一步简化为:
$$mathbf{p_{2}} = frac{s_{1}}{s_{2}}mathbf{H}mathbf{p_{1}}$$
在上述的式子当中,我们发现除了单应约束以外,还有一个常系数 $frac{s_{1}}{s_{2}}$。实际上该系数影响并不大,因为在实际求解当中,我们需要将得到的三个方程同时除以第三个方程,才能得到两个有用的约束关系。(笔者以为:之所以需要这么做,是因为我们输入的数据,均是归一化的点,因此,在最终的结果上也应保持左右两边最后一维的数值应该为 $1$)。显然,上述方程对于尺度的变化是不敏感的,因为没有任何作用。
通过将约束条件 $mathbf{p_{2}} = mathbf{H}mathbf{p_{1}}$ 展开,我们可以得到两个方程。并且我们由上面的分析可以知道,单应矩阵 $mathbf{H}$ 并非是有 $9$ 维自由度的矩阵,因为其对尺度不敏感。所以我们将单应矩阵最后一维置为 $1$。(或者可以强制单应矩阵所有参数的平方和为 $1$)最后我们需要求解的单应矩阵一共有 $8$ 个维度。而每一对匹配点可以提供两个约束方程,那么我们至少需要四对匹配点才可以求解八个参数。在上一讲的对极约束中,我们求解的问题同样也是一个齐次方程。因此求解方法仍是采用SVD分解来得到。
拾遗
其实回顾上一讲中的本质矩阵,再关联一下基础矩阵。我们可以知道这两个矩阵之间相差的只是相机内参矩阵。而上述的单应矩阵其实也可以有两种解法。一种是如上的解法,也就是将相机内参矩阵融入问题结构中,与相机位姿一起求解,最后再分解出来,这种方法类对极约束中的基础矩阵的求法。另外一种就是去除相机内参,但是输入参数需要是归一化平面上的点,也就是说我们在第一步就将相机内参用了,无需再用它,那么求解单应矩阵的时候相应的就不需要求解相机内参了,这种方法类对极约束中的本质矩阵的求法。
由于OpenCV提供的求解函数是基于像素点的,因此单应矩阵中包含相机内参和相对位姿。为了能够和代码对得上,笔者就将内容修改为如上的内容。代码可以参考我的github。
参考材料
1. 对极几何及单应矩阵
2. 对极约束
3. 仿射变换与投影变换
以上是关于单应矩阵的主要内容,如果未能解决你的问题,请参考以下文章