题解看病

Posted 2020-11-27 5ab-juruo

题目描述

土匀匀最近身体不太舒服，他决定去看病，可是病在遥远的地方。土匀匀是个路痴，不知道该走什么路，于是他找到了学霸。

学霸这样说道：这里一共有 (n) 个城镇，城镇之间共有 (m) 条双向道路，每条道路有三个属性 (u_i)、(v_i) 和 (c_i)。(u_i) 和 (v_i) 表示它连接的城镇，(c_i) 表示费用。当土匀匀经过一个城镇的时候（包括起点和终点），费用为进入这个城镇的道路和出这个城镇的道路费用的较大值。

土匀匀想花最少的钱去看病，但他不会编程，于是他找到了聪明的你，希望你能帮他解决这个问题。

输入格式

输入的第一行是两个正整数 (n) 和 (m)，表示城镇的数目和道路的数目。（土匀匀在 (1) 号城镇，病在 (n) 号城镇，保证土匀匀一定能到达 (n) 号城镇）

接下来 (m) 行，每行三个正整数 (u_i)，(v_i)，(c_i)，意义如题面所述。

输出格式

输出只有一个整数，表示土匀匀要花的最少钱数。

数据范围

测试时间限制 (5000 mathrm{ms})，空间限制 (256 mathrm{MiB})。

• 对于 (30\%) 的数据，(2le nle 10)，(1le mle 10)；
• 对于 (50\%) 的数据，(2le nle 5000)，(1le mle 20000)；
• 对于 (100\%) 的数据，(2le nle 10^5)，(1le mle 2 imes 10^5)。

保证 (1le u_i,v_ile n)，(u_i eq v_i)，(1le c_ile 10^6)。

分析

此题十分毒瘤……代码敲了好几个小时啊。

但还是建议大家去敲一下，毕竟是一道好题。

(30 mathtt{pts})

怎么暴力怎么来。

(50 mathtt{pts})

有两种可行的做法：

第一种就是将每一条边视作一个节点，然后将两个新节点之间连一条边，权值为两端节点所对应的边的权值最大值。

这样建出来的新图就能直接跑最短路来解决了。

空间可能会被卡到 (mathcal{O}(m^2))。

---

第二种就是在跑最短路时，记录一下当前状态是从哪个节点来的。

这样，在松弛时，就可以计算当前边权了。

时间复杂度依旧堪忧。

(100 mathtt{pts})

满分做法是真的难想。

接下来，我会给大家梳理满分做法的方法、原因和思路。

---

首先，我们看到第一种做法，就是那个重新建图的做法。

这个做法的瓶颈就是在建边时，边的级别是 (mathcal{O}(m^2)) 的。

那么，我们怎么建边，才能让边的数量下降呢？

以下图举例：（注：为表示方便，没有标权值的边默认权值为 (0)。）

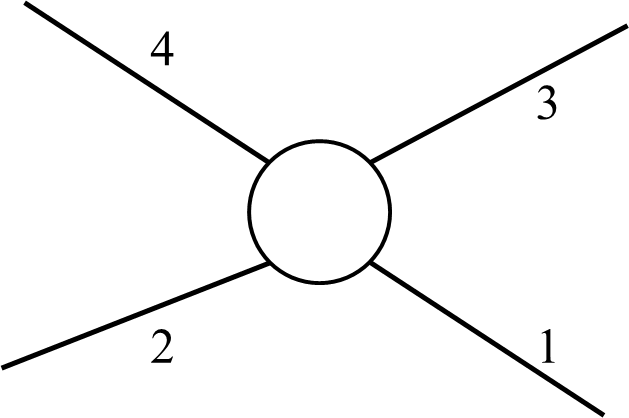
首先，作为边权最大的一条边，从这条边引出的所有路径都是以这条边的边权计算的。

那么，我们是不是可以考虑这样建边：

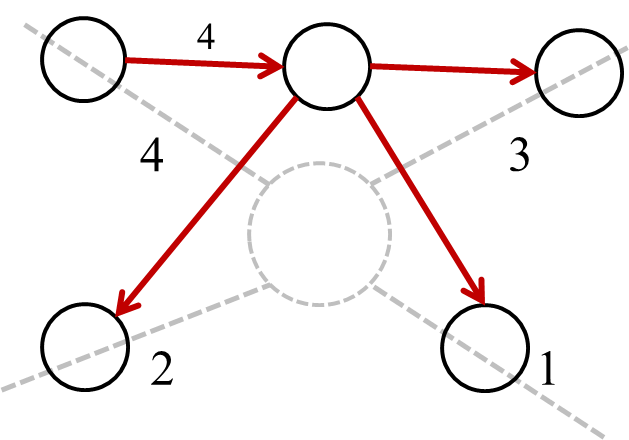
所以这有什么区别吗 (Qomega Q)

接下来考虑次大边。Ta 应该向所有比 Ta 小的边连边。

但是，我们的最大边要像次大边和所有比次大边小的边连边。那么，我们是不是可以这么操作：

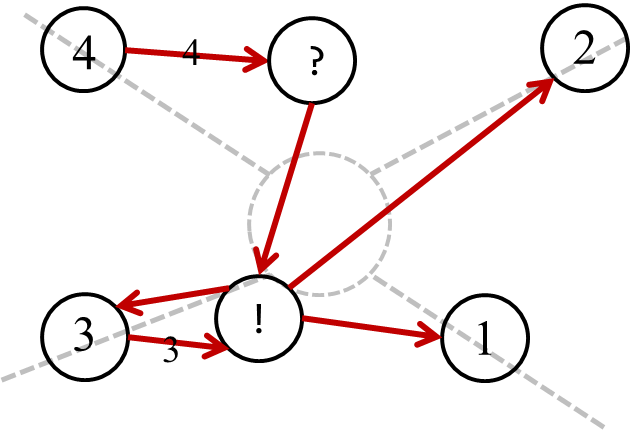
• 对于最大点，可以经过 ? 节点，再通过 ! 节点到达其他节点。
• 对于次大节点，可以直接通过 ! 节点到达比 Ta 小的节点。

这样，我们是不是可以省掉很多边呢？

如此这般，我们就可以这么建图：

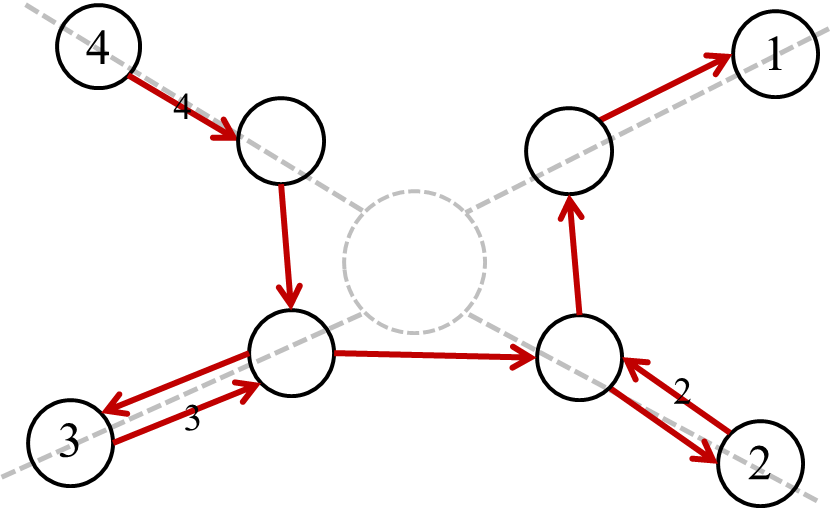
复杂度？

每条边来回，一个环，妥妥的 (Theta(m))。

---

？？？等等，题目中不是说是双向边吗，怎么是这样啊？不是单向的吗？

莫急，我们先把反向的图建好。

注意一下反向后权值的位置。否则就会不对了。

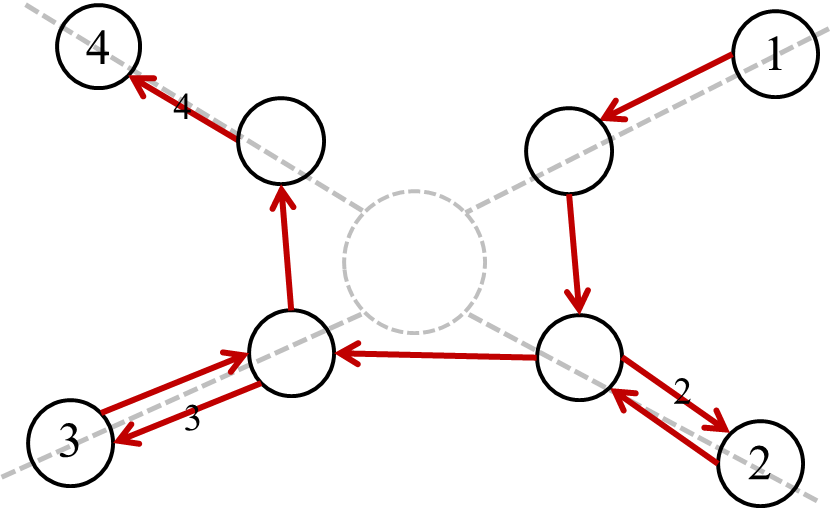
？？？你莫不是把原图中的边反过来了？别骗我！

确实是正好反过来了，但是就是这么画的啊。不信你试试 (Qomega Q)。

---

好了，这样有了两张图，又怎么办呢？不是说好一张图的吗？

很简单，只要将两张图中节点相同的部分合并，就是可以的啦。

但是，那几个中间节点不能合并。因为那些节点代表着不同的方向和大小关系。

接下来就是愉悦的最短路环节啦，撒花~~ ??ヽ(°▽°)ノ?。

咳咳，我们还没算过复杂度嘞，撒啥花。

时间复杂度主要是最短路，而新图中边的数量不超过原图的 (12) 倍，是 (Theta(m)) 的，所以最终复杂度是 (Theta(mlog m))（常数取决于最终的代码实现，如果是用 Fibonacci 堆优化 Dijkstra，那么可以很小；但是如果是堆优化 Dijkstra，就很容易跑满）。

Code

又是一个代码量 (200) line+ 的题目啊……

#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
using namespace std;

#define FRONT_SMALLER 0
#define FRONT_BIGGER 1
#define BACK_SMALLER 2
#define BACK_BIGGER 3
#define CENTER 4

typedef long long ll;
const int max_n = 100000, max_m = 200000;

struct st_t
{
	int val, id;
	
	bool operator<(const st_t& a) const { return val < a.val; }
};

struct hp_elem
{
	int id;
	ll val;
	
	hp_elem(int _i = 0, ll _v = 0) : id(_i), val(_v) { }
	
	bool operator<(const hp_elem& k) { return val < k.val; }
};

class heap
{
	private:
		
		hp_elem s[max_m*5+1];
		int len;
		
		inline int lson(int id) { return id << 1; }
		inline int rson(int id) { return (id << 1) | 1; }
		inline int par(int id) { return id >> 1; }
		inline void swap(int id) { hp_elem tmp = s[id]; s[id] = s[par(id)], s[par(id)] = tmp; }
	
	public:
		
		heap() : len(0) { }
		
		void insert(hp_elem n)
		{
			s[++len] = n;
			int p = len;
			
			while (p != 1 && s[p] < s[par(p)])
			{
				swap(p);
				p = par(p);
			}
		}
		
		hp_elem query() const { return s[1]; }
		bool is_empty() const { return !len; }
		
		void remove()
		{
			s[1] = s[len--];
			int p = 1, t;
			
			while (rson(p) <= len)
			{
				if (s[lson(p)] < s[rson(p)])
					t = lson(p);
				else
					t = rson(p);
				
				if (s[t] < s[p])
				{
					swap(t);
					p = t;
				}
				else
					return;
			}
			
			if (lson(p) <= len && s[lson(p)] < s[p])
				swap(lson(p));
		}
};

namespace ZBSAKIOI
{
	int hd[max_n+2], des[(max_m+2)<<1], val[(max_m+2)<<1], nxt[(max_m+2)<<1], edge_cnt = 0;
	
	void add_edge(int s, int t, int v)
	{
		des[edge_cnt] = t, val[edge_cnt] = v;
		nxt[edge_cnt] = hd[s], hd[s] = edge_cnt++;
	}
}

st_t tmp[max_m];
heap hp;

int hd[max_m*5+10], des[max_m*12+24], val[max_m*12+24], nxt[max_m*12+24], edge_cnt = 0;
ll dis[max_m*5+10];
bool vis[max_m*5+10] = {};

inline int read()
{
	int ch = getchar(), n = 0, t = 1;
	while (isspace(ch)) { ch = getchar(); }
	if (ch == ‘-‘) { t = -1, ch = getchar(); }
	while (isdigit(ch)) { n = n * 10 + ch - ‘0‘, ch = getchar(); }
	return n * t;
}

inline int get_id(int p_id, int n_id) { return p_id * 5 + n_id; }

void add_edge(int s, int t, int v)
{
	des[edge_cnt] = t, val[edge_cnt] = v;
	nxt[edge_cnt] = hd[s], hd[s] = edge_cnt++;
}

int main()
{
	memset(ZBSAKIOI::hd, -1, sizeof(ZBSAKIOI::hd));
	memset(hd, -1, sizeof(hd));
	memset(dis, 0x3f, sizeof(dis));
	
	int n = read(), m = read(), ta, tb, tc, st, ed;
	hp_elem cur;
	
	for (int i = 0; i < m + 2; i++)
	{
		if (i < m)
			ta = read() - 1, tb = read() - 1, tc = read();
		else if (i == m)
			ta = n, tb = 0, tc = 0;
		else
			ta = n - 1, tb = n + 1, tc = 0;
		
		ZBSAKIOI::add_edge(ta, tb, tc);
		ZBSAKIOI::add_edge(tb, ta, tc);
		
		add_edge(get_id((ZBSAKIOI::edge_cnt - 1) >> 1, CENTER), get_id((ZBSAKIOI::edge_cnt - 1) >> 1, BACK_BIGGER), tc);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 1) >> 1, CENTER), get_id((ZBSAKIOI::edge_cnt - 1) >> 1, BACK_SMALLER), 0);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 1) >> 1, BACK_BIGGER), get_id((ZBSAKIOI::edge_cnt - 1) >> 1, CENTER), 0);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 1) >> 1, BACK_SMALLER), get_id((ZBSAKIOI::edge_cnt - 1) >> 1, CENTER), tc);
		
		add_edge(get_id((ZBSAKIOI::edge_cnt - 2) >> 1, CENTER), get_id((ZBSAKIOI::edge_cnt - 2) >> 1, FRONT_BIGGER), tc);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 2) >> 1, CENTER), get_id((ZBSAKIOI::edge_cnt - 2) >> 1, FRONT_SMALLER), 0);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 2) >> 1, FRONT_BIGGER), get_id((ZBSAKIOI::edge_cnt - 2) >> 1, CENTER), 0);
		add_edge(get_id((ZBSAKIOI::edge_cnt - 2) >> 1, FRONT_SMALLER), get_id((ZBSAKIOI::edge_cnt - 2) >> 1, CENTER), tc);
	}
	
	for (int i = 0; i < n + 2; i++)
	{
		tc = 0;
		for (int p = ZBSAKIOI::hd[i]; p != -1; p = ZBSAKIOI::nxt[p], tc++)
			tmp[tc].val = ZBSAKIOI::val[p], tmp[tc].id = p;
		
		sort(tmp, tmp + tc);
		
		if (i == n)
			st = get_id(tmp[tc-1].id >> 1, ((tmp[tc-1].id - (tmp[tc-1].id >> 1 << 1)) << 1) + 1);
		else if (i == n + 1)
			ed = get_id(tmp[0].id >> 1, ((tmp[0].id - (tmp[0].id >> 1 << 1)) << 1) + 1);
		
		for (int i = 1; i < tc; i++)
		{
			ta = tmp[i-1].id, tb = tmp[i].id;
			add_edge(get_id(ta >> 1, (ta - (ta >> 1 << 1)) << 1), get_id(tb >> 1, (tb - (tb >> 1 << 1)) << 1), 0);
			add_edge(get_id(tb >> 1, ((tb - (tb >> 1 << 1)) << 1) + 1), get_id(ta >> 1, ((ta - (ta >> 1 << 1)) << 1) + 1), 0);
		}
	}
	
	dis[st] = 0;
	hp.insert(hp_elem(st, 0));
	
	while (!hp.is_empty())
	{
		cur = hp.query();
		hp.remove();
		
		if (!vis[cur.id])
		{
			vis[cur.id] = true;
			
			for (int p = hd[cur.id]; p != -1; p = nxt[p])
				if (dis[des[p]] > dis[cur.id] + val[p])
				{
					dis[des[p]] = dis[cur.id] + val[p];
					
					if (!vis[des[p]])
						hp.insert(hp_elem(des[p], dis[des[p]]));
				}
		}
	}
	
	printf("%lld
", dis[ed]);
	
	return 0;
}

后记

这篇题解的主体内容是 5ab 在看完报告后脑补出来的，希望大家能够看懂且有耳目一新的感觉。

5ab 希望自己的题解能够比较自然，不会有奇怪的想法之类的。这篇题解也是秉承着这样的理念去写的。

如果你有自己的见解，欢饮留下你的言论。