Codeforces 1316C - Primitive Primes

Posted 2020-11-26 stelayuri

（好久没打cf了，晚上没啥事随便补了一题，毕竟咕咕咕了这么久）

本篇主要证明题目结论的原理，所以才写了这么多字

 

题目大意：

给定两个多项式长度 n 和 m ，再给定每一项的系数，由常数项到最高次项

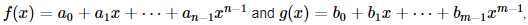
保证多项式所有项系数的最大公约数为 1

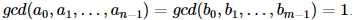
再给定一个质数 p

问两个多项式相乘后得到的第三个多项式中

哪一项的系数不是 p 的倍数，输出这个项的x的幂次（下标）

存在多个答案时，输出任意一个

 

解题思路：

从 “保证多项式所有项系数的最大公约数为 1” 可得题目一定有解（反正没说无解的输出情况略略略）

根据x的次数关系可以得到第三个多项式的系数表达式为

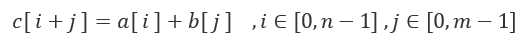
求的是满足 c[ t ] % p != 0 时 t 的值

首先知道的是，p 是个质数

只有两个数 α 和 β 同时满足 α mod p ≠ 0 并且 β mod p ≠ 0 时

那么两数之积 α*β mod p ≠ 0 才成立

相反，只要有一个数不满足 mod p ≠ 0 ，那么乘法就相当于多个这个数相加，明显后者结论不成立

所以我们要在 a 数列和 b 数列中找不是p倍数的数出现的位置

假设找到在 a 数列中位置 i 的数和 b 数列中位置 j 的数满足条件

那么对应在 c 数列中的位置为 i+j

但是需要注意，有可能目前 a[ i ]*b[ j ] %p 不等于0，但是 c 数列的表达式是一个多项式，有可能其他项 %p 后与我们找到的 a[ i ]*b[ j ]%p 得到的值正好凑成了p，这样的话这个 i+j 无法成为答案

所以，我们需要保证 c 数列中 i+j 这个位置，除了 a[ i ]*b[ j ] 这一项以外，其他项不能出现 %p ≠ 0 的情况（事实上出现是可以出现的，只要保证取模后相加不是p的倍数即可，但是处理起来很麻烦，又因为两个数列中一定存在某些项不是p的倍数，所以这里直接贪心）

想到的只有以下两种情况能够保证：

　　①：i 和 j 这两个位置的数分别是 a 数列和 b 数列中第一个出现的不是 p 倍数的数

　　②：i 和 j 这两个位置的数分别是 a 数列和 b 数列中最后一个出现的不是 p 倍数的数

证明①：

c[ i+j ] 的构成为 ...+ a[ i-1 ]*b[ j+1 ] + a[ i ]*b[ j ] + a[ i+1 ]*b[ j-1 ] +...

因为 i 是 a 数列中第一个出现的不是 p 倍数的数

所以 a[ i-1 ] , a[ i-2 ] ,... 都是 p 的倍数，与任何数相乘都还是p的倍数，所以左边划掉

因为 j 是 b 数列中第一个出现的不是 p 倍数的数

所以 b[ j-1 ] , b[ j-2 ] ,... 都是 p 的倍数，与任何数相乘都还是p的倍数，所以右边划掉

只剩下中间一项不是 p 的倍数了，i+j 能够成为答案

证明②：

c[ i+j ] 的构成为 ...+ a[ i-1 ]*b[ j+1 ] + a[ i ]*b[ j ] + a[ i+1 ]*b[ j-1 ] +...

因为 i 是 a 数列中最后一个出现的不是 p 倍数的数

所以 a[ i+1 ] , a[ i+2 ] ,... 都是 p 的倍数，与任何数相乘都还是p的倍数，所以右边划掉

因为 j 是 b 数列中最后一个出现的不是 p 倍数的数

所以 b[ j+1 ] , b[ j+2 ] ,... 都是 p 的倍数，与任何数相乘都还是p的倍数，所以左边划掉

只剩下中间一项不是 p 的倍数了，i+j  能够成为答案

 

代码很简单，主要是证明……（966ms / 1500ms）

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int main(){
 4     ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
 5     int n,m,p,i,d,p1=-1,p2=-1;
 6     cin>>n>>m>>p;
 7     for(i=0;i<n;i++){
 8         cin>>d;
 9         if(d%p/* &&p1!=-1 */)//可加可不加，加了就是取第一项，不加取最后一项
10             p1=i;
11     }
12     for(i=0;i<m;i++){
13         cin>>d;
14         if(d%p/* &&p2!=-1 */)
15             p2=i;
16     }
17     cout<<p1+p2<<‘
‘;
18     
19     return 0;
20 }

题外话：

代码简单归简单，但是数据好像有点多，这点代码量跑了近 2/3 的时限

于是我开了下io外挂

……

没错，程序用时暂时全服第一了（划掉）（78ms）

但这不重要，开心就好